行星传动系统啮合振动信号的传递路径分析

黄奕宏，何国林，曾智杰

(华南理工大学机械与汽车工程学院，广州 510640)

行星齿轮传动系统的噪声和振动控制一直是各学者研究和关注的焦点。在许多应用场合，行星齿轮传动系统的振动和噪声是影响系统可靠性、寿命及操作环境的关键因素［1］。美国国家航空航天局在一次常规的检测中，意外发现美国“黑鹰”直升机行星齿轮箱中行星架上出现裂纹，严重影响飞行安全［2］。丹麦某公司的风电齿轮箱所出现的齿轮故障令商业在线监测与诊断系统束手无策，而传统的信号处理方法对此又无能为力，最终造成严重的经济损失［3］。

Inalploat等［4－5］对齿轮箱进行分类并分析其频谱特征，提出了行星齿轮传动系统非线性时变动态模型，并通过模型预测了齿轮加工误差所产生的调制边频带。冯志鹏等［6－8］对齿轮箱振动信号方程式进行了展开分析，对行星齿轮箱的频谱特征进行了公式求解，研究在不同故障下的行星齿轮箱频谱特征及解调方法。

目前在关于行星齿轮箱的研究中，当考虑行星齿轮箱振动信号受传递路径影响时，所使用的汉宁窗函数仅描述了靠近传感器的齿圈圆周与行星轮啮合所产生的振动信号，而对其他圆周上的啮合振动信号置零［4，6］，无法准确、客观地描述啮合振动信号的传递路径影响。

本研究基于Virtual.Lab设计了一个行星齿轮箱壳体有限元模型，利用傅氏级数展开式及Matlab曲线拟合工具推导出行星传动系统啮合振动信号的传递路径数学模型。

1 啮合振动信号的传递路径影响

在行星齿轮箱中，齿圈一般固定不动，太阳轮、行星轮和行星架旋转，传感器通常安装在齿圈或与之相连的箱体上。如图1所示，以行星轮数N=3为例，1，2，3分别代表3个行星轮，R为齿圈周长的1/N，齿圈固定，传感器安装于齿圈正上方。在这种情况下，太阳轮与行星轮的啮合振动信号先通过太阳轮传递至太阳轮轴，再由太阳轮轴通过齿轮箱壳体传递至传感器。在齿轮箱的工作过程中，该路径不受行星轮公转的影响。行星轮与齿圈的啮合振动信号直接通过齿轮箱壳体传递至传感器。当行星轮公转时，啮合点至传感器的距离发生变化，导致啮合振动信号的传递路径也发生变化。当行星轮公转至靠近传感器时，其啮合点也靠近传感器，此时的啮合振动信号强度最大;在行星轮公转至远离传感器的过程中，其信号强度越来越弱。

图1 行星齿轮箱二维简图

目前所建立的行星齿轮箱振动信号方程式考虑了行星轮公转至R弧段内的齿轮啮合振动信号，并用汉宁窗函数来表示［4］。在实际工作中，整个齿圈圆周与行星轮的啮合振动信号均会传递至传感器，其幅值变化规律也不能简单地用窗函数的形式来描述。

2 行星齿轮箱壳体有限元仿真分析

表1为齿轮箱壳体有限元模型的材料属性。对图2有限元模型进行模态仿真分析，图中箭头所指方向为仿真分析中的激励力作用点，序列1～7为仿真分析中的加速度响应点。通常情况下，传感器在使用中所采集的振动加速度信号方向多为垂直于齿轮箱壳体轴向，因此仿真分析取垂直于地面约束的+Y方向。

表1 齿圈有限元模型材料属性

通过有限元仿真分析可以得出各响应点到激励点的幅频函数及相频函数，如图3，4所示。从图3可以看出:在齿圈壳体圆周上，虽然在任意频率下各响应点到齿圈上方激励点的频响幅值均随着响应点到激励点的距离增大而变小，但是在距离传感器最远端的第7响应点，其频响幅值仍然不为0。从图4可以看出:在齿轮箱壳体1阶固有频率内，各响应点的频响相位基本一致。

图2 行星齿轮箱壳体Virtual.Lab有限元模型

图3 齿轮箱壳体有限元模型幅频函数

图4 齿轮箱壳体有限元模型相频函数

该齿轮箱壳体结构对称，且材料属性均匀，因此Y轴上的对称点频响幅值视为相同。在任一频率下对整个齿轮箱壳体的频响幅值做拟合，结果如图5所示，其中点8～12分别为点6～2在Y轴上的对称响应点，从第1至第12点描绘了整个齿轮箱壳体的轮廓。当行星轮公转至第12点后，重新回到了第1点，每两条曲线频率间隔为1 Hz。

图5 有限元仿真幅频函数三维图(1～2 500 Hz)

3 传递路径变化规律的数学建模

以齿轮箱壳体中心为原点建立极坐标，用傅氏级数展开式(1)对壳体上离散点做拟合，可以近似得出整个齿圈圆周在任一啮合频率下的振动信号传递幅值变化曲线，其中m为傅氏级数展开式的拟合级数。分别取啮合频率fm为1 000和2 000 Hz时的频响幅值做拟合。表2为在两种不同啮合频率下各响应点的频响幅值。表3为拟合级数与均方根误差的关系，从表中可以看出，随着拟合级数的增加，拟合精度越高。两种啮合频率下的频响幅值拟合曲线如图6和图7所示。

式中:γ为角变量;以齿圈1响应点为起点，整个齿圈圆周为2π;a0和an为各展开式系数。

表2 不同啮合频率下各响应点的频响幅值

表3 傅氏级数拟合均方根误差

图6 傅氏级数展开式拟合曲线(1 000 Hz)

图7 傅氏级数展开式拟合曲线(2 000 Hz)

将式(1)中的角变量转换为时间变量，假设行星架转频为fc，第i个行星轮的第1阶起始相位为θi，将 γ =2πfct+θi代入式(1)中，同样可以用傅氏级数展开式表示第i个行星轮在整个齿圈圆周的振动信号传递幅值变化曲线:

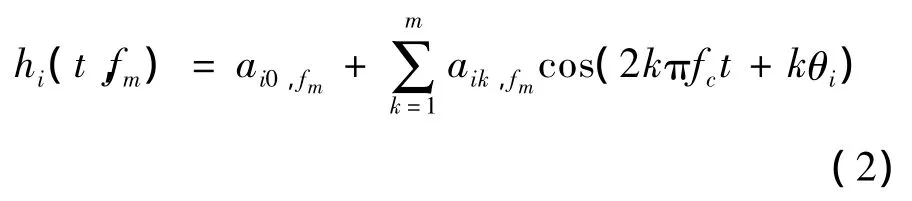
式中:ai0，fm和 aik，fm与齿轮箱壳体的结构与材料属性、约束条件有关;θi为第i个行星轮的第1阶起始相位，i=1，2，…，N(N为行星轮数)。当规定的第1个行星轮和齿圈的啮合点处于啮合振动信号传递幅值的最大点时，相位θi=0。

4 结束语

根据行星传动系统的实际工作状况，完整地考虑整个齿圈壳体与行星轮啮合所产生的啮合振动信号，运用有限元仿真分析得出齿圈壳体上各离散点的频响函数，利用傅氏级数展开式和曲线拟合工具对任一频率下的壳体频响幅值做拟合，得到了高精度的数学模型。此外，所推导的高阶数学模型完整地描述了整个齿圈圆周的幅值变化规律，而并非简单的汉宁窗函数。该数学模型为行星齿轮箱的数学建模提供了更加精确的理论支持。

［1］PARKER R G，AGASHE V，VIJAYAKAR S M.Dynamic response of a planetary gear system using a finite element/contact mechanics model［J］.ASME，Journal of Mechanical Design，2000，122(9):304－310.

［2］PATRICK R，ORCHARD M E，ZHANG Bin，et al.An integrated approach to helicopter planetary gear fault diagnosis and failure prognosis［C］//42nd Annual Systems Readiness Technology Conference.Baltimore，Maryland，USA:［s.n.］，2007:547－552.

［3］BARSZCZ T，RANDALL R B.Application of spectral kurtosis for detection of a tooth crack in the planetary gear of a wind turbine［J］.Mechanical Systems and Signal Processing，2009，23(4):1352－1365.

［4］INALPOLAT M，KAHRAMAN A.A theoretical and experimental investigation of modulation sidebands of planetary gear sets［J］.Journal of Sound and Vibration.2009，323(4):677－696.

［5］INALPOLAT M，KAHRAMAN A.A dynamic model to predict modulation sidebands of a planetary gear set having manufacturing errors［J］.Journal of Sound and Vibration，2010，329(4):371－393.

［6］Zhipeng Feng，Ming J.Fault diagnosis of planetary gearboxes via torsional vibration signal analysis［J］.Mechanical Systems and Signal Processing，2013，36:401－421.

［7］冯志鹏，赵镭镭，褚福磊.行星齿轮箱齿轮局部故障振动频谱特征［J］.中国电机工程学报，2013，33(5):119－127.

［8］冯志鹏，褚福磊.行星齿轮箱故障诊断的频率解调分析方法［J］.中国电机工程学报，2013，33(11):112－117.