超声相控阵探头指向性优化算法研究
2015-12-05郑浩鑫郑智贞刘杏娟黄明辉湛利华朱自清刘立达
郑浩鑫,郑智贞,刘杏娟,黄明辉,湛利华,朱自清,刘立达
(1.中南大学 机电工程学院,湖南 长沙 410083;2.中北大学 机械与动力工程学院,山西 太原 030051;3.中北大学 仪器与电子学院,山西 太原 030051;4.豫西工业集团有限公司,河南 南阳 471002)
超声相控阵探头指向性优化算法研究
郑浩鑫1,2,郑智贞2,刘杏娟3,黄明辉1,湛利华1,朱自清3,刘立达4
(1.中南大学 机电工程学院,湖南 长沙 410083;2.中北大学 机械与动力工程学院,山西 太原 030051;3.中北大学 仪器与电子学院,山西 太原 030051;4.豫西工业集团有限公司,河南 南阳 471002)
以典型的超声相控一维阵列探头为研究对象,从其声束指向性函数入手,分析了超声相控一维阵列探头的阵元中心距在消除栅瓣方面的作用,总结了阵元中心距的最佳取值范围,为相控阵探头的设计和性能优化提供了依据和参考。
超声相控阵;声学指向性;一维阵列探头;参数优化
0 引言
阵列式超声探头又称为超声相控阵探头,是根据压电晶体的逆向压电效应原理,将一系列压电元件按一定规则排成一个阵列,它不仅可增强超声波的辐射强度,更重要的是可结合现代计算机控制技术、嵌入式系统以及FPGA技术等进行相位控制,进而改变指向特性,更好地实现“精确聚焦”[1]。
本文将从一维阵列声场空间的声束指向性公式入手,对超声阵列探头中的声束指向性参数进行研究,为复杂相控阵探头的设计和优化提供相关依据和参考。
1 一维线性阵列超声相控阵探头的指向性函数
多个压电晶片按一定模式组成一体,按其阵列结构的不同,超声相控阵探头可分为一维阵列、二维阵列、环形阵列等类型[2],如图1所示。
一维阵列相比二维阵列、环形阵列和扇形阵列,具有结构简单、成本较低的特点,同时不失典型性[3],所以本文从一维线性阵列超声相控阵探头的指向性函数入手,分析其声场特性[4]。

图1 常见的阵列类型
本文研究时不考虑阵列位置的影响。假设有N个简谐点声源(阵元),其幅度A、角频率ω均相同,相位差δ逐次增加。当这N个点声源同时作用于空间中某点时,根据惠更斯原理,各声源将在这点叠加,形成干涉效应,在这点处产生的声压P可表示为:
P=Acos(ωt)+Acos(ωt+δ)+…+Acos[ωt+(N-1)δ]=

(1)
在超声相控阵探头中,可通过软件编程[6]的方法对各阵元进行“相移”或时间延迟,达到对各阵元的相位进行精确控制的目的,从而改变声束的指向性。但是由于排成一个阵列的一系列声辐射单元在空间某点“声程”的不同,也会导致各阵元的相位差,所以在超声相控阵探头设计中,必须考虑与指向性有关的阵列参数的影响,并且予以优化,以达到最佳的相位控制效果[7]。
图2为一维阵列声波叠加示意图。阵元沿X轴方向等距排列,各阵元间距为d,共N个,第i个阵元距空间点(x,y,z)的距离为ri,各阵元发射的声束和X轴及Z轴的夹角均为α和θ,为了计算的方便,令α和θ相等。

图2 一维阵列声波叠加示意图
根据惠更斯原理,各阵元辐射的声波压力Pi会在空间中某点(x,y,z)处叠加,倘在ri≥d的远场条件下,声线可看作一束平行线,此时可认为各阵元的方向矢量相同、发射灵敏度一致,故声波幅度一致,在叠加时可使结果显著简化,并用波长λ表示,即:

(2)
其中:P(d,α,θ)为合成声压;Ψ为空间中某点(x,y,z)处声波的相位。
由式(2)可以知道,合成声压P(d,α,θ)在某一方向(αm,θm)必然存在最大值,在这个最大值处的波束称为主波束,其声压表示为Pm(d,αm,θm)。
定义指向性函数H(θ):

(3)
将声线单位矢量和主波束单位进行矢量合成,可使H(θ)用H1(θ)和H2(θ)表示,即:

(4)
在式(4)中,不妨假定αm、α皆为0,则H2(θ)可化简为:

(5)
当相控阵指向性函数H2(θ)=1时,此时极角θ所在的波束有主瓣和栅瓣。当i=0时,θ0所在的波束称为主瓣;当i=1,2,…,N-1时,θi所在的波束称为第i个栅瓣,栅瓣是幅值为1的除主瓣外的旁瓣。
栅瓣的出现意味着声波在除了控制角方向上的其他地方也有传播,即声能有泄漏。栅瓣的存在,因其幅值几乎和主瓣相同从而会产生误判,因此必须准确定位栅瓣的位置并尽量消除栅瓣,从而达到声束指向性优化的目的。
2 探头的声束指向性参数优化
衡量超声相控阵探头指向性好坏的主要标准为主瓣宽度、有无栅瓣和旁瓣幅度[8]。声束指向性优化主要指减小主瓣宽度、消除栅瓣和使旁瓣幅度最小化。
栅瓣的存在不仅会造成严重的能量泄漏,甚至会造成缺陷位置的误判,使探头分辨能力降低,故栅瓣必须完全除去。因栅瓣是幅值为1的除主瓣外的旁瓣,故H2(θ)=1,即:

(6)
由式(6)可知,πd(sinθm-sinθ)/λ=±nπ(n=0,1,2…,N-1)。
则极角θn为:
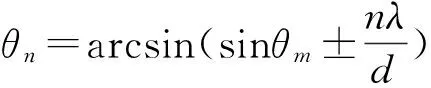
(7)
除n=0时,θ0为主瓣偏转角外,θn为第n级栅瓣所在的波束角。为了将其所在波束的栅瓣完全消除,取H2(θ)的极小值,即πd(sinθm-sinθ)N/λ=±nπ时,可得到消除栅瓣的条件:
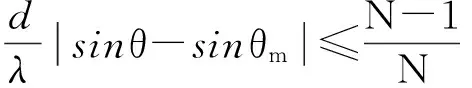
(8)
如果波束在±90°内偏转且不出现栅瓣时,令θ=±90°,将式(8)化简为:

(9)
式(9)即为消除栅瓣的条件。
在阵元中心距d确定的情况下,不产生栅瓣的最大偏转角θm为:

(10)
结合消除栅瓣的条件,可得d的取值范围:
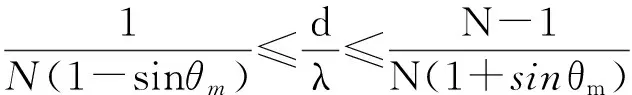
(11)
故阵元间距d在式(11)范围内取值可消除栅瓣。
3 结束语
分析研究了探头的阵元中心间距d和偏转角度θ对一维超声相控阵探头声束指向性的影响,主要探讨了这些参数对消除栅瓣的影响,为超声相控阵探头的优化设计提供理论指导和依据。在超声相控阵探头设计时除考虑压电材料、阻尼材料和吸声材料的选择以外,还需综合考虑阵元各参数的相互影响,以获得最佳的声束指向性。
[1] 钟志民,梅德松.超声相控阵技术的发展与应用[J].无损检测,2002,24(2):67-69.
[2] 冯若.超声手册[M].南京:南京大学出版社,1999.
[3] 李雯雯.超声相控阵技术的声场模拟和实验系统研究[D].济南:山东师范大学,2011:30-35.
[4] 郑晖,林树青.超声检测[M].北京:中国劳动社会保障出版社,2008.
[5] 宋志明,王黎,周小红,等.超声相控阵技术中的声场仿真[J].压电与声光,2012(4):567-569.
[6] 刘晨,魏伟.超声数字式相控阵列换能器动态聚焦系统研制[J].应用声学,2000,19(6):15-16.
[7] 何汶静,祝元仲,王宇峰,等.相控阵超声探头声场的建模与仿真[J].生物医学工程学杂志,2012,29(5):62-65.
[8] 黄晶,周社育,阙沛文.线性超声相控换能器阵列的参数优化[J].压电与声光,2010(2):52-53.
Directivity Optimization Algorithm Design of Ultrasonic Phased Array Probe
ZHENG Hao-xin1,2, ZHENG Zhi-zhen2, LIU Xing-juan3, HUANG Ming-hui1, ZHAN Li-hua1, ZHU Zi-qing3, LIU Li-da4
(1.School of Mechanical and Electronical Engineering, Central South University, Changsha 410083, China;2.School of Mechanics and Power Engineering, North University of China, Taiyuan 030051, China;3.School of Instrument and Electronics, North University of China, Taiyuan 030051, China;4.The Western Industrial Group Co., Ltd., Nanyang 471002, China)
This paper took a one-dimensional ultrasonic phased array probe as an example, began from the beam directivity function, analyzed the influence of the center distance of one-dimensional ultrasonic phased array probe on eliminating the grating lobe, and pointed out the best value range of the center distance. The results could be used as a good reference basis for the design of phased array probe and its performance optimization.
ultrasonic phased array probe; beam directivity; one-dimensional array probe; parameter optimization
1672- 6413(2015)06- 0017- 02
2015- 01- 26;
2015- 09- 10
郑浩鑫(1979-),男,河北张家口人,讲师,硕士,研究方向:测试计量技术与仪器。
TN919.6+3
A
