基于遗传禁忌搜索混合算法的修理级别问题研究

贾宝惠，周 帆

(中国民航大学 航空工程学院，天津 300300)

基于遗传禁忌搜索混合算法的修理级别问题研究

贾宝惠，周 帆

(中国民航大学 航空工程学院，天津 300300)

修理级别分析(LORA)是维修决策制定的一个重要工具。由于已有的修理级别分析整数规划模型涉及大量的决策变量，用传统的优化方法很难对其进行优化求解，故提出了一种遗传禁忌搜索混合算法，以最小化维修成本为目标，对LORA问题进行求解，确定最佳修理决策组合。最后通过算例的比较分析，表明了本算法的有效性。

修理级别分析；维修成本；遗传算法；禁忌搜索

中国民航大学预研重大项目(3122014P002)

0 引言

修理级别分析(Level of Repair Analysis, LORA)用来评估综合后勤保障中系统全寿命成本的影响要素，以实现最低全寿命维修成本的系统设计。LORA是一个确定失效部件应报废还是修理，以及在修理网络中什么位置执行这些活动的过程。

现有文献中讨论了不同的多层、多级的LORA模型[1-9]，这些模型无不涉及大量的决策变量，因此，通过传统优化方法如整数规划和分支定界等很难对LORA问题进行优化求解，而遗传算法及其混合策略在求解非常耗时的大规模组合问题时显示出了极高的效力。鉴于此，本文提出一种遗传禁忌搜索混合算法，将其应用于LORA问题求解，并利用算例的比较分析，表明该算法能在可接受计算时间内求得最优解。

1 LORA问题模型的建立

1.1 航空装备维修级别和层次划分

LORA分析是以维修级别与装备修理的约定层次的划分为基础的。维修级别根据装备的范围和深度区分任务，并按维修时所处场所划分等级。航空装备维修级别分为三级，即基层级(O)、中继级(I)和基地级(D)。装备修理约定层次一般划分为外场可更换件(LRU)、车间可更换件(SRU)、车间可更换件子部件(SSRU)三个层次。对于一个给定的设计，修理级别分析师必须决定哪些部件要修理、哪些部件要报废、在修理网络中何处执行这些活动，从而确定部件进行修理或报废的位置，并以最低成本满足维修要求。1.2 建立数学模型

本文研究中，设i为所研究系统的部件,i=1,2,…，n，n为部件总数；r为修理选项，包括修理、报废、移动；e为维修级别。本文参考文献[1,3,4]所描述的模型，对LORA问题进行建模，通过最小化维修成本获得最优修理决策。

建立的数学模型如下：

(1)

其中：VCr,e,i为部件i在维修级别e上执行修理选项r的可变成本；λi为部件i全寿命周期内所需维修任务的总次数；FCr,e,i为部件i在维修级别e上执行修理选项r的固定成本；Xr,e,i为决策变量，Xr,e,i=1,表示部件i在维修级别e上选择了修理选项r，否则Xr,e,i=0。

式(1)是目标函数，对执行修理和报废活动的固定和可变成本求和，并使其最小。约束条件如下：

(2)

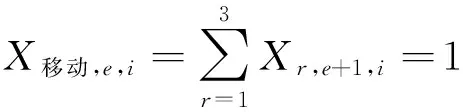
(3)

Xr,e,j=Xr,e,i,∀e,其中r=报废或者移动.

(4)

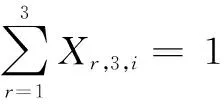
(5)

式(2)确保在基层级(e=1)选择一个修理选项。式(3)表示如果在e级上采取移动决策，在e+1级上应只采取修理决策，否则，在e+1级上不选择任何修理选项。式(4)表示子部件与父部件在各维修级别上采取相同的报废或者移动决策；j表示部件i的子部件。式(5)表示在最高级维修级别上(e=3)仅有两种修理决策(修理或报废)可供选择。

2 求解算法设计

2.1 算法思路

遗传算法和禁忌搜索(Tabu Search，TS)都是求解组合优化问题的常用算法[10]。遗传算法及其混合策略在求解非常耗时的大规模组合问题时显示出了极高的效力，缺点是当种群规模较大时求解速度较慢，而禁忌搜索又较依赖于初始解。因此，提出两者混合算法即GATS算法，克服两种算法的缺点并保留各自的优势，对NP-hard和组合优化的LORA问题进行求解。

本文的GATS算法首先生成N个初始可能解；然后利用禁忌搜索的迭代过程进行邻域搜索，对这些解进行更新；之后，流程返回遗传算法，再进行一个迭代过程；通过遗传算子产生新的后代，并根据新的后代的适应值对最佳解的禁忌表进行更新。GATS算法的终止准则是达到了预定义的连续迭代次数，迭代过程获得的最佳解相同。

GATS算法流程如图1所示。

图1 GATS算法的流程

GATS算法的具体步骤如下：

(1) 随机产生一个解集(20个解)，验证式(2)、式(3)、式(4)、式(5)。

(2) 通过邻域搜索改进解的适应度值。邻域解仅通过修改解的值为1或0获得。另外，直到验证了式(2)～式(5)，才接受邻域解。然后，更新禁忌表，其中包含所有已探索过的解的适应度值。接着，仅当适应度值不出现于禁忌表中时，探索一个新的邻域。

(3) 重复步骤(2)，直到最佳适应度值没有改进。

(4) 用最佳邻域替换该解。

(5) 基于遗传算法的选择算子和交叉算子，选择两个解来产生新的染色体。当验证了式(2)～式(5)时，接受这些新的解。

(6) 利用变异算子，生成新的染色体。

(7) 更新最佳染色体的禁忌表。

(8) 重复以上步骤，直到最佳染色体没有改进。

2.2 GATS算法设计

2.2.1 编码方式

用遗传算法求解特定问题时，首先要确定编码方式。本文采用的编码方式是一个二进制矩阵(n×d)，其中n为所有部件(即项目)的数量，d为所有修理决策的数量。该编码方式中，xij=1意味着部件i和级别j选择了修理、报废或者移动决策。图2是染色体或解的二进制编码方式，其中“项目”表示待分析产品，可以是部件或子部件。

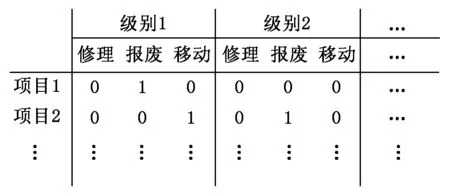
图2 染色体(修理决策)的二进制编码示例

另外，任何技术系统都可视为装配的集合，这些装配又可视为一些子装配的集合。出于建模的考虑，系统分解结构用一个矩阵来表示，称为共性矩阵，如图3所示。其中列代表父部件，行表示子部件，子部件4、5、6属于父部件3，或者说父部件3包含了子部件4、5、6。根据式(4)，无论何时父部件3采取报废或移动决策，子部件4、5、6都将采取同样的决策。

图3 系统结构的矩阵表述

2.2.2 适应度函数

本文的目标函数是求解最小值问题，算法的选择过程采用轮盘选择法，因此本文采用的适应度函数为：

F(f(x))=Cmax-f(x).

(6)

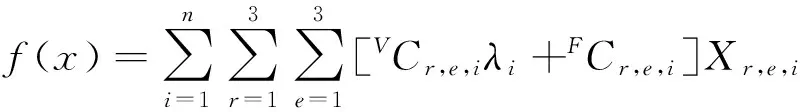
2.2.3 遗传算法算子

GATS算法使用适应度值比例选择的轮盘赌抽样作为交叉算子。每一代采用最优保存策略，用满足式(1)的最好的解替换最差的。选择一对父代进行交叉运算产生两个新的子代。交叉算子通过交换信息作用于这两个父染色体。由于每一对父代染色体的基因密码有着相同的结构，因此随机选择交叉点进行单点交叉，接着根据式(4)调整子代修理决策。

变异运算是遗传算法的另一重要特点，是产生新个体的辅助方法，变异运算的目的是维持群体的多样性，防止解陷入局部最优。本文中变异算子从最优解列表中随机选出一个染色体，并用一个同样是随机产生的新的染色体替换；另外，选择一个最优解，并随机为部件产生一个修理决策；然后再根据式(4)调整修理决策。

2.2.4 邻域结构

TS的框架由产生自初始解的一些邻域解组成，通过目标函数对这些解进行评估并分类。禁忌表通过最优解的适应度进行更新，然后确定一个新的解并从中产生额外的邻域搜索。当一系列迭代之后最佳解保持不变时，便求得了最优解。本文采用互换的方法产生邻域结构。

2.2.5 禁忌对象和禁忌表的确定

本文将禁忌对象设定为状态本身，将每次迭代最终接受的解作为禁忌对象放入禁忌表中。禁忌表是禁忌对象的集合。

3 实例分析

本节将根据数值实验的结果测试GATS算法的有效性。为了比较起见，对文献[3]执行过的案例进行研究。文献[3]中给出了航空发动机的三层结构和两级修理网络，以及所有项目在不同级别上不同修理选项的固定成本和可变成本。另外，图4给出共性矩阵，显示父部件(项目1到项目10)与子部件(项目11到项目32)之间的关系。用MATLAB语言对GATS算法进行编译，并在电脑上实施该算法。表1为本文GATS算法获得的最优解，与文献[3]的修理决策相同。另外，文献[7]中也对文献[3]执行过的案例进行了研究，其中所使用的免疫粒子群算法(IA-PSO)和本文GATS算法得出相应的总维修成本分别是4 277.27美元和4 216.27美元，计算时间分别为32 s和21 s，如表2所示。

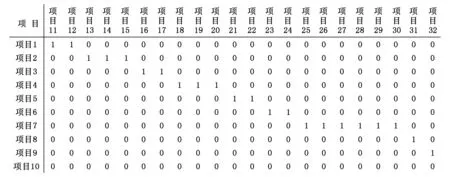
图4 共性矩阵

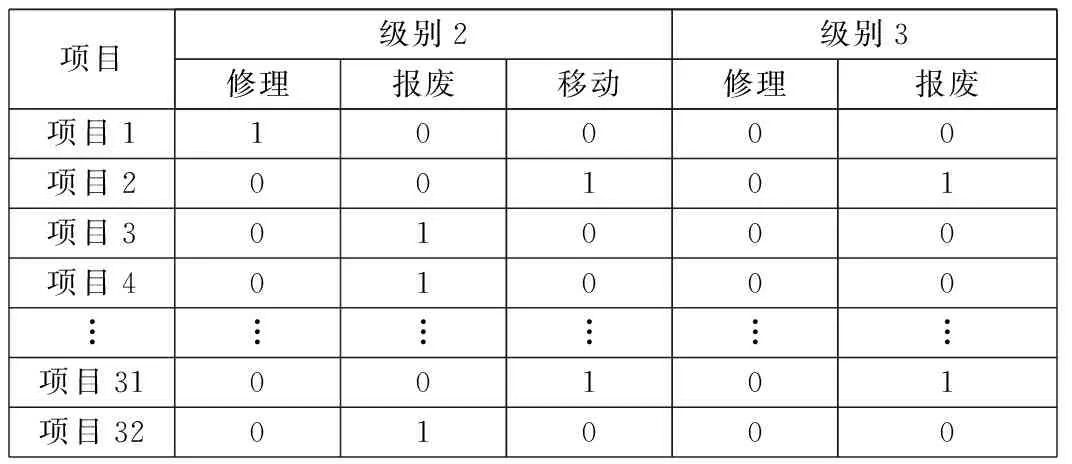
项目级别2级别3修理报废移动修理报废项目110000项目200101项目301000项目401000︙︙︙︙︙︙项目3100101项目3201000

表2 IA-PSO与GATS算法比较

4 结论

(1) 在现有LORA研究的基础上，对LORA问题进行了建模，以最小化维修成本为目标，获得最佳修理级别决策。

(2) 利用遗传-禁忌搜索混合算法，对LORA问题进行了优化求解，并给出了算法的求解步骤。利用文献[3]中的数据，通过算例的比较分析，对三级修理网络和多级系统结构的修理决策进行了优化，结果表明在合理的时间内可获得LORA问题的最优解，证明该算法是切实可行的。与免疫粒子群算法的比较结果表明了本文算法的有效性。

(3) 与相关文献研究结果相比，本文提出的算法更适于求解涉及大量决策变量的LORA问题。结合工程实际对LORA模型进行改进后，可以用本文提出的算法对LORA问题进行优化求解，为维修决策的制定提供参考。

[1] Barros L,Riley M.A combinatorial approach to level of repair analysis[J].European Journal of Operational Research,2001,129(2):242-251.

[2] Gutin G,Rafiey A,Yeo A,et al.Level of repair analysis and minimum cost homomorphisms of graphs[J].Discrete Applied Mathematics,2006,154(6):881-889.

[3] Saranga H,Dinesh Kumar U.Optimization of aircraft maintenance/support infrastructure using genetic algorithms-level of repair analysis[J].Annals of Operations Research,2006,143(1):91-106.

[4] Basten R J I,Schutten J M J,van der Heijden M C.An efficient model formulation for level of repair analysis[J].Annals of Operations Research,2009,172(1):119-142.

[5] Brick E D, Uchoa E. A facility location and installation of resources model for lever of repair analysis[J].European Journal of Operational Research,2009,192：479-486.

[6] Basten R J I,van der Heijden M C,Schutten J M J.A minimum cost flow model for level of repair analysis[J].International Journal of Production Economics,2011,133(1)：233-242.

[7] 吴昊,左洪福,孙伟.一种新的民用飞机修理级别优化模型[J].航空学报,2009(2):247-253.

[8] 薛陶,冯蕴雯,薛小锋,等.一种飞机修理级别经济性分析模型[J].航空学报,2013(1):97-103.

[9] 薛陶,冯蕴雯,代晓明.基于改进AHP方法的飞机修理级别经济性分析[J].火力与指挥控制,2013(3):58-61.

[10]王超.基于混合遗传禁忌搜索算法的多目标柔性作业车间调度问题研究[D].重庆：重庆大学,2012:31-44.

(英文摘要Study on Level of Repair Analysis Based on Hybrid Genetic-Tabu Search Algorithm

JIA Bao-hui, ZHOU Fan

(College of Aeronautical Engineering, Civil Aviation University of China, Tianjin 300300, China)

Level of repair analysis (LORA) is considered as an important tool for maintenance decision making. It is very difficult to solve the LORA integer programming model, which involves a large number of decision variables, using traditional optimization techniques. In this paper, a hybrid algorithm, combining genetic algorithm and tabu search, is presented. The LORA problem is solved based on the proposed algorithm to minimize the maintenance cost, thus determining the best repair decisions combinations. Finally, the algorithm is proved to be effective through a comparison study of numerical examples.

level of repair analysis; maintenance cost; genetic algorithm; tabu search

1672- 6413(2015)06- 0011- 03

2015- 01- 28；

2015- 09- 13

贾宝惠(1971-)，女，山西运城人，教授，硕士，研究方向为航空机电技术及维修工程。

TP391.7

A