正切数与集合的纯偶组合数＊

顾江民

（浙江广厦建设职业技术学院 信息与控制工程学院，浙江 东阳322100）

0 引言

正切数（戴煦数）是从许多组合问题中提出来的，在数论和组合数学中有着广泛的应用，一直是许多专家、学者研究的热点.文［1］介绍了Akiyama－Tanigawa算法，文［2］利用这种算法给出了Bernoulli数的一种新算法.本文利用Akiyama－Tanigawa算法给出正切数的一种新算法.笔者发现，正切数与一类数有着密切的关系，我们称之为纯偶组合数.

定义1 由

确定的系数G（n，m）称为纯偶组合数（m为正整数）.

定义2［3］正切数Dn定义为：

我们看正切数表，它的算法是：第零行数是1，1，1，…，第一行数－1·1＋3·1，－4·1＋10·1，－9·1＋21·1，…，即为2，6，12，…，第二行数－1·2＋3·6，－4·6＋10·12，－9·12＋21·20，…，即为16，96，312，…依次规律，第n行第m个数为an，m，确定第n＋（）1 行第m个数an＋1，m为：

由这种递推关系得到一个类似杨辉三角的数表，可以确定各行的首位数为正切数（图1）.运用文［2］的方法可以得到第n行的首位数为：

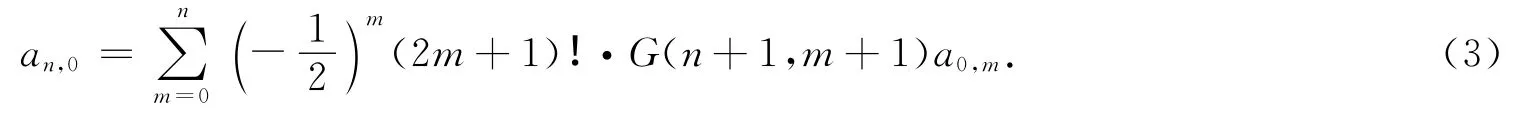
1 主要结论

定理G（n，k）为纯偶组合数，则正切数：

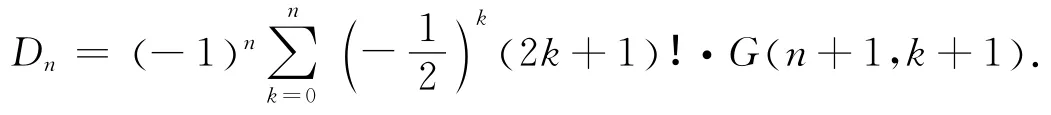
图1 正切数表Fig.1 Tangent table

推论 伯努利数：

2 纯偶组合数的性质

性质1G（n，1）＝1，∀n∈N＊；G（n，m）＝0，（n＜m）.

证明 由

易得：

故有G（1，m＋1）＝0.

性质2 纯偶组合数有以下递归关系［4～8］：

证明 设函数：

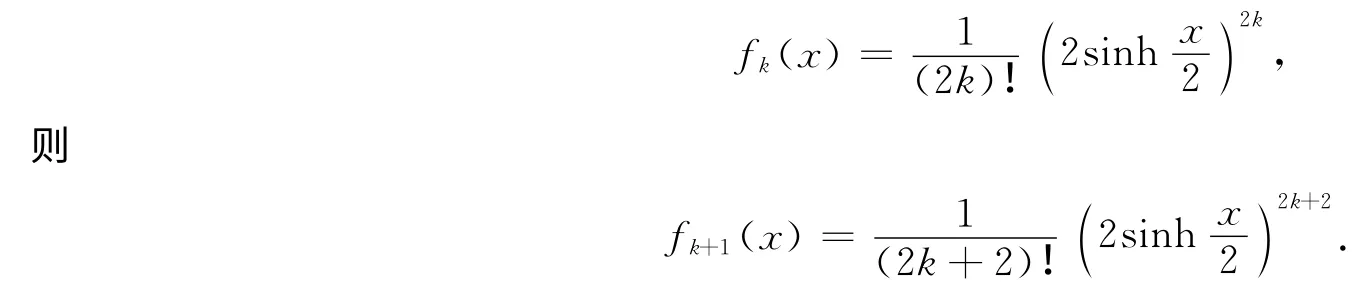
首先由（1）式可知：

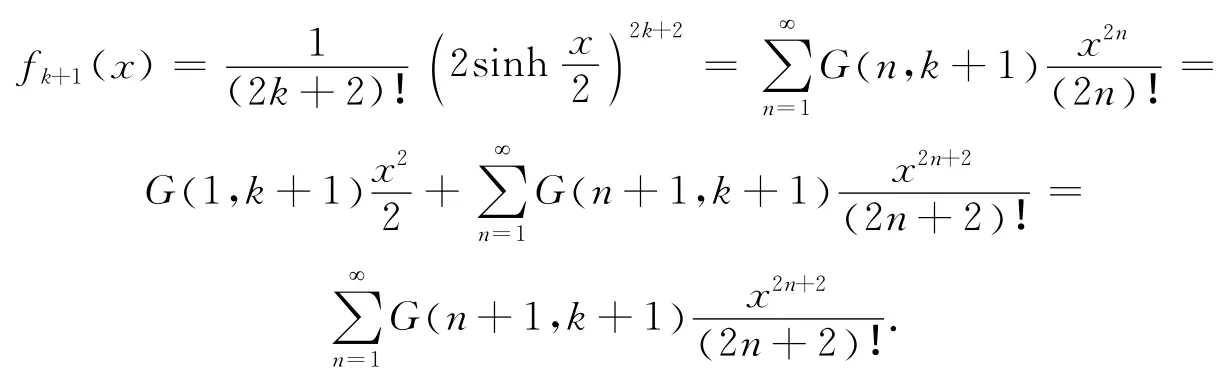
则有：

其次，因为：

对比（4）式与（5）式x2n系数可得：

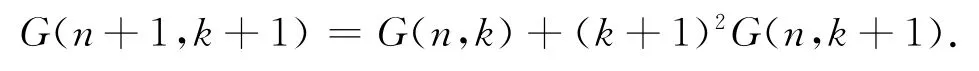
3 定理的证明

证明 设

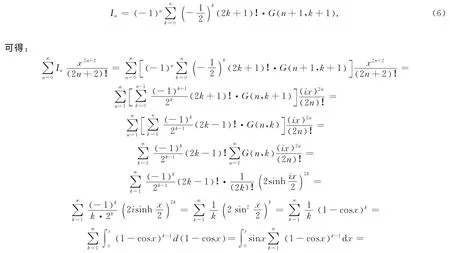
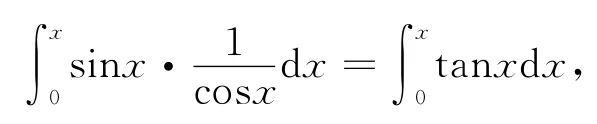
即

两边求导得：

根据定义2可知：

所以，

正切数与Bernoulli数有关系式［5］：

4 同余式与附表

利用正切数表的有关性质可给出几个同余式.

对任意的正整数n，m，k，有：

一般地，设g（n，k）组成的下三角矩阵是G（n，k）组成矩阵的逆，即

（g（n，k））＝（G（n，k））－1.

则有：

纯偶组合数阵G（n，k）见表1，纯偶组合数阵的逆g（n，k）见表2.

表1 纯偶组合数阵G（n，k）Table 1 Pure even combinations matrix

表2 纯偶组合数阵的逆g（n，k）Table 2 Pure even combinations inverse matrix

［1］Akiyama S，Tanigawa Y.Muktiple zeta values at non－positive integers［J］.The Ramanujan Journal，2001，5（4）：327－351.

［2］Kaneko M.The Akiyama－Tanigawa algorithm for Bernoulli numbers［J］.Journal of Integer Sequences，2000，12：1－6.

［3］罗见今.徐有壬《测圆密率》对正切数的研究［J］.西北大学学报（自然科学版），2006，36（5）：853－857.

［4］顾江民，朱伟义.二进纯偶多项式及应用［J］.咸阳师范学院学报，2010，25（2）：11－14.

［5］顾江民.方差多项式与Bernoulli多项式［J］.江西科学，2011，29（4）：450－452.

［6］顾江民.Euler数与集合的纯偶排列数［J］.渭南师范学院学报，2013，28（12）：5－9.

［7］朱伟义.高阶Bernoulli数与Stirling数的几个恒等式［J］.大学数学，2006（1）：83－85.

［8］王天明.近代组合学［M］.大连：大连理工大学出版社，2008.