空间计量回归分析在旅游季节性研究中的应用*
2015-12-05王彦龙
王彦龙
(安徽工商职业学院 旅游管理系,安徽 合肥231131)
0 引言
经济活动空间规划的重要性已成为共识(Clarke,1997).但在旅游经济研究中,传统计量方法的空间均质假定以及对区域之间的经济活动相互联系的忽视[1],使得经济活动中具有重要影响的地理空间效应无法被经济模型捕获,导致估计和检验上的偏误和不一致.因此,在旅游的季节性研究中应用空间效应理论是很必要的.GIS技术在地理空间活动的检测中得到应用,为区域经济分析以及决策提供比较精准的信息,也为各种区域经济活动找到适当的区位成为可能,为区域资源禀赋和区域间经济合作的理解和诊断提供了一种更为行之有效的办法(Prastacos,2000)[2].本文综合考虑旅游产业在空间维度和时间维度两方面的不平衡性,阐述空间计量分析方法在这两个维度应用的可行性,为旅游的季节性研究提供定量分析研究的新思路.
1 旅游空间的特性
1.1 旅游空间异质性
空间异质性的概念近年来在经济、管理、社会等诸多领域得到了广泛应用,其含义和用法也得到了延伸和扩展.空间异质性在经济研究领域中的应用主要集中在经济关系或经济行为在空间上存在的不稳定性,其在模型中体现为区位变化时考察变量、模型参数以及误差项方差的变动情况[3].在现实应用中主要体现属性值空间分布转台的非随机性和非均质性.具体而言,空间异质性主要包括空间单元自身在形状、大小等方面的非均质性,以及经济现象自身在空间上的非平稳结构[4].
空间异质性理论在旅游产业中的应用和表现更加广泛.旅游产业涉及空间位置、资源价值垄断、自然气候多样(日照、温度、湿度、降雨量等),以及产业结构、市场关联效应、经济发展(基础设施建设、旅游接待能力、社区居民友好程度)等诸多特点,其空间多样性显而易见,无论从地理属性还是产业属性,旅游产业都不应被描述为均匀场[5].因此,传统计量方法中固定重复抽样的Gauss-Markov假定显然不再适用,在旅游产业研究分析中纳入空间异质性是必要的[6].如在空间维度的旅游空间分布研究中使用地理加权回归GWR(Geographic Weights Regress)模型将会大大提高模型的效度和与现实情况的贴合度.
1.2 旅游空间依赖性
空间依赖的基础是地理学第一定律(Tobler First Law):“任何事物在空间上都是关联的;距离的远近程度与关联程度是呈反比状态的,距离越近则关联程度表现为越强”.空间依赖程度能够利用空间自相关(spatial autocorrelation)的统计来度量,当相邻地区属性值倾向于收敛趋势时表现为空间正自相关,当区域属性值何相异值趋向于相邻时表现为负空间相关性[7].
当旅游属性值得出的观测样本在空间分布上表现为非独立和非随机(yi=f(yj),i=1,2,…,n,i≠j)时,便可确定其具有旅游空间自相关,且该相关性可用变量间的协方差与变量方差平方根比值描述.如:某一特定位置每天的日照时间(或降雨量、风速、湿度等变量)记录,这些记录将显示出某气候属性随时间变化的规律,如多天高降雨量通常被另一个高降雨量天气跟随,低降雨量天数也可能被低降雨量天气跟随,表明存在时间维度的旅游季节性[8];当旅游收入、游客消费等指标在相邻空间单元间收敛时,则表明存在有空间维度的季节性(空间集聚)[9~12].空间统计与空间计量为空间数据的分析和研究提供了一种新的工具和方法.
1.3 空间权重矩阵
在空间计量经济学中,“经济距离”和“空间距离”是空间权重矩阵中最常用的两个权数确定标准.在旅游产业研究中,时间是游客让渡价值与旅游活动的重要约束变量,属于需优化配置的“稀缺资源”,因而“时间距离”在旅游空间计量分析中也是必须考虑的要素之一[13~16].在实际应用中,以市场价值将“时间距离”量化,纳入“经济距离”范畴.
1.3.1 空间距离
空间距离一般通过旅游吸引物之间的直线距离公式或连通渠道网络的真实交通距离测算,而线与面的距离可用距离和方向维度的均值加以代替.根据地理学第一定律(TFL),空间效应将随着空间距离的增加而衰减.在旅游空间计量应用中,“相邻距离”和“有限距离”两种赋权方式更具合理性.通常用空间权重矩阵表示对地点组合邻近度的计量,描述旅游分析中旅游流的规模、方向、旅游辐射强度或旅游经济行为的扩散速度等解释性变量的有效性[17].
空间距离的权数设定最常用的是相邻距离.视空间单元的位置进行赋值,位置相邻为1,不相邻为0.空间单元数量为n时,形成N×N阶0-1相邻矩阵W.依据相邻距离赋值权数的设定一直饱受争议.Pace(1997)提出有限距离的权数设定,设定dij为两区(不一定相邻)间的欧几里得距离,dmaxi为空间相关距离的最大值,空间单元为i,当dij≤dmaxi时,wij为1,否则为0.此时wij=0,可对有限距离的权数矩阵加以行标准化.
1.3.2 经济距离
Case等曾提出“经济距离”赋权法.“经济距离”一方面指以交通成本、时间、便利程度或舒适程度等表示两地之间的距离;另一方面也可指不同空间单元间的经济差距、旅游吸引物品质差异等概念.在旅游应用中,经济距离指旅游者在旅游客源地与目的地之间往返所需的旅行时间、交通等费用的综合或空间单元间的经济发展差距等[18].
“经济距离”赋值的影响因素主要是非负性、有意义和有限性等.在旅游收入差距研究中,两个区域的经济距离是:dij=|zi-zj|,其中zi、zj是两个区域的居民收入.当zi=zj时,wij=0,逆距离权数设定为wij=1/dij.由于经济距离涉及要素众多,包含众多定性指标且指标间具有量纲差异,导致其使用尚有诸多争议,还需进一步完善.
1.3.3 文化距离
“文化距离”在旅游空间维度和时间维度的季节性研究中都具有重要意义.文化特征是旅游吸引物的重要属性之一,也是其吸引力大小的重要衡量指标.当研究不同旅游吸引物空间单元的文化差异程度,进而评价旅游客流的季节性特征时,便可将“文化差异程度”作为解释变量纳入空间回归模型.如某空间单元文化特征突出,旅游吸引力辐射范围和强度较大,则其空间集聚效应就越强(至少在空间维度上如此)[19~21],但同时必然削弱其辐射范围内其他旅游吸引物的客流集中趋势,这样便形成了空间依赖效应.
2 空间计量模型
空间计量经济学是计量经济研究中极为重要的方向,但一直以来忽视空间效应的研究,以及模型估计中普通最小二乘法的使用,使实际经济研究的结果缺乏实践解释力.空间计量方法的出现和应用可以有效地弥补传统计量的不足.
在空间计量经济研究中主要使用的模型为空间自回归模型.空间自回归模型(SAC model)的一般形式为:
y=ρW1y+Xβ+u,
u=λW2u+ε,
ε~N(0,σ2In).
其中:X代表解释变量;y和W1为被解释变量;W2为残差项(标准化)的空间加权矩阵.
(1)当ρ=λ=0 时,表示模型中的数据不呈现空间效应,为普通回归模型.
(2)当β=λ=0,ρ≠0时,为一阶空间自回归模型,模型形式为:
y=ρW1y+ε,
ε~N(0,σ2In).
其反映的是由于邻区被解释变量的变化引起的对被解释变量的影响.
(3)当ρ≠0,λ=0,β≠0时,为空间自回归(混合回归)模型(SAR model),模型形式为:
y=ρWy+Xβ+ε,
ε~N(0,σ2In).
可以看出,被解释变量受本区域解释变量和邻近区域被解释变量的双重影响.
(4)当ρ=0,β≠0,λ≠0 时,为残差空间自回归模型(SEM model),模型形式为:
y=Xβ+u,
u=λWu+ε,ε~N(0,σ2In).
该模型反映被解释变量受本区域解释变量X、邻区被解释变量Wy和解释变量WX的影响.
3 旅游季节性的空间计量模型
季节性是制约我国旅游业发展的重要原因之一.对旅游季节性的准确理解是实现反季旅游“资源”开发的前提.旅游季节性的本质是反映旅游市场的不平衡性,而这种不平衡性可从两个维度加以理解:一是时间维度的季节性,即狭义的旅游季节性;二是空间维度的季节性,可从旅游资源禀赋、劳动力、资本、技术以及旅游生理属性等多个方面的空间不平衡性加以考虑,从旅游产业角度确定区域发展的环境约束等(Kalinsk,1999).见图1.

图1 旅游季节性的二个维度Fig.1 Two dimension of tourism seasonality
3.1 时间维度的旅游季节性
从时间维度来说,导致旅游季节性的不平衡因素很多,主要有自然气候条件(日照、温度、湿度、风速、降雨量等)、节假日制度和宗教文化习俗等.旅游季节性研究可以分为旅游季节性在统计学上的显著性检验和当某景区或旅游目的地区域具有显著的旅游季节性时进行计量回归分析.
假设某海滨景区在一年中每天的游客数量或收入记录,相关图示可能会显示游客数量或收入在时间维度上一定的变化规律.我们可将一年的数据分为12个月,便能获得12个时间段的数据,在每个时间段(每个月)有时间序列{Xt,1},{Xt,2},{Xt,3}…按照序列相关系数计算方法,首先计算获得各数据序列的均值.
例:

然后根据公式计算序列相关系数:

当n值较大时,1/(n-1)与1/n非常接近,两个序列数据的均值与标准差的差异可忽略不计.公式可进一步化简为:

该式为延迟一个时段的序列相关系数.延迟k个时段的序列相关系数可用类似公式:

在确定各时间序列具有显著相关性后,可构建如下计量回归模型:
响应变量Yi为旅游季节性程度指标,表示为淡季与旺季的数据差异,如旅游消费旺季峰值与淡季谷值差异.Yi由解释变量Xij(自然气候条件、经济发展水平、空间地理属性、旅游吸引物属性……)和随机扰动项ui决定,进一步确定计量分析模型:

引入相关数据后就可估计出相关解释变量对旅游季节性产生的贡献度.
3.2 空间维度的旅游季节性效应(空间集聚效应)
空间维度集聚效应①为了和狭义旅游季节性概念相区别,下文中使用空间集聚效应表示空间维度的旅游季节性.产生的原因主要有经济发展水平(基础设施建设、旅游接待能力、社区居民友好程度……)、旅游资源禀赋(吸引物价值垄断(自然风光、宗教、民族文化等))、地理空间属性(空间自相关、厚市场效应(thick markets))以及外部性等.
Anselin(1988)提出混合空间自回归模型:

其中:y是n×1阶因变量向量;W是空间权重矩阵;X是n×k阶的解释变量矩阵,一般是一阶相邻矩阵;ρ为空间滞后变量对被解释变量的影响.在实际应用中,该模型还在标准回归模型中考虑了空间滞后因变量.Anselin(1988)同时给出了求解过程:
首先对y=Xβ0+ε0执行OLS回归,再对Wy=XβL+εL执行OLS回归,计算剩余误差:
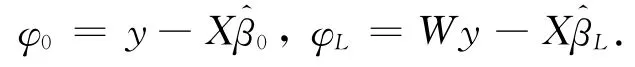
最后利用φ0和φL给出似然函数:

求得使函数最大值的ρ.利用求出的ρ计算:

用单变量优化算法寻找基于自然对数似然函数的最大似然估计,并用Hessian矩阵方法估计参数离散度.GWR 模型则扩展了传统的全局回归模型,允许空间上的局部参数估计:

模型中,(μi,νi)是指第i个空间样本单元坐标.在全局回归模型中,βk(μi,νi)将不会随着空间样本单元i的变化而变化,即取恒定值:βk(μ,ν).而在GWR 模型中,βk(μi,νi)将随着空间样本单元位置即坐标(μi,νi)的改变而不同.可以得出,GWR 模型是空间变系数回归模型的一种.依据与位置i越接近的观测数据将对估计产生更大的影响思想(Fotheringham、Brunsdon和Charkton1996),利用加权最小二乘进行估计:

其中:W是空间权重矩阵.
3.3 广义空间计量回归模型(SAC,Spatial Autocorrelation Model)
Anselin提出了SAR和SEC模型的选择判别准则:当MoranI检验为显著时,对最大似然LM-Lag比LM-Error更显著,且稳健估计R-LMLAG为显著,R-LMERR为不显著.这样就选用空间滞后模型(SAR);反之,则选用空间误差构成(SEC)模型.但由于旅游经济涉及要素广泛,表现出的季节性影响因素相互交织,从经济理论和经验常识判断,空间滞后模型和空间误差模型都无法单独完整地描述旅游季节性影响因素.按目前的技术处理能力要将空间异质性与空间依赖效应分开是有困难的,为了综合考虑旅游季节性的产生因素,需要引入广义空间模型(SAC).该模型同时包括空间滞后结构和空间误差结构,如方程组(5)所示:

模型(5)中的W1和W2可以相等.
3.4 空间过滤模型
旅游季节性研究中非常重要的一个方面是对地理空间效应的研究.无论从气候带、自然资源禀赋看,还是从经济文化发展水平看,中国区域差异是显著的.目前,横截面回归模型和面板数据模型是应用较广泛的两种模型.横截面模型只是对其在某一时点上的静态分析,不同年份的横截面样本可能产生不同的回归结果,且该模型没有考虑不同区域经济结构和社会文化以及技术的差异,难以得出无偏且一致的结论.
实际上,旅游产业发展过程中,时间维度的依赖和空间自相关都是客观存在的,其变化也是客观存在的,表现出动态演化特征.综合考虑这两种效应思路是非常清晰的:一种是设计能整合两维度效应的模型,但目前还没有可行的估计和检验方法;另一种是在估计和检验之前将输入变量中的空间效应剔除,再使用常规计量方法进行估计和检验,即我们所说的空间过滤动态面板数据模型.
Getis(2002)和Griffith(2003),Getis和Ying(2004)给出了空间过滤面板数据模型估计的如下步骤:
首先,根据Gi的定义可以获得经过空间滤值后的观测值:

接着,对空间滤值后的面板数据模型进行估计和检验.
最后,对估计结果进行经济地理和统计上的双重检验(如R、F、残差Moran检验等).
很多学者认为,时间序列和空间过滤的一阶差分都属于一种空间差分.但一阶差分将使行标准化矩阵奇异化是行不通的.一阶空间差分广义的形式为:

或

行标准化矩阵W的行元素之和为1,可以得出(I-W)表现为奇异(singular).假设在差分时引入空间自回归参数则变为:

(I-ρW)为空间滤子(spatial filter).(9)式两边乘以(1-ρW)-1得:

(10)式等同于空间自回归误差序列(Spatial Autoregressive Error Term)模型.用辅助回归估计空间过滤模型(10)是不可以的,只有与其他模型参数结合使用才行.
3.5 旅游季节性空间计量模型的估计与检验
20世纪60年代至80年代,对模型估计的研究是空间计量经济学的研究焦点.Besag等很多学者都研究了各种空间自回归模型的估计问题,在空间自回归模型中使用最小二乘估计不是空间计量经济模型研究的最佳选择.
80年代后,Cliff-Ord(1981)、Anselin、Haining和Anselin,以及Bera提出了最大似然估计(ML)方法,并迅速得到广泛应用.
Anselin在空间自回归模型中给出了用极大似然估计方法进行参数估计的步骤.首先需要构造最大似然函数:

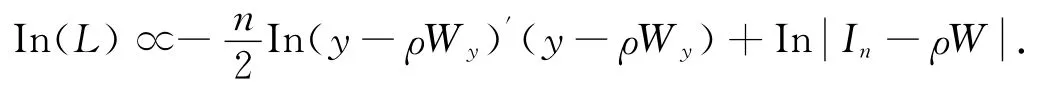
当数据量较大时,可用最大似然估计的ρ和σ2计算Hessian矩阵或稀疏矩阵函数计算似然值.近年来,Kelejian、Anselin和Prucha等人的广义矩估计(GMM)和工具变量法(IV)得到了理论界的普遍认可.
对于空间计量模型自相关性的检验,Moran最早提出了MoranI检验:

该检验是目前使用最广泛的的检验,因为其只要OLS估计或非线形优化.首先检验MoranI的空间自相关性,如果空间自相关则可建立空间计量经济模型,进一步做实证分析.此外,Geary′C比率(Geary,1954)的使用也较多.度量空间单元自相关的全局指标:

GR 为1表示随机性的空间单元地理分布模式.当GR 显著,且GR∈(0,1)时,表现为空间自相关,存在空间集聚倾向;当GR 显著,但GR∈(1,2)时,则存在负空间自相关,表示异质性空间单元具有集中倾向.
4 结论
通过对空间计量理论和方法的梳理以及相关文献综述可以看出,空间计量方法对于旅游产业不平衡性的研究具有极其重要的作用,尤其是空间计量方法的实证应用在我国的研究有着极为广阔的前景.在传统计量研究中,空间均质、生产要素可无成本和无时滞流动、空间结构在不同时间节点保持不变等假定明显脱离现实,很难保证实证的准确性.实际上,由于景区先天禀赋、自然气候和经济发展水平等要素在空间上的明显非均质性,以及要素在不同空间之间的运输成本与流动阻力问题,使得空间效应成为旅游经济发展中不可忽视的重要因素.
将空间计量模型和传统时间序列分析相结合,从时间和空间两个维度来深入分析旅游发展非均衡问题及其动态演化路径,是空间计量方法在旅游应用中的一个非常有益的扩展.今后,将时空与研究经济问题结合是经济研究的重要发展方向.运用空间思维这一新的视角,将空间计量分析作为实证工具应用于旅游产业季节性研究,将为旅游学科寻求到新的经验证据,促进旅游应用经济学科快速发展.
[1]Lesage J P.A spatial econometric examination of China,seconomic growth[J].Geographic Inform Action Sciences,1999(5):143-153.
[2]Coughlin C C,Segev E.Foreign direct investment in China:a spatial econometric study[J].World Economy,2000(23):1-23.
[3]Anselin L.Spatial econometrics:method and models[M].The Netherlands:Kluwer Academic Publishers,Dordrecht,1988.
[4]Paelinck J.Spatial development planning:a dynamic convex programming approach[J].European Journal of Operational Research,1979(3):501-504.
[5]Akerlof G A.Social distance and socialdecisions[J].Econometrica,1997(65):1005-1027.
[6]Durlauf S N.Spillovers,stratification and inequality[J].European Economic Review,1997(38):836-840.
[7]Aoki M.New approaches to macroeconomic modelling[M].Cambridge:Cambridge University Press,1996.
[8]Durlauf S N,Maccini L J.Measuring noise in inventory models[J].Journal of Monetary Economics,1995(36):65-79.
[9]Fujita M,Krugmam P,Venables A.The spatial economy:cities,regions and international trade[M].Cambridge:MIT Press,1999.
[10]Bruecckner J K.Strategic interaction among governments:an overview of empirical studies[J].International Regional Science Review,2002(44):438-467.
[11]Anselin L.Spatial dependence in linear regression models with an introduction to spatial econometrics[A].New York:Marcel Dekker,Inc,1998.
[12]Pace R K,Barry R.Sparse spatial autoregressions[J].Statistics&Probability Letters,1997(33):291-297.
[13]Cliff A,Ord K.Spatial processes:models and applications[M].London:Pion,1981.
[14]Case A,Rosen H S,Hines J R.Budget spillovers and fiscal policy interdependence:evidence from the States[J].Journal of Public Econom ics,1993(52):285-307.
[15]Anselin L.Under the hood:Issues in the specification and interp retation of spatial regression models[J].Agricultural Economics,2002(27):247-267.
[16]Fudenberg D,Tirole J.Game theory[M].Translated by HuangTao.Beijing:China Renmin University Press,2002(3):76-128.
[17]陈斐.区域空间经济关联模式分析[M].北京:中国社会科学出版社,2008.
[18]沈体雁,冯等田,孙铁山.空间计量经济学[M].北京:北京大学出版社,2011.
[19]de Smith M J,Goodchild M F.地理空间分析——原理、技术与软件工具(second edition)[M].杜培军,张海荣,冷海龙,译.北京:电子工业出版社,2009.
[20]Laffont J J.Enforcement,regulation and development[J].Journal of African Economics,2003(12):193-211.
[21]Ward M D.空间回归模型[M].宋曦,译.上海:格致出版社,2013.
