基于问题解决的数学思考──以一道课本例题为例
2015-12-05李玉荣金陵中学河西分校江苏南京210019
●李玉荣(金陵中学河西分校江苏南京210019)
基于问题解决的数学思考──以一道课本例题为例
●李玉荣(金陵中学河西分校江苏南京210019)
1 问题提出
题目点A,B分别是2条平行线上任意2个点,在直线上找一点C,使BC=AB,联结AC,在直线AC上任取一点E,作∠BEF=∠ABC,EF交直线m于点F.
1)如图1,当k=1时,探究线段EF与EB的关系,并加以证明.
说明①如果你经过反复探索没有解决问题,请写出探索过程(要求至少3步);②在完成①之后,可以自己添加条件(添加的条件限定为∠ABC为特殊角),在图2中补全图形,完成证明(选择添加条件比原题少得3分).
2)如图3,若∠ABC=90°,k≠1,探究线段EF与EB的关系,并说明理由.
(2008年辽宁省大连市数学中考试题)
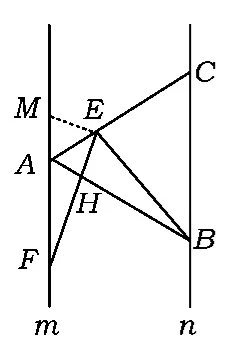
图1

图2
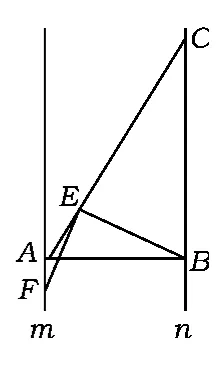
图3
笔者近期在讲授完“全等三角形”后,将第1)小题选作单元检测的压轴题,结果2个班88名学生无人能解,其他班级的情况也大致相仿,这不禁引发了笔者的思考,此题很难吗?难在哪里?
2 原解呈现
文献[1]给出的证法如下:
如图1,以E为圆心、EA为半径画弧交直线m于点M.联结EM,则

从这个证法看,本题的难点是:1)条件“∠BEF=∠ABC”的有效使用;2)构造一个三角形使EF与BE分别在2个全等三角形中,辅助线的添加无疑起到了决定性的作用.除了文献[1]中提供的辅助线“以E为圆心、EA为半径画弧交直线m于点M”(着实不易想到),能另辟蹊径破解此题吗?
3 例题引路
例1如图4,已知△ABC的角平分线AD,BE相交于点P,求证:点P在∠ACB的角平分线上.
(苏科版八年级数学(下册)第55页例2)
证明过点P作PF⊥AB,PM⊥BC,PN⊥AC,垂足分别为F,M,N.因为AD平分∠BAC,点P在AD上,所以

故点F在∠ACB的角平分线上.
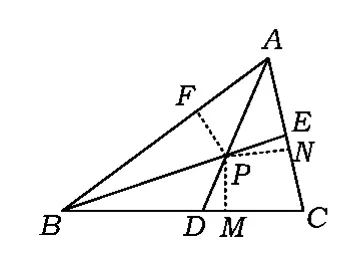
图4
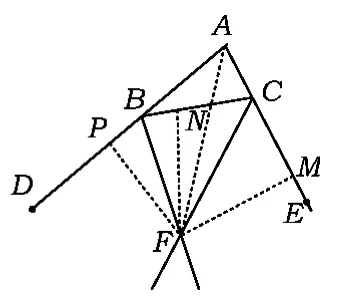
图5
例2如图5,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F,求证:点F在∠DAE的角平分线上.
(北师大版九年级数学(上册)第37页第2题)
证明过点F分别作AB,AC,BC的垂线,垂足分别为P,M,N.因为点F在∠CBD的角平分线BF上,所以
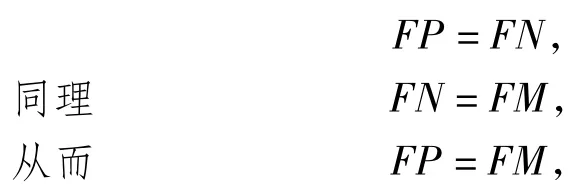
因而点F在∠DAE的角平分线上.
数学思考和问题解决是《义务教育数学课程标准(2011年版)》中提出的2个课程目标,自然应当成为数学教学的重心.而课本里的部分例题和习题,承载了编者对课程标准的把握,凝聚了编者的心血和理念,在解题思路和方法上具有典型性和代表性,在由知识转化为能力的过程中具有示范性和启发性,在编制考题时具有迁移性和再生性.这些例题的问题解决与数学思考,有助于抓问题本质,悟解题规律,练思维能力,进而在中考时触类旁通、得心应手.这2道题都是安排在学完定理“角平分线上的点到这个角的两边的距离相等”、“角的内部到角的两边的距离相等的点,在这个角的角平分线上”之后,需要证明的问题都是“某点在某角平分线上”,解决问题的关键是辅助线.由于知识点刚刚讲授,学生不难想到上面的证法,表面看来学生掌握得良好.但是,如果将问题改为证明2个角相等,学生还能自如地求解吗?在其他背景下碰到类似问题,学生还能想到这3条辅助线,通过“角相等→线段相等→角相等”解决问题吗?这正是问题解决后不容“滑过”的数学思考.
4 解法更新
证明如图6,过点E分别作EM⊥FG于点M,EN⊥AB于点N,因为m∥n,所以
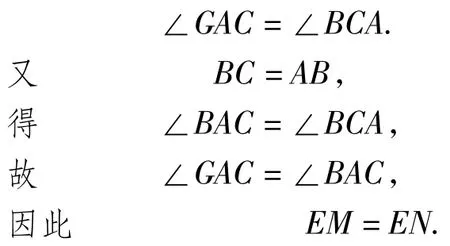

评注此证法关注了AC平分∠GAB,联想到例题的思路,辅助线的添加显得自然、合理,难点得以突破,问题也就迎刃而解了.
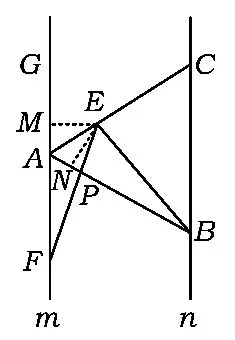
图6
5 迁移应用
例3如图7,△ABC的外角∠ACD的平分线CP与内角∠ABC的平分线BP交于点P,若∠BPC=40°,则∠CAP=______.
(2011年湖北省黄冈市数学中考试题)
分析由于题目的条件都和角有关,学生常常会直接考虑利用角的关系来求角,但思维很快受阻,无法求解.

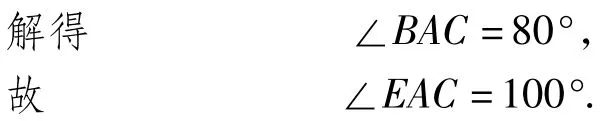
作PF⊥BD,PE⊥BA,PG⊥AC,F,E,G是垂足,由已知得
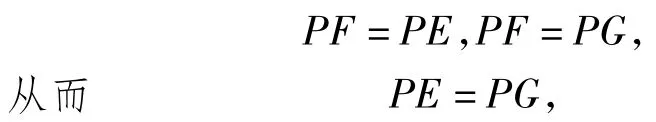
因此PA是∠EAC的角平分线,故∠CAP=50°.
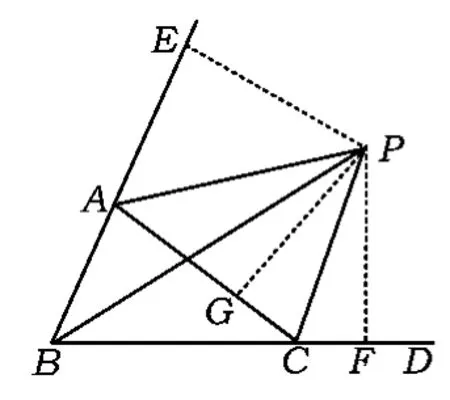
图7
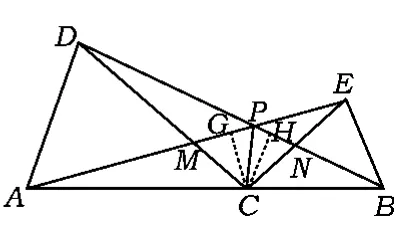
图8
评注此题是例题变式的特殊情况,由题设的角平分线联想到辅助线方能奏效.
变式1设△ABC的角平分线AD,BE相交于点P,若∠BPC=140°,则∠CAP =______.
变式2设△ABC的外角∠CBD和∠BCE的平分线相交于点P,若∠BPC=40°,则∠CAP= ______.
例4如图8,点C为线段AB上任意一点(不与点A,B重合),分别以AC,BC为一腰在AB的同侧作等腰△ACD和△BCE,CA=CD,CB=CE,∠ACD与∠BCE都是锐角,且∠ACD=∠BCE,联结AE交CD于点M,联结BD交CE于点N,AE与BD交于点P,联结CP.
1)求证:△ACE≌△DCB;
2)请你判断△ACM与△DPM的形状有何关系并说明理由;
3)求证:∠APC=∠BPC.
(2011年山东省济南市数学中考试题)
证明1),2)略.
3)过点C作CG⊥AE于点G,作CH⊥BD于点H,由△ACE≌△BCD得CG=CH,故点C在∠APB的角平分线上,即∠APC=∠BPC.
评注这是一道中考压轴题,命题者设置了2个小题作为铺垫,但要借此完成第3)小题并非易事(详见参考答案),而将问题看成证明点C在∠APB的角平分线上,只需作出相关的辅助线,问题的解决轻松自然.
变式题如图9所示,已知△ABC和△DCE均是等边三角形,点B,C,E在同一条直线上,AE与BD交于点O,AE与CD交于点G,AC与BD交于点F,联结OC,FG,则下列结论:①AE=BD;②AG=BF;③FG∥BE;④∠BOC=∠EOC,其中正确结论的个数有()
A.1个 B.2个 C.3个 D.4个
(2010年黑龙江省绥化市数学中考试题)
图9
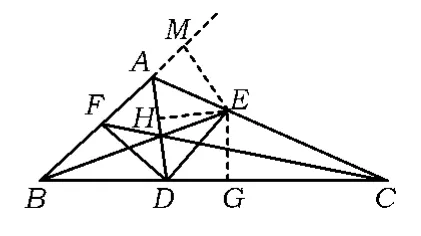
图10
例5如图10,设AD,BE,CF是△ABC的角平分线,且∠BAC=120°,联结DE,DF,求证:DE⊥DF.
(2009年“希望杯”初中数学竞赛试题)
证明作EG⊥BC,EH⊥AD,EM⊥BA,垂足分别为G,H,M.因为∠BAC=120°且AD是△ABC的角平分线,所以
又BE是△ABC的角平分线,得

于是DE平分∠ADC.同理可得DF平分∠ADB,即
进而DE⊥DF.
评注此题看似简单,入手求解顿感不易,文献[2]和文献[3]中给出了多种解法均复杂冗长,且需要用到初中生没学到的几何知识,而联想到角平分线的相关辅助线解题十分简捷.
变式题在等腰△ABC中,AB=AC=8,∠BAC=120°,P为BC的中点,小慧拿着含30°角的透明三角板,使30°角的顶点落在点P,三角板绕点P旋转.
1)如图11,当三角板的2条边分别交AB,AC于点E,F时,求证:△BPE∽△CFP.
2)操作:将三角板绕点P旋转到图12所示的情形时,三角板的2条边分别交BA的延长线及边AC于点E,F.
①探究1:△BPE与△CFP还相似吗(只需写出结论)?
②探究2:联结EF,△BPE与△PFE是否相似?请说明理由;
③设EF=m,△EPF的面积为S,试用m的代数式表示S.
(2005年江苏省扬州市数学中考试题)
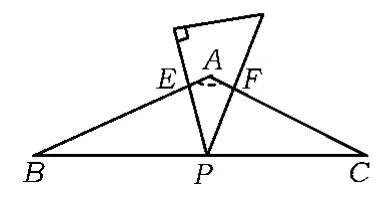
图11
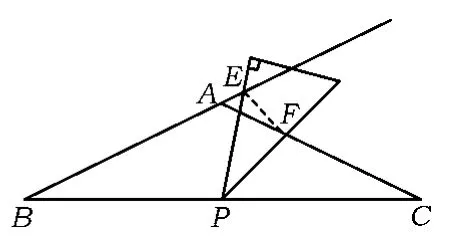
图12
例4如图13,已知AD是△ABC的中线,∠ABC=30°,∠ADC=45°,则∠ACB =______.
(2011年北京市初二数学竞赛试题)
解过点D作FD⊥BC交AB于点E,联结CE,则

即AE平分∠FEC.又∠EDA=∠ADC=45°,从而AD平分∠FDC,分别作AH⊥CE于点H,AM⊥DF于点M,AN⊥DG于点N,则
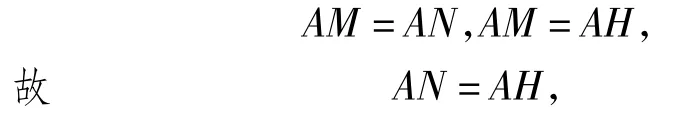
于是AC平分∠ECG,即
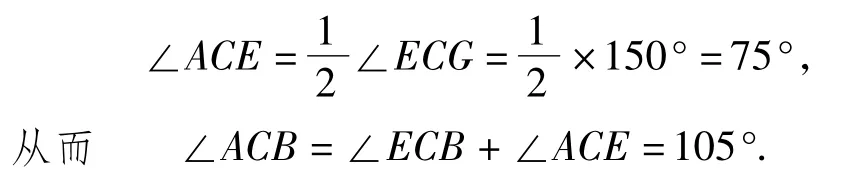
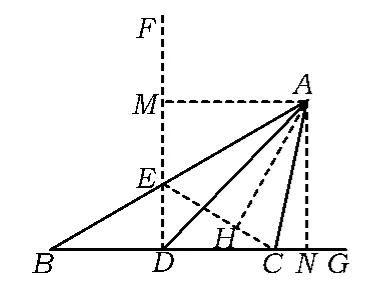
图13
图14
评注此题看似常规,实际很难入手,文献[4]提供的解法十分繁琐,恰当的辅助线构造出角平分线及其相关的辅助线使问题迎刃而解.
变式题如图14,在▱ABCD中,点E,F分别在CD,AD上,且AE=CF,AE与CF交于点P.求证:BP平分∠APC.
6 写在最后
数学新授课通常都会配置与当堂知识密切相关的例题,这些例题的解决,大多数学生并不存在困难,甚至通过自主学习就能弄懂,但后期结果常常是一看就会、一听就懂、一过即忘,究其原因是学生没有透彻地理解解决问题的方法,更缺少对问题解决的数学思考.为什么要这样做?怎么想到这样做的?你能在别的什么题目中利用这个结果或这种方法吗?还有没有更好的方法解决问题?“数学思考”是问题解决的前提,解决问题离不开数学思考,数学思考同时又是问题解决的持续,“数学思考→问题解决→数学思考”应是一个完整的链条.但在日常教学中,问题解决后的数学思考却常常被忽视,使得学生的解题能力大多停滞在模仿阶段,缺少质的飞跃,更谈不上创新思维,教学的有效性大打折扣.数学思考是指运用“数学方式的理性思维”进行的思考,它培养学生以数学的眼光看世界,从数学角度去分析问题的素养,会使学生终身受益.无论他们将来从事什么职业,学会独立思考,体会数学的基本思想和思维方式,让学生学会思考,特别是独立思考,是数学课程培养学生创新能力的核心;“问题解决”与“解决问题”并不完全相同,它不但是一种教学方式,是展开课堂内容的一种有效形式,也是学生应该掌握的学习形式和应该具备的能力.课程目标,它包括从数学角度发现、提出、分析和解决问题4个方面.实现“问题解决”的课程目标,能够让学生学会数学思考,还能够让学生积累思维经验,并且能够成为培养学生应用意识和实践能力的重要方面.在“数学思考→问题解决→数学思考”中,教师精心用好教材例题至关重要,根据学生的不同特点,采用多元化的形式,精心设计例题的教学,打造生本课堂、高效课堂,学生将能够积累数学活动经验,感悟数学思想,提高发现、提出、分析和解决问题的能力.
[1]李朝东.中考名题精讲精练(数学)[M].北京:中国少年儿童出版社,2008.
[2]刘运宜.再谈平面几何代数化背景探源[J].中学数学杂志:初中版,2009(6):44-46.
[3]姜官扬,刘小辉.两道几何题的另证[J].中学数学:初中版,2011(2):60-61.
[4]姜照华.一道平几赛题的另解与推广[J].数理天地:初中版,2012(6):29-31.
