例说高考数学试题中的“陷阱”
2015-12-05何昌俊七台河市高级中学黑龙江七台河154600何卓延世大学韩国
●何昌俊(七台河市高级中学黑龙江七台河154600)●何卓(延世大学韩国)
例说高考数学试题中的“陷阱”
●何昌俊(七台河市高级中学黑龙江七台河154600)●何卓(延世大学韩国)
高考试题源于教材,活于教材.源于教材就是尊重教材,基于教材双基,植入灵活性.尤其在灵活性上,命题者别具匠心,可谓用心良苦,设计出具有很好选拔功能的优秀试题来,值得教师学习研究.为更好落实到高三辅导教学中,笔者从应用灵活性中的一个侧面举例说明试题中“陷阱”.
1 概念“陷阱”

(2011年重庆市数学高考理科试题第7题)
解由a>0,b>0,a+b=2,得

故选C.
2 解法“陷阱”
1)求a,b的值;
(2011年全国数学高考新课标卷理科试题)
分析第2)小题较难,学生通常用分离参数法来解.学生一看此压轴题是常见的求参变量范围的问题,直接采用分离变量,然后不等式右端构造函数求最值,掉进了解法“陷阱”.破解需学生有扎实的基础知识和灵活解题的能力.
3 原型“陷阱”
例3已知数列{an}满足a1=1,an+1=3an+1.
(2014年全国数学高考新课标卷理科试题)

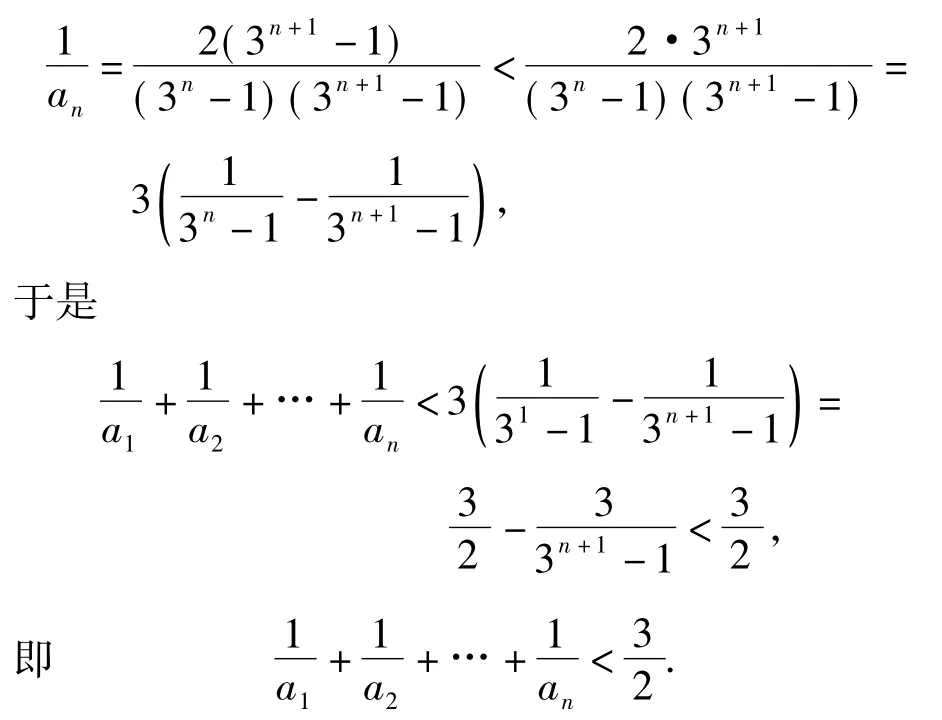
4 相似“陷阱”
例4已知正数a,b,c满足5c-3a≤b≤4c-a,clnb≥a+clnc,则的取值范围是______.
(2012年江苏省数学高考试题第14题)
分析设计貌似线性规划的“陷阱”,前一个不等式可以画出可行域,但后一个较难.灵活运用所学知识,可得如下解法:
解由clnb≥a+clnc得
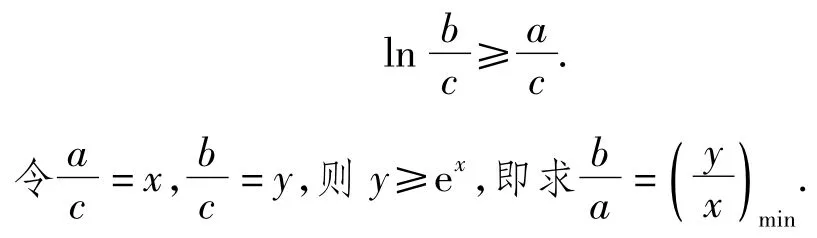
当直线l:y=kx与y=ex相切时,切点为(x0,ex0),从而y'|x=x0=ex0,于是l:y-ex0=ex0(x-x0)过点(0,0),有
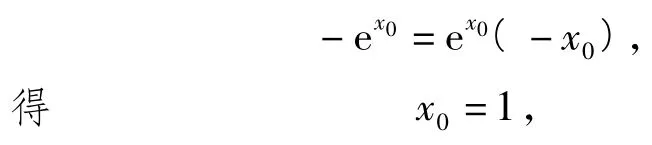
5 定势“陷阱”
例5设函数f(x)=ln(1+x),g(x)= xf'(x),x≥0,其中f'(x)是f(x)的导函数.
1)g1(x)=g(x),gn+1(x)=g(gn(x)),n∈N+,求gn(x)的表达式;
2)若f(x)≥ag(x)恒成立,求实数a的取值范围;
3)设n∈N+,比较g(1)+g(2)+…+g(n)与n-f(n)的大小,并加以证明.
(2014年陕西省数学高考理科试题第21题)
2)(-∞,1].
3)由题设得

通常采用作差法比较大小,这就是求和思维定势“陷阱”.
不要受思维定势影响,冲出固定模式,灵活运用知识可得:
解比较结果为
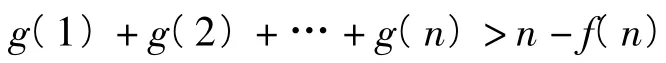
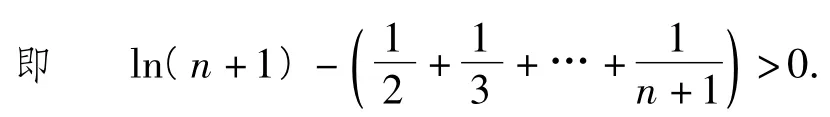
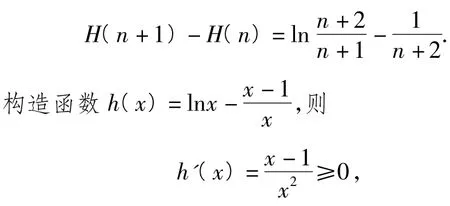
当且仅当x=1时等号成立.h(x)在[1,+∞)上单调递增,且h(1)=0.令,得
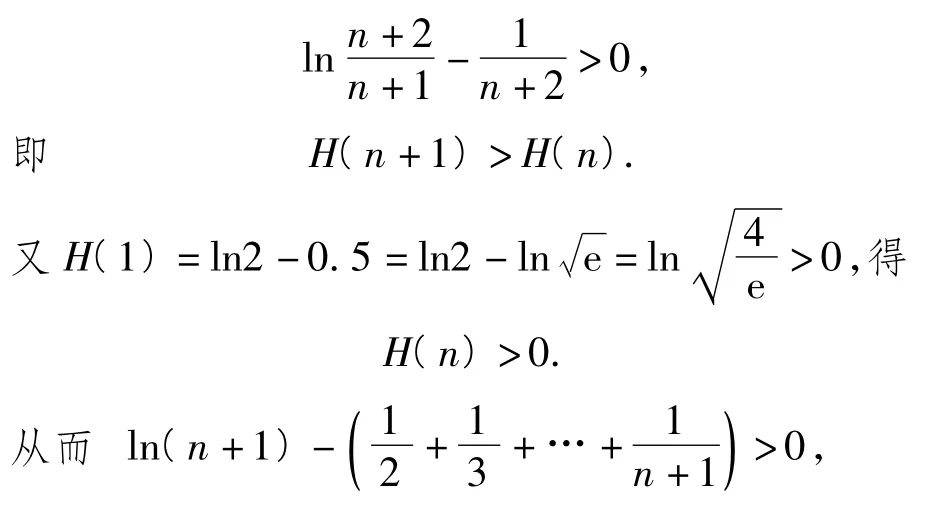
对于n∈N+成立,即
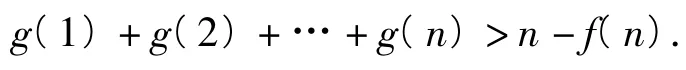
6 变式“陷阱”
(2012年全国数学高考新课标卷文科试题)
分析该题是求最值常见的题型,但函数式比较复杂,学生不知所措.实际上,设奇偶函数(变式“陷阱”)一个局,让考生破解.基础扎实运用灵活,寻找奇偶原型,即设函数,G(x)为奇函数,从而G(x)的最大值与最小值的和为0.又f(x)=G(x)+1,于是函数f(x)的最大值M与最小值m的和为2.
[1]何昌俊,姜兴东,何卓.解题教学心得[J].中小学数学:高中,2011(11):37.
