一道不等式问题的错解引发的思考
2015-12-05王荣鑫邗江中学江苏邗江225009
●王荣鑫(邗江中学江苏邗江225009)
一道不等式问题的错解引发的思考
●王荣鑫(邗江中学江苏邗江225009)
1 问题缘起
进入高三复习阶段,学生在知识体系趋于完善的同时也具备了一些基本的解题策略.但有时仍会顺题而解,落入命题的陷阱,得到错误的思路,或者选择了易想而难算的方法,与正确结果渐行渐远甚至背道而驰.罗增儒教授说过:“解题愚蠢是与解题智慧相对照的一个词,并且主要用于自己.解法不够本质、付出的解题力量大于标准解法的解题力量,都包含着解题愚蠢.”笔者一直在思考,如何才能让学生告别这些“解题愚蠢”?下面以一道不等式问题为例,结合课堂教学片断,谈一些个人不成熟的思考.
例1关于x的不等式x2-ax+2a<0的解集为A,若集合A中恰有2个整数,则实数a的取值范围是______.
(江苏省连云港市2013届高三期末考试试题)
本题是填空压轴题,考查含参不等式问题,综合性强,难度较大.
2 教学片断
2.1 错解分析
教师出示例题,学生作答.由于一元二次不等式是常见题型,学生下手很快,但大多数学生并没有得到正确结果,有些苦苦思索无从下笔,有些则迷失方向,盲目地在复杂的计算中彷徨.巡视中发现了一类错解,是笔者在备课前没有预料到的,是否仍然按照课前的预设进行讲解,短暂的犹豫之后,笔者决定先让学生谈谈自己的想法.
师:大部分同学都有了自己的想法,这道题短小精悍,貌似很“善良”,可是下手容易,得手难啊(学生纷纷点头表示赞同).现在请生1谈谈自己的想法.
生1(实物投影展示):不等式解集非空,则Δ> 0,得a>8或a<0,解不等式得:(记为x1<x<x2).因为解集A中恰有2个整数,2个整数之间的“距离”最小是1,恰好有2个就不会超过2,所以1<|x1-x2|<2,然后代入解不等式.
师:很好,生1直接解出原不等式,然后“翻译”转化题中条件“若集合A中恰有2个整数”,据此构造相关不等式,目标明确,思路清晰.对他的想法,有不同意见吗?
生2:“1<|x1-x2|<2”不是“集合A中恰有2个整数”的充要条件,画出数轴就可以举出反例了(如图1所示).
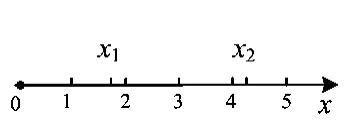
图1
师:很好,爱因斯坦说过发现问题比解决问题更重要,生2发现了生1解法中的问题,并举反例说明生1解法的错误,同时,举反例也是一种非常重要的数学能力.但我认为生1的想法中依然存在着闪光点,是否能够修正原本错误的解法?或者你有其他更优的思路吗?
2.2 错解修正
生3:我认为生1的方法很好,他已经直接解出了不等式,将关于x的一元二次不等式转化降为一次,我感觉到他已经很接近真相了.问题的关键在于题目中的“解集A中恰有2个整数”这个条件还可以怎么用?
师:你的评价很到位,那就请按照你的想法,继续下去.
生3:我认为可以考虑缩小x1,x2的范围.
(兴奋地冲上讲台投影展示)当a>8时,x=4必然是不等式的1个整数解,x2是以a为自变量的函数,在(8,+∞)上单调递增,故x2∈(4,+∞),从而
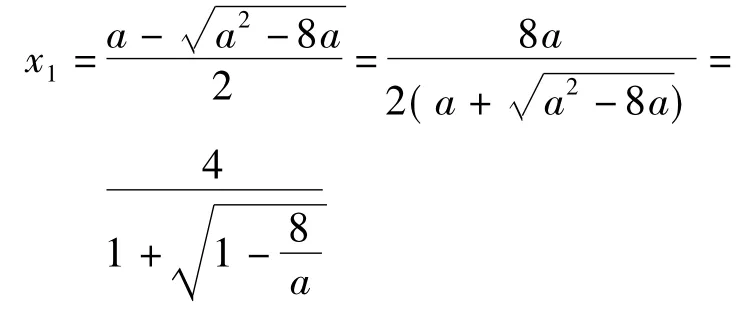
1)x1∈[3,4),x2∈(5,6],2个整数解为4和5,即

2)x1∈(2,3),x2∈(4,5],2个整数解为3和4,a∈φ.
2.3 解法优化
师:非常好,生3在前2位同学的基础上对错解进行了修正.他采用函数单调性结合估算的方法来缩小整数解可能值的范围.刚才这几位同学告诉我们,错误并不可怕,我们可以从错误的解法中探寻到正确甚至更加高妙的思路.大家对他的解法有什么评价?解法可以再优化吗?
优化1数形结合
生4:生3的的方法很好,他把x1,x2看成以a为自变量的函数,这种想法很有意思,但计算太繁了.我认为他运算基本功非常扎实,可总觉得有点“杀鸡焉用屠龙刀”的感觉(学生大笑).我想用二次函数构造函数f(x)=x2-ax+2a的图像来解决问题,但是画图好像很麻烦,进行不下去(其他同学表示有同感).
师:考虑到“三个二次”之间的联系,用二次函数解决一元二次不等式问题,是一个很自然的想法.这个函数图像的形状和位置由字母a控制,我们不妨取一些特殊值来得到特殊的图像,然后让a变化,函数图像就会“动”起来,也许能最终解决问题.下面继续尝试,看看是否能完善这种解法.
生5(投影):构造函数f(x)=x2-ax+2a,如图2,当a=8时,图像与x轴相切于点(4,0),a变大,图像向右向下移动,x1减小,x2增大,当a=9时,抛物线对称轴为,图像经过点(3,0),(6, 0),可知2个整数解必为4和5,则f(3)≥0, f(4)<0,f(5)<0且f(6)≥0,解得.当a<0时,同理可得.综上所述,,当直线经过点(3, 9)时,a=9,此时直线也经过点(6,36),则.当a<0时同理可得,故

图2

图3

图4
师:数形结合是解决不等式问题的一个重要思路.以上解法还可以再优化吗?
优化2左右分离
生6:含参二次函数图像的动态讨论太复杂,可以考虑把-ax+2a移到不等式右边,再画图.
(投影)原式可化为:x2<a(x-2),如图3,g(x)=a(x-2)是恒过定点(2,0)的一系列直线,研究抛物线y=x2图像在直线下方的部分.当a=8时,直线与抛物线相切,x=4必为不等式的解,当a>8时,a越大直线越“陡”,另一解可能为3或5.当直线经过点(5,25)时,
优化3参变分离
生7:我认为干脆就把a与x分离,分离以后,画图更容易,计算也更加简单.
(投影)原式可化为:x2<a(x-2),当x>2时,;当x<2时,.令x-2=t,则,研究“打勾函数”的图像在直线y=a-4下方的部分.如图4,p(1)= p(4)=5,,p(2)=4,则2个整数解为2或3,故

师:生1紧扣已知条件直接解出含参不等式,生2利用数轴举出反例,生3在前面2位同学的基础上率先得到了正确的结论,生4~生7各显神通,利用数形结合,使抽象问题具体化,让我们大开眼界.其中生7运用参变分离,避开二次函数图像的动态讨论,又进一步降低了计算量和思维的难度.不知不觉中,我们从错误走向了成功.大家在解题过程中的表现都非常棒!
3 几点思考
以上是高三一轮复习课的一个片段,一个始料未及的错误,打乱了笔者的教学方案,但也正因为此,才多了一些意外的收获和体会.通过对这道题目的讲授,笔者有如下一些思考:
3.1 成功⇒错误
在巡视学生做题时,笔者发现班上约有20%的学生都犯了与生1相同的错误,立即调整了原本的教学方案,直面这个意外的错误.但如果只是简单地指出错误,就失去了一次绝佳的“纠错”良机,因此笔者选择让学生自己去发现并纠正其中的错误.黑格尔说:“错误本身是达到真理的一个必然的环节.”在平时的教学中,教师不能轻易批评或者否定学生的错误做法,不能强行修改学生的思维轨迹,而应选择适当的教学方式,引导学生发现原有思维轨迹中的偏差,多角度剖析、探讨、反思错解,并对已有的错解作出修正和优化,消解学生“畏错”的心理障碍,让学生探索、发现错误中所蕴藏的成功契机,渐渐告别“解题愚蠢”,在“知错→议错→纠错”的过程中品味成功的喜悦.
3.2 学生≥教师
本题是一道高三期末考试的“把关题”,据命题人透露,某重点高中本题平均得分为0.2分,难度颇大.原教学方案是学生思考然后教师直接讲授,但是受生1、生2启发,笔者决定让学生自由思考发言,教学过程居然出乎意料的顺畅,学生的好点子层出不穷,真可谓惊喜连连.教师要坚信“弟子不必不如师,师不必贤于弟子”.就解题教学而言,每一种解法都是一个思维的终极结果.如果教师缺乏对学生的信任,在解题教学中忽视学生思维形成的过程,直接将解题过程扔给学生,学生就会从课堂的参与者退化成教师解题的旁观者,甚至异化为数学的厌恶者,一旦离开教师就无所适从,不会独立思考.在课堂教学中,教师虽然“闻道在先”,但也要大胆放开手,给予学生充分的信任,将课堂的主动权交还给学生.
3.3 对话⇒生成
在授课过程中,由于课堂没有完全遵照自己预设的走向,笔者内心其实是有些许忐忑的.但在与学生的对话中,认真倾听学生的想法和做法的同时,带领学生探索思考,学生顺利地得到了笔者本来准备花费巨力去讲解的“简洁”解法,笔者真切地感受到了一种酣畅淋漓的痛快.在日常教学中,教师要敢于调整自己的教学方案,引导学生在关键处对话,在质疑中释疑,让数学思维在自由对话中动态生成.教师“不能垄断课堂上的话语权,但也不能放弃课堂上的话语权”.教师要充分利用自己的“术业专攻”,引导学生在解题过程中对话,比较与评价不同的思路,引导学生思考一系列的问题.例如怎样才能得到这些思路?这个思路的错误在哪里?已有解法是否可以再优化?是否可以削减解题中冗余的思维回路?所有解法的共性是什么?一旦学生的主动性被唤醒,话语交锋引发出思维碰撞,会击穿妨碍思维的魔障,激活学生的多元思维,提升理性思维的广度和深度,生成真正属于自己的“解题智慧”.
行文至此,以罗增儒教授的一段妙语结束本文,并与诸君共勉:“即使我很笨,我也有机会通过解题过程的分析而学会聪明,并且聪明是由自己习得的.”
[1]罗增儒.解题分析——再找自己的解题愚蠢[J].中学数学教学参考:上旬,1998(4):21-22.
[2]徐明.小填空,大乾坤——一道统考题的命题构思与反思[J].中学数学教学参考:上旬,2013(6):61-63.
[3]水菊芳.我们不是课堂“神话”的缔造者——“将课堂交给学生之我见”[J].中学数学教学参考:上旬,2013(12):26-29.
[4]罗增儒.中学数学解题的理论与实践[M].南宁:广西教育出版社,2008:251.
