也谈曲线切点弦的处理方法
2015-12-05吴斌王怀明会宫中学安徽枞阳246740
●吴斌 王怀明(会宫中学安徽枞阳246740)
也谈曲线切点弦的处理方法
●吴斌 王怀明(会宫中学安徽枞阳246740)
文献[1]由一道测试题提出一个问题:过圆外一点作圆的2条切线,如何求2个切点所在直线的方程?然后通过对大纲版教材和人教A版教材处理方法的比较,得出结论:大纲版教材的处理方法(即下面的解法1,笔者注)“求解思维转弯多,且对圆的一般位置需要另行推理,这对学生而言,有一定的困难”;人教A版教材的处理方法(即下面的解法2,笔者注)“优于大纲版教材,主要表现在计算快、转化少,突出圆的地位而淡化切(直)线方程”.
事实真的是这样吗?本文先列举文献[1]中的2种解法,并增加解法3;然后通过解法的应用,比较3种解法,得到不同解法的适用范围.
1 解法呈现
为了方便说明,将文献[1]中的问题一般化:
过圆C:x2+y2=r2外一点A(x0,y0)作圆的2条切线,切点分别为P(x1,y1),Q(x2,y2),求切点弦PQ所在的直线方程.
解法1因为圆C在点P(x1,y1)处的切线垂直于OP,当x1y1≠0时,,所以圆C在点P处的切线斜率为,方程为
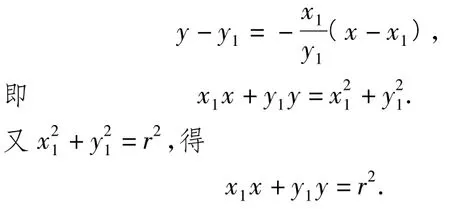
当x1=0或y1=0时,切点弦也满足方程
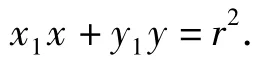
同理圆C在点Q(x2,y2)处的切线方程为
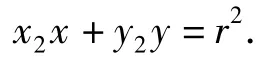
而点A(x0,y0)在切线上,有
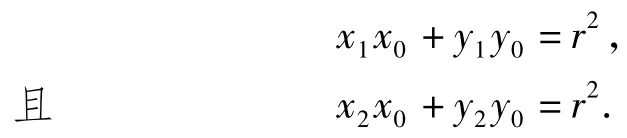
这说明点P,Q的坐标满足x0x+y0y=r2,因此切点弦PQ的方程为x0x+y0y=r2.
解法2由题意知,OP⊥AP,OQ⊥AQ,因此,点P,Q在以AO为直径的圆上.设点M(x,y)是以AO为直径的圆上任意一点,则

即以AO为直径的圆的方程为
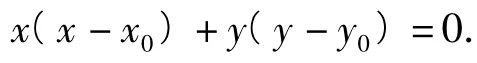
由题意知点P,Q既在圆C上,又在以AO为直径的圆上,x(x-x0)+y(y-y0)=0与x2+y2=r2相减得x0x+y0y=r2,因此切点弦PQ的方程为
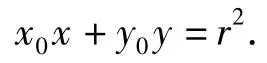
解法3当切线的斜率存在时,设切线斜率为k,则过点P(x1,y1)的切线方程为

同理可得圆C在点Q(x2,y2)处的切线方程为
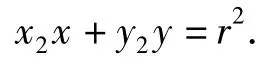
而点A(x0,y0)在切线上,得
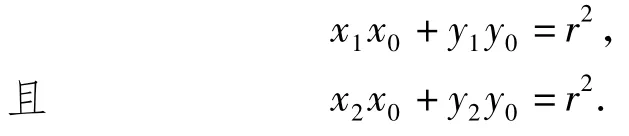
这说明点P,Q的坐标满足x0x+y0y=r2,因此直线PQ的方程为
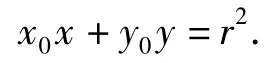
当切线的斜率不存在时,切点弦也满足方程
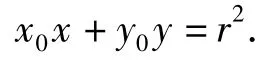
说明解法1利用性质“圆心和切点的连线垂直于过该点的切线”,直接求出切线的斜率;解法3从代数角度处理问题,利用直线和圆相切时的判别式Δ=0求出斜率,它们后面的处理方法完全一样.
2 解法的应用
例1已知抛物线C的顶点为原点,其焦点为F(0,c)(其中c>0)到直线l:x-y-2=0的距离为设P为直线l上的点,过点P作抛物线C的2条切线PA,PB,其中A,B为切点.
1)求抛物线C的方程;
2)当点P(x0,y0)为直线l上的定点时,求直线AB的方程;
3)略.
(2013年广东省数学高考试题)
解1)过程略,抛物线C的方程为x2=4y.
2)抛物线C的方程为x2=4y,即,求导得.设A(x1,y1),B(x2,y2)(其中),则切线PA,PB的斜率分别为,,从而切线PA的方程为

同理可得切线PB的方程为
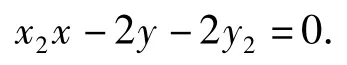
因为切线PA,PB均过点P(x0,y0),所以
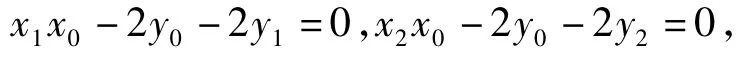
从而(x1,y1),(x2,y2)为方程x0x-2y-2y0=0的2组解,因此直线AB的方程为
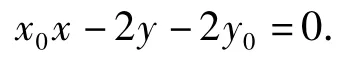
由上述解题过程知,当圆换成抛物线时,解法1和解法3仍然适用,而解法2则不适用.切点弦问题在高考试题中很常见,如:
例2抛物线C1:x2=4y,C2:x2=-2py(其中p>0).点M(x0,y0)在抛物线C2上,过点M作C1的切线,切点为A,B(当M为原点O时,A,B重合于点O).当时,切线MA的斜率为
1)求p的值;
2)当M在C2上运动时,求线段AB中点N的轨迹方程(当A,B重合于点O时,中点为O).
(2013年辽宁省数学高考试题)
解1)p=2(过程略).
2)同例1的解法得到切点弦AB的方程为
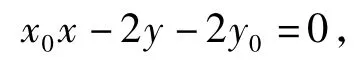
联立x0x-2y-2y0=0与x2=4y得
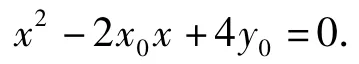
设N(x,y),由点N为AB的中点,得

由点N在直线AB上,得

由点M在C2上,得

式(1),式(2),式(3)消x0,y0,得,从而AB中点N的轨迹方程为
与参考答案相比,该解法思路简单,易于掌握.同样地,该题求切点弦AB的方程时,只适用于解法1和解法3.
例3设点P(x0,y0)在直线x=m(其中y≠m,0<m<1)上,过点P作双曲线x2-y2=1的2条切线PA,PB,切点为A,B,定点
1)略;
2)求证:点A,M,B共线.
证明设A(x1,y1),B(x2,y2),切线PA的方程为

同理可得PB的方程为
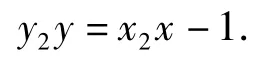
又P(m,y0)在PA,PB上,得
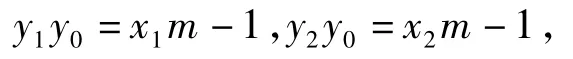
即点A(x1,y1),B(x2,y2)都在直线y0y=mx-1上,亦即AB的方程为
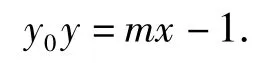
说明这里主要是求切点弦的问题.我们发现,不仅解法2不适用,解法1也不适用,因为没有办法直接求斜率,所以必须利用解法3的思路求解.
3 不同解法比较及求解策略
首先,从难度来看,解法1的难点在于先求2个切点P,Q处的切线方程,再利用点A(x0,y0)在切线上直接得到切点弦方程.解法2的难点在于: 1)能看出点P,Q在以AO为直径的圆上;2)能顺利写出圆的方程;3)注意到PQ是2个圆的公共弦,由2个圆方程相减得到直线PQ的方程.解法3与解法1的区别是:解法3没有直接写出斜率,利用一元二次方程根的判别式Δ=0求出斜率,其他相同.因此3种解法难度差不多,即便是圆的一般位置,处理起来也没有多大区别.
其次,从适用范围来看,解法1或解法3不仅适用于直线和圆相切时切点弦的求法,也适用于直线与一般的圆锥曲线相切时切点弦的求法;解法2仅适用于直线和圆相切时切点弦的求法.
因此,在求二次曲线的切点弦问题时,可遵循以下要求:若过圆外一点作圆的切线,则3种解法都可以,只是解法1和解法2相对简洁一点.若过一般的二次曲线外一点作曲线的切线,则要具体情况具体对待,能直接求切点处斜率的,按照解法1的思路即可;不能直接求切点处斜率的,则要按照解法3的思路,联立方程组,消元后由Δ=0求斜率.再由曲线外一点是2条切线的公共点,写出切点弦方程.
读者可以做下面2道练习题,从中进一步体会3种解法适用范围的不同.
练习1过点(3,1)作圆(x-1)2+y2=1的2条切线,切点分别为A,B,则直线AB的方程为()
A.2x+y-3=0 B.2x-y-3=0
C.4x-y-3=0 D.4x+y-3=0
(2013年辽宁省数学高考理科试题第9题)
(3种解法均可,答案为A.)
(本题是由2014年“华约”自主招生试题改编而成的,只有解法3适用,切点弦AB的方程为,答案为)
4 高等数学背景
曲线切点弦问题的知识背景是高等数学中圆锥曲线的极点和极线问题.
已知圆锥曲线C:Ax2+Cy2+2Dx+2Ey+F=0(其中A2+C2≠0),则称点P(x0,y0)和直线l: Ax0x+Cy0y+D(x+x0)+E(y+y0)+F=0是圆锥曲线的一对极点和极线.
若极点在曲线C上,则极线l就是曲线C在点P处的切线;若过极点可作曲线C的2条切线,P,Q为切点,则极线就是直线PQ.若利用极点和极线的有关性质,则可以直接写出切点弦方程.
如本文开始的引例,极点A(x0,y0)相应的极线方程为x0x+y0y=r2,即为切点弦PQ的方程.例1中曲线C:x2=4y,极点A(x0,y0)相应的极线方程为
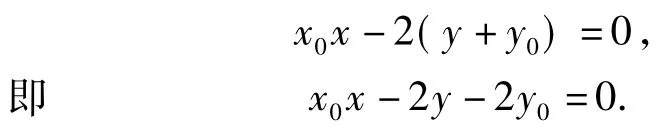
例2同例1(解法略).例3中曲线C:x2-y2=1,极点P(m,y0)相应的极线方程为
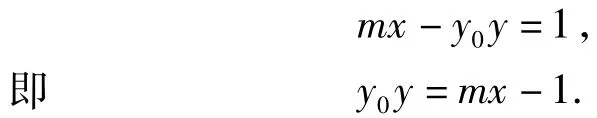
5 结束语
通过上面的分析可以发现,解法2(即新教材的处理方法)是最特殊的解法,只能适用于直线与圆相切的问题.解法1比解法2适用范围更广,只要切点的斜率能求即可,如文献[1]中的2个题目和本文的例1、例2.解法3的适用范围最广,只要是直线与二次曲线相切的问题,都可以求解.因此,这3种解法之间是特殊与一般的关系,我们要正确看待特殊方法与一般方法的关系.不仅要通过研究教材例题和习题,寻求解决一个问题的最优途径,更要透过现象看本质,寻求一类问题的普遍适用的解决方法,让学生能触类旁通,举一反三.
教材是教学的出发点和归宿,教师在教学中既不能全盘否定教材,另起炉灶,也不能过分盲从、迷信教材的权威,照本宣科.要有自己的理解和思考,用批判的眼光看待教材,创造性地使用教材.只有这样,我们的课堂教学才会充满生机和活力.
作为学生,无需知道曲线切点弦的高等数学知识背景,必须利用他们所掌握的知识方法解决问题.但作为教师,不仅要知道切点弦问题的不同解法,以及解法的适用范围,更要知道方法所隐含的高等数学知识背景.教师要有一桶水,才能给学生一杯水,才能轻松自如,举重若轻.
[1]李秀元.从一道测试题到自主招生考试题[J].中学数学教学参考:上旬,2014(7):25-26.
