“接地气”──例析“恒成立与存在性问题”的教、学、考
2015-12-05李兆江曹甸高级中学江苏宝应225803
●李兆江(曹甸高级中学江苏宝应225803)
“接地气”──例析“恒成立与存在性问题”的教、学、考
●李兆江(曹甸高级中学江苏宝应225803)
新一轮课程改革,新教材在“常用逻辑用语”一章中新增了“全称量词与存在量词”一节,它是“恒成立与存在性问题”的逻辑基础,为“恒成立与存在性问题”名正言顺地步入高考提供了依据.
因考而教,因考而研,这是一线教师一直的工作质态.因“恒成立与存在性问题”成为近几年数学高考的热点,笔者也用当下流行的3个字:“接地气”,探析“恒成立与存在性问题”的教、学、考这3个方面的“接地气”状况.
1 回归本源,遵循课改理念“接地气”
数学是一门逻辑性很强的学科,几乎处处涉及逻辑分析.日常生活中,无论是进行思考、交流,还是从事各项工作,都需要运用逻辑用语表达自己的思维.新课程总结性地安排“常用逻辑用语”学习,意在增强学生“双基”,培养学生的数学素养,从而全面提高学生分析问题、解决问题的能力.就“全称量词与存在量词”一节而言,课本中给出全称命题、存在命题的定义是:∀x∈M,p(x);∃x∈M,P(x).语言是如此精炼、简洁,但它蕴含的意义却博广精深.新课改理念意在关注它的统领作用,这就要求一线教师认真研读课本、回归知识本源、遵循课改理念实施教学,才能“接地气”,才能让学生学得融会贯通.
实质上,中学的数学概念中,与全称量词、存在量词相关的概念比比皆是.如A⊂B,是指∀x∈A,则x∈B,且∃x0∈B但x0∉A.函数是用全称量词与存在量词来定义,在下述案例中将提及.单调增函数是指y=f(x)的定义域为A,区间I⊆A,对∀x1,x2∈I,当x1<x2时,f(x1)-f(x2)<0恒成立.
例1已知函数f(x)=x2+mx-1,若对于任意的x∈[m,m+1],都有f(x)<0成立,则实数m的取值范围是______.
(2014年江苏省理科数学高考试题第10题)
若真正理解子集概念中蕴含的全称量词,则此题可改为:已知集合A=[m,m+1],,若,则实数m 的取值范围是______.
此案例另一分析视角将在下面谈到.
2 领悟本质,合理优化求解“接地气”
例2设函数f(x)=ax3-3x+1(其中x∈R),若对于任意x∈[-1,1],都有f(x)≥0成立,则实数a 的值为______.
(2008年江苏省数学高考试题第14题)
此题是含参的不等式恒成立问题,是确定参数值,而不是求参数范围,设问新颖,赢得一线教师一片赞誉.考后,笔者私下和部分考生交流后发现,在限时作答的高考考场上,能做出答案的大多数学生的思维模模糊糊,在区间[-1,1]上赋多个值,夹出实数.
应当说,学生的解法是悟到了恒成立问题的本质,是对常规解法进行合理优化而得,是“接地气”的.
合理、精炼的赋值如下:
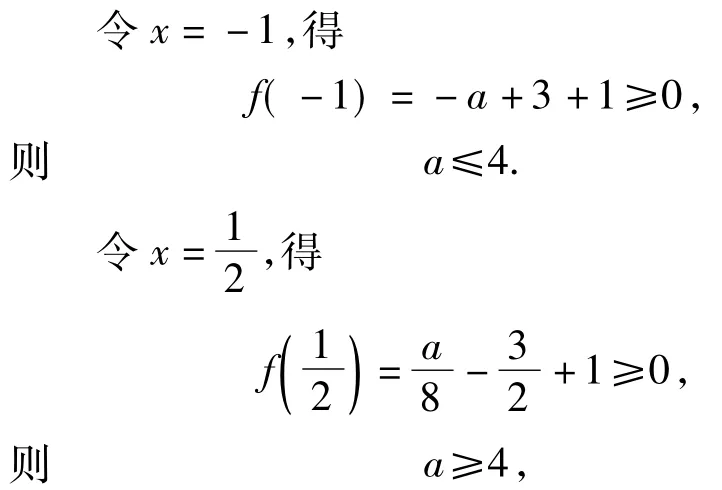
从而实数的值为4.
此后的几年高考复习中,无论是复习资料还是课堂,选用此题作为典型例题教学的随处可见,价值取向也各不相同.大多是结合其他省份高考试题中出现的恒成立与存在性问题(此处不再罗列),对参变量a进行分类讨论,求f(x)最小值.更风靡的解法是实施变量分离,将问题转化为a≥g(x)恒成立,求解a≥g(x)max,若是存在性问题,则求解a≥g(x)min.有的着眼于此题位置特征,是填空题中的压轴,分析求最值由深入繁,仅就题论题用赋值法,从而失去赋值思想在解决问题中的一般功效.实际上,采用赋值的方法可以有理有据地作出解答.分析如下:
令x=-1,得
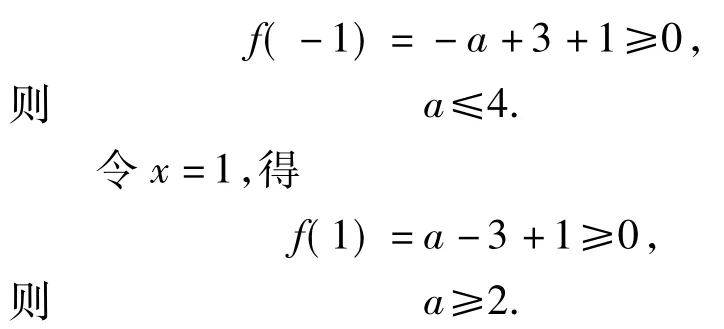
此时,可得必要条件2≤a≤4,在此必要条件下寻求充分条件.
由题意知,除端点函数值非负外,还要保证在区间[-1,1]上极值非负.由f'(x)=3ax2-3=0解得(舍去负值),则

此时f(x)的极小值为,
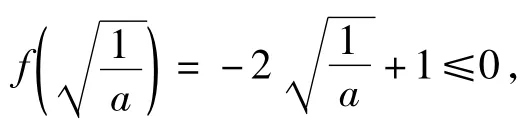
且没有其他适合条件的a值.若作为解答题,考虑到解决问题的严谨性,至多再加上“经检验”,应该说是完美的解答.
用赋值法解决恒成立问题,是“接地气”的解法,与课本上全称命题定义的本质相一致.“接地气”看待赋值法,它应是解决问题的一个常规武器,如解决抽象函数问题,曲线恒过定点问题,确定三角诱导公式中的符号问题,作立体图形截面问题[3]等等.从策略层面看,在解决一个难题时,可先对问题作简单化、特殊化、具体化、极端化处理,进而寻求问题的本源,进行严谨求解,这是赋值法本质的另一面.福建师范大学卢正勇教授在“怎样提高解题能力”一文中,对一个陌生问题的探究分析总结为5步,即:简化、观察、试探、反求、交并,赋值的作用在这5个步骤中展现得淋漓尽致[2].从培养学生能力、素养方面看,先从充分性或必要性入手,再从必要性、充分性弥补,从而化解一个复杂问题,正是彰显数学机智,提高解题能力,增强数学素质的一个有效途径.近年来从这个角度命题的高考试题屡见不鲜.
3 透视学情,完善认知缺失“接地气”
例3设a1,d为实数,首项为a1,公差为d的等差数列{an}的前n项和为Sn,S5S6+15=0,求d的取值范围.
这个问题是高考复习中的典型问题,典型体现在问题的性价比高,是训练学生思维能力的良好素材.复习资料提供的简答如下:
由等差数列前n项和公式,知S5S6+15=0可转化为
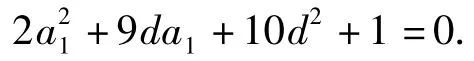
由题意知,存在a1∈R,使等式成立,从而由Δ≥0得
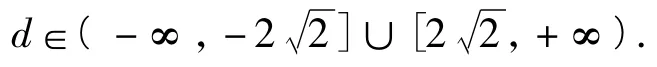
笔者曾在课堂上留有充裕的时间让学生独立思考此题并与不同类型学生交流,力争寻找难点的症结.部分学生虽能向上述参考答案方向转化,但对a1的范围有疑虑,认为应将问题转化为关于a1的方程在某区间上有解,导致思路无功而返.更多的学生是向求函数值域方向转化.先将等量关系视为关于d的一元二次方程,由,解得作为函数的定义域.再将上述等量关系转化为函数关系
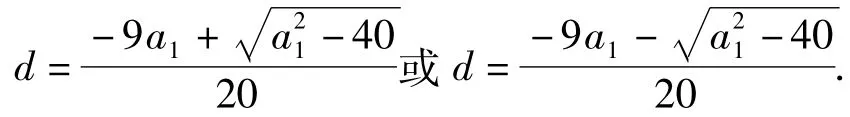
2个变量,靠一个等量关系互相依存,不能向方程转化,而向函数转化,致使思路过于曲折.一方面是受函数关系的影响根深蒂固,即,对集合A中的任一元素,在法则f作用下,集合B中存在唯一确定的元素与之对应.换一种说法就是,函数是通过2个量词“任意”、“唯一”,一个等量关系,刻画2个变量的依存关系.另一方面,是受当前比较盛行的题型:“方程在某区间上有解,转化为函数求值域”影响,出现严重的思维定势,导致题意理解方面顾此失彼,把握不住重点,误将题中的条件“设a1,d为实数”当成解决问题的大前提.由,解得作为函数的定义域,是明显的思维回路.
学生不能优化求解的另一原因是不能在新的设问情景中理解存在性问题.题目是以数列为背景的,无“存在”字样,由等量关系中的“存在”创设关于d的不等量关系.实质上,不等量关系相对于等量关系是普遍存在的.因a1,d为实数,至于存在多少,是什么,都无关紧要.此处给出其中另一常规解法.
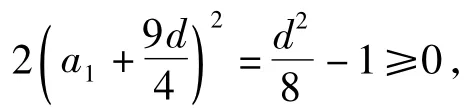
从形的角度分析,可以通过旋转变换向圆锥曲线转化,这已超出学生的知识范畴,此处不赘述.
这里,笔者就学生独立处理无字眼提醒的存在性问题,出现的各种思维偏差作探讨,意在表明:一线教师的教学应透过那些机械操作的问题,不断发展、不断更新.由学生的认知需求出发,系统完善学生的认知缺失,引导学生从问题本质着手,活学活用,弄清它们的内在联系,体会它们是如何互相转化的.值得关注的是,课堂上,学生是主体,教师是主导,教师的工作对象是学生,从学生的认知需求出发,才能“接地气”,才能切实提升课堂效率.
4 考查合理,提供正确导向“接地气”
在近几年江苏省数学高考中,无论是填空题还是解答题,恒成立与存在性问题频繁出现,其呈现方式,考查理念也是各不相同.如2008年的第14题、第18题以直线与圆为背景,给出“与其坐标无关”;2009年第18题仍以直线与圆为背景,给出“无穷多对”;2010年第18题和2011年第18题均以直线与椭圆为背景,给出“任意”、“必过定点”、“与m无关”;2011年第19题以数列为背景,给出“任意、都成立”字样;2011年第19题以函数为背景,给出“恒成立”字样;2012年第17题以应用题为背景,给出“可以”字样;2013年第19题以数列为背景,考查恒成立问题.没有全称量词提醒的字眼,对考生能力提出较高要求.在平时的教与学过程中,若不注重“接地气”,而是浮于表面,是很难准确求解的.
由上述可知,自实行新高考以来,恒成立与存在性问题都是作为中档偏难题呈现的,其呈现的背景、方式也多种多样,对学生的能力与素养作了较好的考查,很好地反映出这2个知识点的价值.2014年的江苏高考试卷中,仍有3个重要位置出现恒成立与存在性问题,而且都有明显的字眼.立意是从形的角度考查恒成问题,但背景是老教材中二次方程根的讨论问题,要求在区间[m,m+1]的2侧各有1个根,即江苏新课程无论是教学要求还是考试说明,对二次方程根的讨论问题都大大削弱要求,取而代之的是以函数的零点知识呈现,意在让学生真正领悟函数、方程、不等式的有机联系.
以这样的背景呈现问题,是否会滋生新课改下“穿新鞋,走老路”的做法.第19题第3)小题以存在性设问,考查比较大小,第2)小题是变量分离方法解决的恒成立问题,当然用换元、合理赋值、检验说明3个步骤更是轻松求解.总体看待第1),2)小题,在高考试卷中这样的位置出现这样的问题,意在送分,但送分也应讲究送法,不合理的送分可能会引导平时教学“搞题型、套路”、“搞题海战”等违背学生身心发展的事.第20题第3)小题,以数列为背景,综合“任意”、“存在”,考查构造法解决问题.构造的逻辑基础仍是存在性问题,不应单靠逻辑严谨推理,应先赋予特殊再考虑充要的说明,这样有序化解难点,问题就能迎刃而解.
结束语:“接地气”说白了就是要广泛接触学生,反映不同类型学生的认知状况.教师不能让自己高高在上,凭借自己的认知盲目行事而脱离了学生的认知需求,要遵循教与学的规律,要关注学生的终身发展.不是浮于表面,而是踏踏实实,深入教材,从知识方法的本质实施教学.当然,高考也应起到良好的导向作用.只有教、学、考这3个方面形成合力,学生的思维水平、数学素养方能全面提升,从而达成数学新课程的培养目标.
[1]中华人民共和国教育部制订.普通高中数学课程标准(实验)[M].北京:人民教育出版社,2003.
[2]罗增儒.数学解题学引论[M].西安:陕西师范大学出版社,2008:79-81.
[3]李左杰.赋值法在作截面交线中的应用[J].中学教研(数学),2012(11):16-18.
[4]吴洪生.将参数合理定位让学生勇敢面对──近年高考“存在性、恒成立问题”中的参数解读[J].中学数学教学参考,2014(6): 49-50.
