基于D-S证据理论的飞行事故预测模型

2015-12-05薛明浩端木京顺甘旭升闵桂龙

安全与环境工程 2015年3期

薛明浩，端木京顺，甘旭升，闵桂龙

（1.空军工程大学装备管理与安全工程学院，陕西西安 710051；2.空军工程大学空管领航学院，陕西西安 710051）

飞行事故预测是在对历史数据统计和分析的基础上，对未来可能发生的飞行事故预先做出近乎合理的推测判断［1］。准确的飞行事故预测可以为飞行安全管理提供帮助，对有效地预防飞行事故具有十分重要的意义。

针对飞行事故预测国内外学者已做了大量的研究［2-3］。如灰色预测法［4］、时间序列［5］一般是选取某种函数建立相关数学模型，并通过历史数据对数学模型进行修正，然后利用模型进行预测，但预测模型收敛性、精度等均受到不同程度的限制；神经网络（BP）［6-7］具有很强的非线性映射能力，可以弥补传统方法的不足，但也存在易陷入局部极小点和过拟合等缺点，使得其应用受到限制；最小二乘支持向量机（LS-SVM）［8］较好地解决了小样本、非线性、局部极小点等问题，但求解时存在二次规划问题，求解速度相对较慢。基于此，本文针对单个预测模型存在不同缺点以及难以达到理想预测精度的问题，提出一种基于证据理论的飞行事故组合预测模型，分别采用时间序列、BP神经网络和支持向量机对飞行事故进行预测，根据每个模型的相对误差确定该模型在组合中的权重，从而确立基本信任分配函数，并运用D-S证据理论［9］对函数进行融合，进而对未来的飞行事故发生情况进行预测。

1 三种预测模型

1.1 时间序列预测模型

时间序列预测模型就是将预测对象时间序列反映的发展过程和趋势进行类推，以预测其未来可能达到的水平。时间序列预测模型主要包括稳定模型和非稳定模型，由于飞行事故存在一定的周期波动，其时间序列通常属于非稳定模型，因此这里采用差分自回归滑动平均法（Auto Regressive Integrated Moving Average，ARIMA）模型［10］，其模型表达式为

式中：Yt为t 时刻的实际值；α 为参数，α=τ（1-φ1-φ2-φp），其中τ=E（Yt）；εt为t 时刻的随机误差；p、q分别为自回归阶数和滑动平均阶数；φ1，φ2，…，φp为自回归参数；θ1，θ2，…，θq为滑动平均参数。

对于飞行事故，ARIMA 模型建模主要过程有模型识别、平稳化处理、参数估计和模型检验等，具体步骤如下：

（1）通过对时间序列的分布图、自相关函数的分析，对时间序列的平稳性进行识别。

（2）通过对非平稳序列的差分变换使非平稳序列转化为平稳时间序列。

（3）通过赤池信息量准则（Akaike’s Information Criterion，AIC）来确定ARMA 模型阶数p 和q。AIC准则函数为

（4）估计模型的未知参数，并检验参数的显著性及模型本身的合理性。

（5）将历史数据代入模型，以验证模型是否有效；否则，转入第（3）步。

（6）利用所建立模型进行预测分析。

1.2 BP神经网络预测模型

BP神经网络是一种基于误差逆向传播算法训练的多层前馈网络，但算法存在收敛速度慢、容易陷入局部最优以及网络性能差等缺点。针对以上缺点，采用分组批处理的训练方式，不仅可使不同学习率在训练样本循环训练完成后得到适当调整，又能减小调整学习率的时间，从而加快收敛速度；将每个训练样本的梯度值平均在一起，以获得更精确、更符合全局的梯度估计和较好的泛化能力；使用复合误差函数Gλ（m）来代替传统算法中的全局均方误差函数E（m），以此来加快收敛速度和减小陷入局部最优的可能性；采用分开调整输出层学习率β1 和隐含层学习率β2 的方法替代传统算法中固定不变的学习率β［11］。

分组批处理的训练方式中，对于各分组Pi（1≤i≤n）个训练样本，BP 神经网络实际输出值（）与理想输出值）间的全局均方误差函数可表示为

复合误差函数Gλ（m）的具体展开式为

式中：λ=exp（-｜ΔE（m）｜／E（m）），其中ΔE（m）为误差变化量，ΔE（m）=E（m）-E（m-1），E（m）为分组样本在第m 次循环学习时的全局均方误差。

1.3 最小二乘支持向量机预测模型

最小二乘支持向量机（LS-SVM）是支持向量机的一种拓展，它适用于飞行事故预测这样的小样本情况，使用最小二乘支持向量机模型进行飞行事故预测就是将已有的飞行事故数据作为输入值，经过变换，得到学习样本，建立预测模型，从而预测未来时刻飞行事故的预测值。其关键问题在于如何重构线性空间，找到输入与输出的对应关系。

设训练样本为｛（x1，y2），…，（xm，ym）｝，xi∈Rm，yi∈R（i=1，2，…，m，m 为训练样本个数）。将训练样本映射到高维特征空间，并采用如下的回归估计函数对该空间进行线性回归：

式中：w 为权值向量；b 为偏差；φ（x）为从输入空间到高维特征空间的非线性映射。

基于结构风险最小化原则，可将回归问题等效为如下的约束优化问题：

s.t.yi=wTφ（xi）+b（i=1，2，…，m）

式中：c为正规化参数；ξ为非相关随机误差。

用Lagrange方法求解该优化问题，可得

式中：α为Lagrange乘子，α=［α1，α2，…，αm］。

根据Mercer条件，选用RBF核函数，利用最小二乘法可求出回归估计函数：

式中：σ为核宽度。

由此可见，LS-SVM 预测模型仅需要确定正规化参数c和σ，而其最优参数组合在实际运用时应根据需要来确定。

2 证据理论相关概念及预测模型

2.1 D-S证据理论基础

定义1 设Θ 为识别框架，∀X⊆Θ，m（X）表示用［0，1］区间上一个确定值来赋予2Θ中每一个元素，即m（X）：2Θ→［0，1］，满足：

式中：m（X）为事件X 的基本信任分配函数，它表示证据对X 的信任程度。

D-S证据理论相较于其他评价方法最大的优势是能将不同评价结论实施合成。设在识别框Θ 上有2个证据是完全独立的基本可信函数，分别为m1和m2，对应焦元为，则D-S合成算法规则为［9］

式中：C 表示合成后的函数，若待合成的函数多于2个，则可通过上述方法将之前的合成结果与下一个函数再次合成，直至所有函数完成合成，这种方法便于将不同的预测模型进行融合。

2.2 基于D-S证据理论的飞行事故组合预测模型

假设历史飞行事故率通过预测模型进行训练后，每个模型产生的预测误差为（i=1，2，3），其中为飞行事故率的预测值，yi为飞行事故率的实际值，在对各个预测模型进行融合之前，需要提取各个待融合模型的权重。在飞行事故预测模型中，各个预测模型的权重被视为证据理论的基本信度值，其对应的信度值（i=1，2，3）。而权重的确定又与预测精度有密切的关系，预测精度高，则该算法在组合中所占的权重大；预测精度低，相应的权重就小。因此，权重ωi可表示为关于ei的函数：

为避免某种预测模型出现相对误差为0 的情况，这里引入ε，ε=0.000 1，进而可得到组合预测结果：Y==1。所以，基于D-S证据理论权重融合的飞行事故率预测的具体流程如下（见图1）：

（1）选择预测模型的输入变量和输出变量，并对输入样本做相应的预处理。例如对于时间序列预测模型，飞行事故率本身就是一维时间序列，其中历史飞行事故率为自变量，待测飞行事故率为因变量；而对于BP神经网络和最小二乘支持向量机，需要将一维历史数据转化为矩阵形式，以获得数据的关联信息；此外，为了加快样本训练速度和模型的收敛速度，提高模型预测精度，还可以采用归一化方法对数据进行如下预处理：

（2）将处理完的数据作为输入量，分别采用三种预测模型对a—b年份的飞行事故率进行预测，计算各模型的相对误差，并采用平均绝对百分比误差（MAPE）来评价预测模型的预测效果，其表达式为

（3）根据计算得到的各个预测模型的相对误差，运用D-S合成法测，计算各模型的权重wi，这里选取待测年份前三年的预测结果作为融合样本。

（4）利用权重融合模型求得的各模型权重，可得出三种预测模型融合后最终的输出值。

3 实例分析

飞行事故万时率作为飞行安全水平的重要指标，一方面是飞行员素质、飞机可靠性、训练水平以及飞行安全管理工作好坏的综合表现，另一方面也是衡量空军战斗力强弱的重要标志。因此，本文选取美国空军1988—2010年的飞行事故万时率［12-13］作为预测模型研究的基础数据（见表1），并基于D-S证据理论融合模型对待测年份的飞行事故率进行预测，具体过程如下：

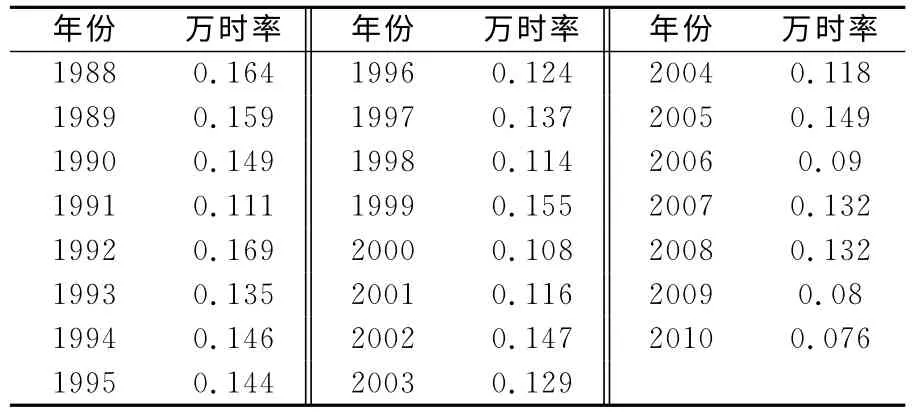
表1 美国空军1988—2010年飞行事故万时率Table 1 10 000hour-rates of flight accidents in United States Air Force from 1988to 2010

（1）采用时间序列模型对1988—2010 年的飞行事故万时率进行预测，并计算相对误差。建模前先利用EViews软件对1988—2010 年飞行事故万时率时间序列模型进行ADF单位根检验（见表2），检验结果表明ADF 检验t-统计量为-0.591 073（远大于1%、5%、10%的检验临界值），故为非平稳序列，印证了之前根据事故率为非平稳序列而采用差分自回归滑动平均法的判断。因此，需将原有的非平稳序列转换为平稳序列后才能进行预测，而通过一阶差分变换后ADF 单位根检验结果（见表3）显示ADF检验t-统计量为-6.601 631（小于1%、5%、10%的检验临界值），表明差分后的时间序列为平稳序列，可以对时间序列进行ARMA 建模。根据AIC准则，预测模型的自相关函数滞后数p 和偏相关函数滞后数q 都取4［14］，利用EViews软件，可得到2007—2009年飞行事故万时率时间序列模型的预测值及相对误差，见表4。

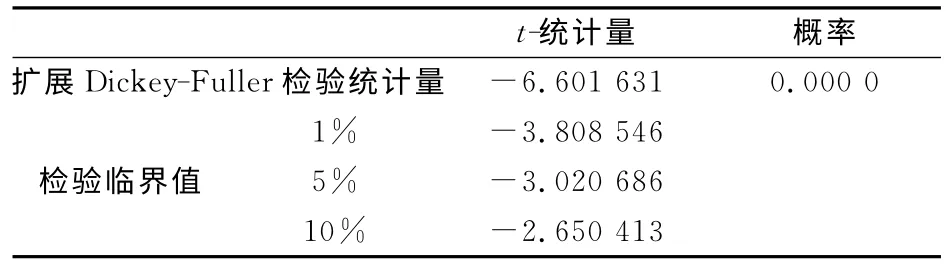
表3 一阶差分后的ADF单位根检验结果Table 3 ADF unit roots test results of first-order difference

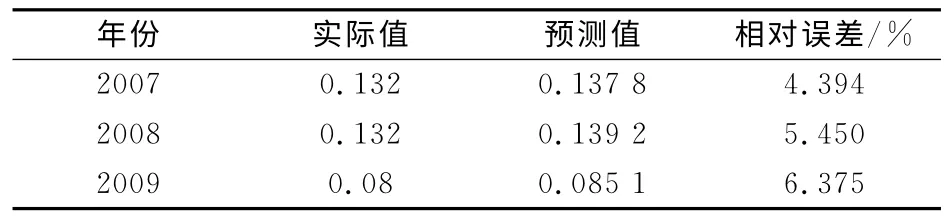
表4 2007—2009年飞行事故万时率时间序列模型预测值与实际值的比较Table 4 Actual and predicted values of time series of flight accidents from 2007to 2009

（2）分别采用BP神经网络模型和最小二乘支持向量机模型（LS-SVM 模型）对2007—2009年的飞行事故万时率进行预测，并计算相对误差。其输入及输出数据采用相空间重构方法获得，这里嵌入维数取5，延迟时间取1，可以得到2007—2009年的飞行事故万时率BP神经网络和最小二乘支持向量机模型的预测值及相对误差，见表5。

（3）根据各模型的相对误差，通过权重提取模型，可以分别得到2007—2009年三种预测模型对应的权重，见表6。

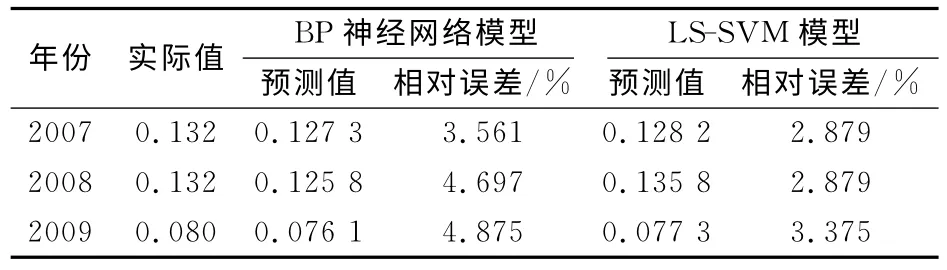
表5 2007—2009年飞行事故万时率BP神经网络和LS-SVM 模型预测值与实际值的比较Table 5 Comparison of actual values and predicted values of BP neural network and LS-SVM from 2007to 2009

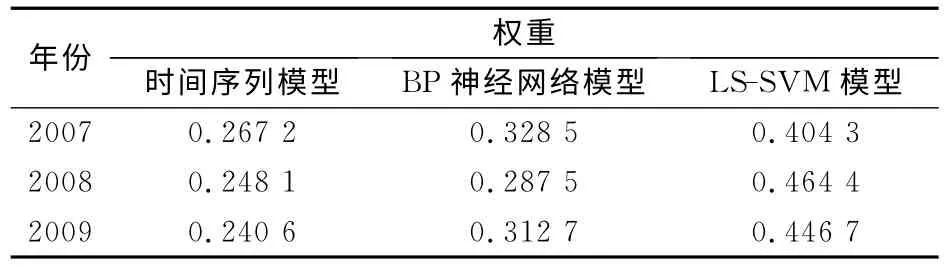
表6 2007—2009年三种预测模型对应的权重Table 6 Weights of the 3prediction models from 2007 to 2009

（4）将求出的各模型对应权重当作相应的基本信任分配函数，通过Dempster合成法则进行二重融合，得到最终的权重为0.123 4、0.228 3、0.648 3，最后对2010年度的飞行事故万时率进行预测，其预测结果见表7。由表7 可以看出，在2007—2010年飞行事故万时率的预测值中，采用DS证据理论融合模型（DS模型）的预测值的平均绝对百分比误差MAPE值（1.954%）小于任何一个单一预测模型，表明组合模型的预测精度优于其中任一单一预测模型，且预测值与实际值非常接近，具有较高的预测精度。

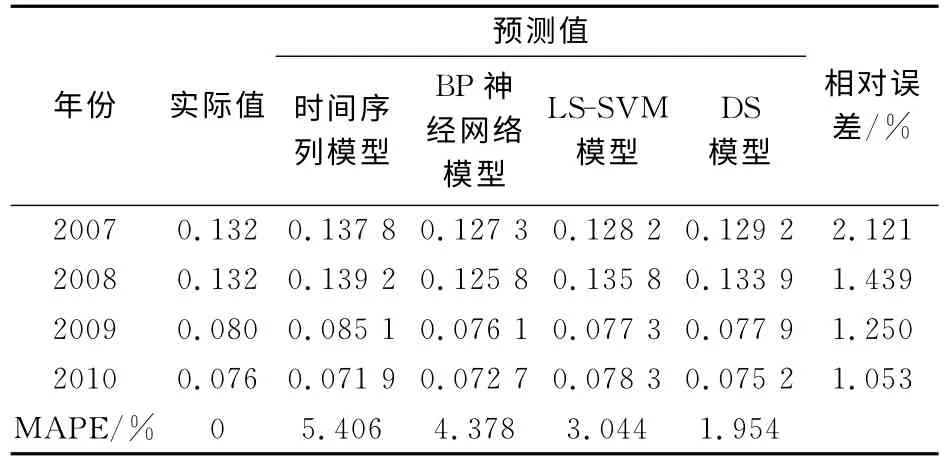
表7 2007—2010年飞行事故万时率四种预测模型预测值与实际值的比较Table 7 Comparison of actual values and predicted values of 4prediction models from 2007to 2010

4 结论

为了进一步提高飞行事故预测精度，本文通过三种预测模型对待测年份前3年的飞行事故率进行预测，根据得出的各模型预测值与实际值的相对误差，利用D-S证据理论对三种预测模型进行融合，计算出融合后各模型的权重，进而对待测年份的飞行事故率进行预测。实例研究结果表明，采用D-S证据理论融合后的预测模型的预测结果比任何单一预测模型的精度都高，且融合过程简单易行，为飞行事故预测提供了一种新的有效方法。

［1］徐邦年.飞行安全评估概论［M］.北京：蓝天出版社，2005.

［2］王永刚，单方方，王灿敏.GREAM 法在机务维修操作差错概率预测中的应用［J］.安全与环境工程，2014，21（1）：134-137.

［3］刘玲莉，孙亚菲，郑红运.基于集对分析的民航运输事故征候预测模型研究［J］.安全与环境工程，2013，20（5）：154-158.

［4］甘旭升，端木京顺，卢永祥.灰色均生函数模型及其在航空装备事故预测中的应用［J］.中国安全科学学报，2010，20（6）：40-44.

［5］Box G E P，Jenkins G M，Reinsel G C.Time Series Analysis Forecasting and Control［M］.Englewood Cliffs，New Jersey：Prentice-Hall，Inc.，1994：126-131.

［6］李瑞荣，康锐.基于神经网络的故障率预测方法［J］.航空学报，2008，29（2）：357-363.

［7］赵录峰，端木京顺，韩卫刚，等.基于改进型BP神经网络模型的飞行事故预测研究［J］.舫空维修与工程，2008（4）：25-26.

［8］Suykens J A K，Gestel V T，Brabanter J De，et al.Least Squares Support Vector Machines［M］.Singapore：World Scientific，2002.

［9］段新生.证据理论与决策、人工智能［M］.北京：中国人民大学出版社，1993.

［10］Shafer G.A Mathematical Theory of Evidence［M］.Princeton：Princeton University Press，1976.

［11］张国翊，胡铮.改进BP神经网络模型及其稳定性分析［J］.中南大学学报（自然科学版），2011，42（1）：115-123.

［12］陆惠良.军事飞行事故研究［M］.北京：国防工业出版社，2003：7-10.