基于BN 的模糊系统事故风险管理辅助分析

易玉枚，廖可兵，易灿南

（湖南工学院安全与环境工程学院，湖南 衡阳 421002）

事故分析在事故风险管理中占有非常重要的位置，各种意外事故频频发生，造成重大的人员伤亡和财产损失，为了及时预防事故发生，降低事故损失，国内外工程人员越来越重视事故的风险管理。工业生产系统在实际运行过程中存在局部故障、局部正常的状态，因而基本事件的概率存在很大的模糊性和不确定性，这里把组成单元的可靠性指标存在很大误差的系统或者是无法大量获得事故发生概率的系统或者是因为人因失效、共因失效等导致基本事件发生概率不断波动的系统称为工业事故模糊系统［1］。由于模糊系统的模糊性，对其事故系统进行定量风险管理，提高安全投入的经济性和事故风险管理相关决策的科学性及合理性，从而减少决策的风险性显得更加重要。

国内外一些学者从不同方面对事故风险管理进行了深入研究，如骆珣等［2］归纳了国内外事故风险评估方法，将其分为定性和定量两种方法，定性评估方法主要包括专家打分法、风险矩阵图分析法、外推法等，定量评估方法主要包括概率分析法、决策树法、故障树分析法、蒙特卡洛模拟等。但采用传统的分析方法对模糊系统事故进行分析仅局限在定性层次，且当前事故的风险管理主要偏重于事前管理，一旦发生事故，往往急于组织专家集中讨论处理方案，可能会延误事故处理的最佳时间。近年来，国内外学者在这些方法的改进及多种方法相结合的综合应用方面做了不少研究［1，3-7］，如Brito等［8］将多属 性效用理论应用到风险管理中；Cana［9］等尝试利用系统建模方式进行风险的智能评估。

贝叶斯网络近年来被广泛应用在数据挖掘技术、决策分析、设备诊断和风险管理等领域［10］。如马德仲等［11］将贝叶斯网络用于地下空间火灾风险评估；张立茂等［12］提出基于贝叶斯网络的复杂工程安全管理决策支持方法；徐格宁等［13］将贝叶斯网络用于汽车起重机液压系统的可靠性评估。

本文依据模糊数学的思想，把难以得到精确值的概率处理为一个模糊数，用模糊概率来表征致险因子的概率，将贝叶斯网络和三角模糊数相结合，通过建立基于贝叶斯网络的模糊系统事故风险管理辅助分析方法，对模糊系统进行事前、事中、事后定量分析，以为事故风险管理提供决策支持。

1 贝叶斯网络和三角模糊数

1.1 贝叶斯网络简介

贝叶斯网络（Bayesian Networks，BN）是一个有向无圈图，其中节点代表随机变量，节点间的箭头代表变量之间的直接依赖关系。每个节点都附有一个概率分布，根节点X 所附的是它的边缘分布P（X），而非根节点X 所附的是条件概率分布P（X／π（X）），其中π（X）表示变量X 的父节点集。贝叶斯网可以从定性和定量两个层面来理解，在定性层面，它用一个有向无圈图描述了变量之间的依赖关系；在定量层面，它用条件概率分布刻画了变量对其父节点的依赖关系［14］。

贝叶斯网推理是指利用贝叶斯网的结构及其条件概率表，在给定证据后计算某些节点取值的概率，贝叶斯网络的参数即各变量的概率分布，一般通过数据分析获得，也可通过专家咨询得到。概率推理和最大后验概率解释（MAP）是贝叶斯网推理的两个基本任务。根据证据变量和查询变量所扮演的因果角色的不同，概率推理有4种不同的类型：从结果到原因的诊断推理、从原因到结果的预测推理、在同一结果的不同原因之间的原因关联推理和包含多种上述类型的混合推理。贝叶斯网络不但具有这种推理功能，而且还可以对各推理要素进行定量描述，这反映在网络信念的传播与更新方面。

1.2 三角模糊数基本理论

对于模糊系统事故，大多数基本事件的概率数据难以获得，必须通过其他途径获取。三角模糊数是最简单、最重要和最常用的模糊数之一，不仅可以用于处理和表达模糊信息，还可以用于随机信息的表征，特别是在数据资料较少或精确性不高时，具有很好的适用性。将三角模糊数用在分析方法中能很好地解决被分析对象性能无法准确度量而只能用自然语言进行模糊分析的矛盾。

2 基于BN 的辅助分析方法

基于BN 的模糊系统事故风险管理辅助分析方法，实际上是将风险事件的形成与发生作为分析对象，通过预测（正向）推理、诊断（反向）推理、重要度分析等方式，动态分析各致险因子在事前、事中、事后各阶段的相互关系，为事故风险管理提供科学、及时、有效的决策支持。其分析过程分为致险机理分析、BN构建、推理分析三个阶段，具体流程见图2。

2.1 致险机理分析

事故风险管理通常是结合事故历史统计数据和专家经验，由故障假设、HAZOP等危险分析方法识别出来的发生频率较大且后果严重的事故确定为风险事件。在明确某一具体风险事件后，开始着手对该事件进行致险机理分析，确定导致该风险事件发生的影响因子。事故发生的机理往往很复杂，影响因子较多，各影响因素既可直接导致事故，又可通过其他因素间接导致事故，且因子间有着复杂的关联。致因分析时可先从直接原因入手，再分析找出事故的全部原因，对所有可能诱发风险事件的风险因素进行分析，列出可能的风险因素清单，再从全部因素中找出起主导作用的因素。

2.2 BN 构建

BN 的模型设计包括BN 结构设计和BN 参数设计。

2.2.1 BN 结构设计

以上述致险机理分析得到的主要风险因素为基础，结合领域专家经验得到风险因素间的因果关系，以风险因素作为节点变量，根据变量间的拓扑关系，将这些因素按照因果关系组织起来，形成BN 结构图，结构图中包括三类变量：目标变量、中间变量、信息变量（能够观察到的变量）。图中每个节点为一个变量，每个变量信息具有独立性，节点变量之间的有向弧线表示其因果关系，否则表示条件独立。

2.2.2 BN 参数设计

（1）确定根节点（没有父节点的节点）的先验概率。由于模糊系统的模糊性，先验概率需以人、物的故障率为基础，这方面的数据都比较缺乏或很难获得，本文采用专家评定法，并利用3σ法来表征根节点的模糊先验概率。专家评定工作由3人以上的专家小组来进行，各专家分别给出各信息变量（根节点）发生概率的估计值，取各估计概率的均值为m，方差为σ。设估计概率值服从正态统计规律，根据σ规则，它的值落在区间［u-3σ，u+3σ］的概率为99.7%，故设l=u=3σ，将各个概率值模糊表征为（3σ，m，3σ）。其中：

式中：xi表示第i项概率值（i=1，2，…，n）。

（2）确定节点之间的关系即子节点的条件概率。在建立BN 结构的基础上，网络中的每一有父节点的子节点都对应一张条件概率表（CPT），表示其与父节点之间的依赖关系。

2.3 推理分析

2.3.1 事前风险事件概率预测——预测推理

利用联合概率分布可以直接计算系统叶结点（风险事件）T 的发生概率：

其中：节点Ei（1≤i≤n-1）对应于BN 中的根节点和中间节点；ei∈｛0，1｝表示节点Ei发生与否；n 为BN 中节点的数目。

P（T=1）值的大小表明了风险事件T 发生的可能性，管理人员通过建立贝叶斯事故网络，然后根据现场情况的实时变化（致险因子的变化状况），在BN 中录入致险因子的状态值，即可预测事故发生概率，界定事故等级，尽早采取防范措施，对企业实际风险管理具有重要的指导意义。

2.3.2 致因诊断——诊断推理

致因诊断指在已知风险发生时，诊断并查明导致该风险的原因，快速查明最可能的致因组合。利用BN 的反向推理技术，叶结点T（风险事件）发生后各根节点（致险因子）的后验概率P（Xi／T=1）从事故或故障诊断角度指明了引起事故的最可能的原因，即

P（Xi／T=1）越大，表示节点i成为事故致因的概率越大。利用该推理的目的是在当风险发生时，可以及时控制并找到风险源，防止风险进一步恶化或再次发生。

2.3.3 重要度分析

对于一个事故系统来说，各致险因子在系统中的重要性对于系统安全性的改善具有十分重要的意义。由于BN 结点变量的条件独立性及其特有的双向推理优势，其条件概率包含了丰富的信息，应用BN 可以方便地计算某个致险因子发生时，叶节点发生概率的变化情况。

（1）根节点Xi发生的条件下叶结点T 发生的概率P（T／Xi=1）反映了某个致险因子状态发生的微小变化导致风险事件概率发生变化的程度，即

（2）叶结点发生后各根节点的条件概率P（Xi／T=1）也从事故诊断的角度反映了根节点在事故系统中的重要性大小。

（3）对于某个根节点，还可以求出叶结点对某个根节点的灵敏度。设F（x）=g（X）（X=x1，x2，…，xn），定义F（x）对变量x1的偏导数为F（x）对xi的灵敏度Si=∂F／∂x，Si绝对值的大小反映了F（x）随xi变化的快慢程度［15］。

根据BN 双向推理功能计算各种条件概率，根据根节点的变化对叶结点的影响程度（灵敏度分析），可以找到系统的薄弱环节，辨识关键致险因子及其控制优先次序，从而对薄弱环节致险因子进行重点预防控制，进一步减少系统风险。

3 实例分析

文献［1］中以某化工企业储油罐体为例应用FTA 模型对该企业发生火灾爆炸事故进行了分析，所建立的事故树较全面、合理，此处直接引用其致因分析及基本事件的三角模糊概率，并应用本文提出的基于BN 的模糊系统事故风险管理辅助分析方法对其火灾爆炸事故风险管理过程进行实例分析。

3.1 致险机理分析

以储油罐火灾爆炸作为风险事件，确定导致该风险事件的影响因子为：X1液体充装过量；X2压力表指示错误；X3安全阀弹簧损坏；X4安全阀选用错误；X5密封失效；X6罐体破损；X7人的误操作；X8静电积累；X9人体与化纤品摩擦；X10作业中人体与导体接触；X11未使用防爆电器；X12防爆电器损坏；X13违章吸烟；X14违章动火；X15使用铁质用品；X16穿戴铁钉的鞋；X17未设置防静电装置；X18接地电阻不符合要求；X19接地线损坏。

3.2 BN 构建

3.2.1 BN 结构设计

依据致险机理分析得出的风险因子构建BN 结构，如图3所示。

3.2.2 BN 参数设计

（1）确定根节点的先验概率。通过专家对致险因子发生的概率进行打分，再利用3σ法确定各根节点的模糊概率见表1。

（2）确定节点之间的关系。子节点与父节点之间的逻辑关系用联接强度（条件概率）表示，节点的状态描述为：Xi=若子节点与父节点的关系为逻辑与的关系，如X9、X10与其父节点C12，其联接强度如表2所示；若子节点与父节点的关系为逻辑或的关系，如X1、X2与其父节点C3，其联接强度如表3所示；若节点之间无联接，则为相互独立关系；依此确定BN 中各节点之间的关系。

表1 各根节点发生概率模糊处理数据Table 1 Processing data of the fuzzy probability of root nodes

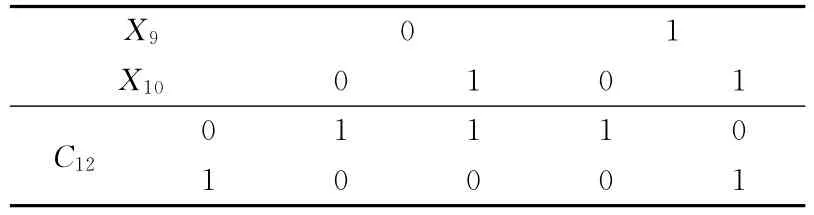
表2 逻辑与条件概率Table 2 Conditional probability of Boolean AND

表3 逻辑或条件概率Table 3 Conditional probability of Boolean OR

3.3 推理分析

3.3.1 事前风险概率预测

根据BN 的预测推理及三角模糊数的运算规则，计算得出风险事件（储油罐发生火灾爆炸事故）的概率为（0.000 067 821 6，0.000 681 492 0，0.000 067 821 6），即该企业发生储油罐火灾爆炸事故最可能的概率是0.000 681 492 0，左右波动的概率分别为0.000 067 821 6。可见，事故概率为10-4数量级，略高于交通事故死亡率，危险性中等，说明该企业储油罐存在较大风险，应立即采取措施。

此外，还可计算在任意几个根节点发生的条件下叶结点发生的概率，如X1和X5都发生的条件下，叶结点 发生的 概率为（0.023 6，0.059 0，0.023 6）。

3.3.2 致因诊断

利用BN 的反向推理技术，当储油罐发生火灾爆炸事故时，各致险因子的后验概率（最可能概率）见 表4。由 表4 可 知：X3＞X1＞X5=X7＞X6＞X14＞X12＞X15=X16＞X11＞X2＞X4＞X13＞X18＞X19＞X8＞X10＞X17＞X9，由此发现X3（安全阀弹簧损坏）是最可能导致储油罐发生火灾爆炸事故的诱因，此外X1（液体充装过量）、X5（密封失效）、X7（人的误操作）、X6（罐体破损）、X14（违章动火）、X12（防爆电器损坏）、X15（使用铁制用品）、X16（穿戴铁钉的鞋）、X11（未使用防爆电器）也是造成火灾爆炸的主要原因，隐患排查应依次主要从X3、X1、X5、X7、X6、X14、X12、X15、X16、X11入手，直至事故得到控制。

表4 叶节点发生时各根节点的后验概率Table 4 Posterior probability of root nodes when leaf nodes occur

3.3.3 重要度分析

①叶节点发生时各根节点的后验概率（见表4）从故障诊断的角度反映了元件在系统中的重要性大小；②根节点Xi发生的条件下叶结点发生的概率P（T／Xi=1）见表5，它反映了致险因子的概率重要度，其大小顺序为：X1=X2＞X5=X6=X7＞X11=X12=X13=X14=X15=X16＞X3=X4＞X8＞X9＞X17=X18=X19＞X10；③叶结点对各根节点的灵敏度见图4，其大小顺序为：S1＞S2＞S5=S7＞S6＞S14＞S12＞S15=S16＞S11＞S13＞S3＞S4＞S8＞S9＞S18＞S19＞S17＞S10。可见，灵敏度排序与概率重要度顺序一致，而且更精确。实际中，这三项指标可相互配合使用，选取各项排序结果均较为靠前的根节点作为关键致险因子，指导风险管理人员明确日常施工安全管理控制要点，进而最大程度地避免事故发生。

表5 根节点Xi发生条件下叶节点发生的概率P（T／Xi=1）Table 5 Probability of leaf nodes when root nodes occur

4 结论

（1）基于BN 的模糊系统事故风险管理辅助分析方法，可对事故风险管理全过程提供定量、动态分析，克服了模糊系统过分依赖工程师实践经验、静态分析等不足，有助于提高风险管理决策的科学性。

（2）将三角模糊数用于分析方法中可解决模糊系统因事故致险因子故障率数据缺失而无法进行定量分析的缺陷。

（3）利用BN 可以有向图形式直观表达风险事件致险因子间的不确定性关系，运用BN 推理技术能够实现正向预测推理，动态预测风险事件发生概率，提前做好事故预防工作；反向诊断推理能快速查明事故最可能的致因组合，及时控制事故的恶化；致险因子重要度、灵敏度分析，能辨识系统薄弱环节，明确风险管理过程控制重点及优先次序，从而可以针对安全生产工作的薄弱点或薄弱环节，有的放矢地采取预防措施和对策，尽量减少事故发生。

［1］王陈玉书，张园园，张巨伟.化工事故模糊系统FTA 模型的研究与应用［J］.中国安全生产科学技术，2013，9（2）：117-120.

［2］骆珣，王晓庆.项目风险评估的应用与展望［J］.现代管理科学，2006（9）：11-12.

［3］易灿南.FTA-AHP方法研究及应用［J］.中国安全生产科学技术，2013，9（11）：167-173.

［4］崔英，杨剑锋，刘文彬.基于HAZOP 和LOPA 半定量风险评估方法的研究与应用［J］.安全与环境工程，2014，21（3）：98-102.

［5］陈全，张丽婷.HAZOP-FTA 综合分析方法在煤化工装置中的应用［J］.中国安全生产科学技术，2013，9（7）：134-138.

［6］王涛.基于PHA-LEC法的油田地面工程作业场所潜在风险分析［J］.安全与环境工程，2013，20（3）：143-148.

［7］陈国兵.基于FMEA／FTA 的贝叶斯网络安全性分析方法［J］.质量与可靠性，2011（5）：21-26.

［8］Brito A J，de Almedia A T.Multi-attribute risk assessment forrisk ranking of natural gas pipeliness［J］.Reliability Engineering and System Safety，2009，94：187-198.

［9］Cana D，Cruz D A.Intergrated methodlogy for project risk management［J］.Journal of Construction Engineering and Management，2002，128（6）：473-485.

［10］Heckerman D，Mamdani A，Wellman M P.Real-world applications of Bayesian networks［J］.Communications of the ACM，1995，38（3）：24-26.

［11］马德仲，丁文飞，刘圣楠，等.基于贝叶斯网络的地下空间火灾风险评估方法研究［J］.中国安全科学学报，2013，23（11）：151-156.

［12］张立茂，陈虹宇，吴贤国.基于贝叶斯网络的复杂工程安全管理决策支持方法研究［J］.中国安全科学学报，2011，21（6）：141-146.

［13］徐格宁，李银德，杨恒，等.基于贝叶斯网络的汽车起重机液压系统的可靠性评估［J］.中国安全科学学报，2011，21（5）：90-96.

［14］张连文，郭海鹏.贝叶斯网引论［M］，北京：科学出版社，2006.

［15］Saurin V V.Shape design sensitivity analysis for fracture conditions［J］.Computers and Structures，2000，76：399-405.