基于可拓云模型的电力生产安全综合评估方法

曲朝阳，王 健，吴 云，杨杰明

（东北电力大学信息工程学院，吉林 吉林 132012）

随着电力行业的快速发展，其生产过程中的安全问题日益凸显，如何保障电力生产的安全性和可靠性成为电力企业发展中不可忽视的问题。安全评估在国际上也称之为风险评估或危险性评估，是一种有效提高电力生产安全性的现代化管理方式。在电力生产管理中应用该方法，能够对电力生产过程中的安全性进行度量、预测和评估，以此定性或定量分析可能发生的危险因素，并采取针对性的措施尽量消除生产中的隐患［1］。因此，为保障电力生产的安全性，对其进行安全综合评估是一项非常重要的工作。

目前现有的评估方法主要有模糊决策法［2］、灰色关联分析法［3］和人工神经网络法［4］等。模糊决策法主要从评估指标的模糊性角度出发进行安全评估，但其评估过程中对评估指标的主观性和随机性考虑不足。灰色关联分析法可通过一定的方法，找出各因素间的数值关联关系从而进行定量的安全评估，但评估指标不乏定性指标的存在，如何将定量与定性评估有效结合尚待进一步研究。人工神经网络法能够反映评估指标之间的内在联系，但评估过程需要大量的训练样本。近几年来，许多学者对电力生产安全综合评估问题进行了相关研究，如周姝［5］、焦晓佑等［6］、孙志禹等［7］分别从电力生产班组安全管理能力、电力安全生产文化和作业安全三个角度对电力企业生产安全进行了评估，为电力生产安全综合评估领域提供了新的思路；马丽云等［8］首次应用云重心理论对电力企业生产安全进行综合评估，实现了定性指标的定量转换，并通过用云重心的位置改变来衡量电力生产安全状况的变化，取得了较好的效果，然而仅仅使用云重心来评估，易造成部分重要信息的缺失。

针对上述问题，本文首先基于现代安全管理理论和生产实际，建立了电力生产安全综合评估指标体系，并采用集层次分析法和熵权法于一体的主客观综合赋权法确定各评估指标的综合权重［9］；然后全面兼顾电力生产安全分级边界的模糊性和随机性，并结合云模型的双重不确定推理特性和可拓学中的物元理论兼具定性、定量分析的特点，提出了一种基于可拓云模型的电力生产安全综合评估方法；最后通过算例分析验证了该方法的有效性和合理性。

1 评估指标体系的建立及权重确定

1.1 评估指标分析

电力生产安全综合评估主要是针对可能影响电力生产安全性的各指标因子所进行的综合评估，其所选指标的正确性和合理性至关重要。根据现代安全管理理论和生产实际可知，这些影响主要来自人、机、环境和管理四个方面［10］。

人是电力生产中操作的主体，人的安全性直接关系着电力生产的整体安全；机器是电力生产必不可缺的装置，其安全性不容忽视；环境是电力生产的外在因素，时刻影响着电力生产的安全；管理是电力生产安全的基石，更是电力生产安全管控的核心环节［11］。由此可见，这四方面之间相辅相成，缺一不可。

基于以上分析和现有的研究成果，本文建立了电力生产安全综合评估指标，详见表1。

1.2 指标权重的确定

为了保证权重分配的合理性，本文采用主客观综合赋权法确定评估指标的综合权重，其中采用层次分析法确定主观权重，熵权法确定客观权重，并利用加和法集成原理综合主客观权重确定指标的综合权重［12］。该方法不仅有效避免了单一赋权法的缺陷，同时实现了权重分配的主客观统一，从而保证了各指标权重系数的合理性。

表1 电力生产安全综合评估指标体系Table 1 Synthetic evaluation system of electric power production security

层次分析法是一种通过主观判断指标间的相对重要程度来确定指标权重的方法。其原理是通过专家对所有指标的重要性进行排序，确定各指标因子间的相对重要程度，并构造出判断矩阵，再依次求出各个指标的权重值wai，进而计算出指标主观权重向量Wa，即

式中：n为评估指标个数；wai为第i个评估指标的权重值。

熵权法是一种通过各评估指标对应的实际值所提供信息量的大小来客观确定指标权重的方法［13］。其原理是根据各个指标的变异程度，客观地计算出各个指标的熵值，再通过熵值大小确定各指标的客观权重值wei，进而计算出指标客观权重向量We，即

式中：n为评估指标个数；wei为第i 个评估指标的权重值。

最后，利用加和法集成原理，将主客观权重进行组合集成，可计算得到指标最终的综合权重向量W，即

假设有n个指标，则有

式中：a 为主观权重Wa对综合权重的影响程度；b为客观权重We对综合权重的影响程度；Pi为已求向量Wa升序排列后的第i个分量。

2 可拓云理论概述

2.1 云模型

云模型是由李德毅院士基于模糊集理论和概率论提出的一种反映事物或人类知识中模糊性和随机性的新理论［14］。该模型将事物本身的模糊性和随机性巧妙地集于一体，并采用固定的数学表达式加以统一描述分析。迄今为止，云模型已发展出多种分布形态，如三角形云、梯形云等，其中正态云模型应用最为广泛［15］。本文利用正态云模型对可拓学的物元理论进行适当的改进。

正态云模型通过三元组（Ex，En，He）来表示。其中，期望值Ex表示该隶属云的中心位置，最能反映电力生产安全的划分等级；熵En是对其属性概念不确定程度的数学描述，有效地刻画了评估过程中分级边界的模糊性和随机性；超熵He是对熵的不确定性的度量，既体现了评估样本数据的离散程度，又客观描述了各评估因子模糊性与随机性之间的关联程度。通过以上三个数字特征来构造云隶属度函数，可解决电力生产安全等级界限值的模糊性和随机性问题，达到软化分级区间的目的。

2.2 可拓云模型

可拓学中的物元理论以物元作为描述事物的基本元，记为R=（N，c，v）。其中，N 是事物名称，c是事物特征，v是事物特征值。在传统的物元评估模型中，v常被视为定值，用来表示各项指标相应的等级，往往忽视了其本身的模糊性和随机性。本文考虑到云模型具有处理事物的双重不确定推理特性，利用正态云模型（Ex，En，He）取代v，从而实现对评估过程中随机性和模糊性的数学描述［16］。可拓云模型表示为

式中：R 为评估划分的等级；ci为评估指标；（Exi，Eni，Hei）为评估指标ci的云描述。

3 基于可拓云模型的电力生产安全综合评估方法

3.1 确定安全等级界限云模型

首先，将电力生产的安全等级划分为十分安全、安全、轻度危险、危险、十分危险5个等级，分别对应1～5级，用以标识电力生产安全水平。各评估指标的安全等级划分界限由统计分析和专家法综合得出，各评估指标的安全等级界限值［17］见表2。

表2 各评估指标的安全等级界限值Table 2 Grade limit of each evaluation index

其次，将评估各指标的安全等级界限当作1个双约束空间［cmin，cmax］来处理，兼顾约束空间的模糊性和随机性，适度扩展，并根据下式计算得出其相应正态云模型的3个数字特征［18］：

其中，He可结合相应指标的模糊性和随机性进行调整，本文取0.000 1或0.000 2。

最后，通过以上方法得到各评估指标的标准正态云模型，即各评估指标的安全等级界限云模型，详见表3。

3.2 可拓云模型的云关联度计算

根据电力生产安全综合评估的特点，将待评估的各项指标因子对应的值视为一个云滴，并随机生成服从对应期望值为Ex、标准差为He的正态分布的方差E′n，最终计算出各指标相应的待评估值x与安全等级界限云模型之间的云关联度k［19］。其计算公式为

通过式（9）可计算出待评样本数据与评估指标安全等级标准正态云之间的云关联度，并组成综合评判矩阵D：

式中：kij为评估指标ci与第j 级安全等级界限云模型之间的云关联度；n 为评估指标个数，本文取12；j为评判等级，本文取1～5的整数。

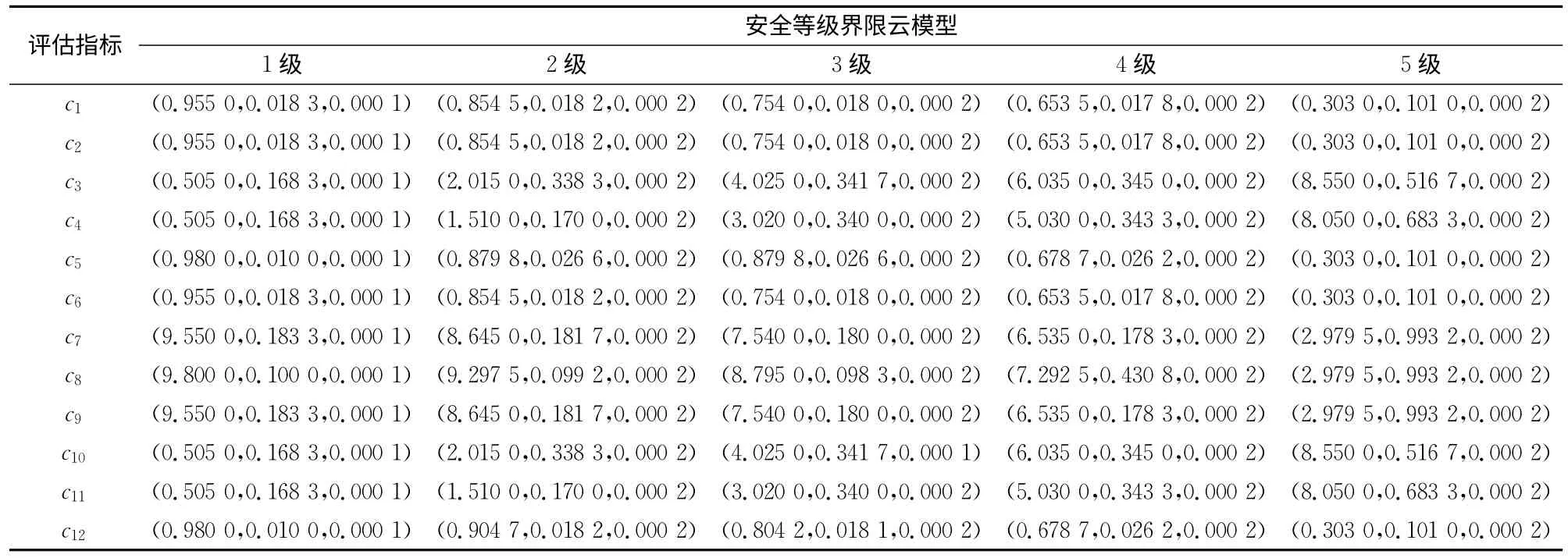
表3 各评估指标的安全等级界限云模型Table 3 Grade limit cloud of evaluation index

3.3 安全等级确定与危险识别

（1）计算综合评判向量G：

式中：W 为综合权重向量；D 为综合评判矩阵。

（2）计算评判的模糊等级特征值r：

式中：gi为向量G 对应的最大分量；fi为最大分量对应等级i的分值，本文中评判等级1～5对应的分数依次取值为1、2、3、4、5。

（3）多次计算求解，减少随机性

由式（9）可知，在求解云关联度k的过程中存在随机因素，因此需多次求解以尽量减少随机因素的影响。综合评判期望矩阵Dx、模糊等级特征期望值Erx、模糊等级特征熵值Ern分别为

式中：h为运算的次数，本文取200；D（i）为第i次计算得到的综合评判矩阵；ri（x）为第i次运算得到的模糊等级特征值。

（4）确定安全等级和可信信息

模糊等级特征期望值Erx最能反映电力生产安全综合水平，通过将其与1～5级的对应分值对比，可确定最终的安全等级。

模糊等级特征熵值Ern是评估结果离散程度的度量，其值越大，表示评估结果越分散。因此，本文引入置信度因子θ，用以标识评估结果的可信程度：其中，θ值越大，表示评估结果越分散，可信程度就越小；反之亦然［20］。

（5）危险识别

综合评判期望矩阵Dx反映了各个指标与5个安全等级间的关联程度，其第i个评估因子对应的最大云关联度maxjD（i）及其对应安全等级j代表该评估因子的危险程度，将低于2级的评估因子视为危险因素，并按其综合等级筛选危险因子。

假设其安全等级为m 级，则按危险程度取前m个评估因子作为危险因子，以实现对较危险因素的识别；若无危险因子，则危险因子为（null），表示安全且无较危险因素。

4 算例分析

4.1 算例简介

本文对某市电力公司的历史生产安全数据进行分析，通过统计和专家评分整理得到该公司2013年3～6月份4个月的各原始指标评估矩阵见表4。

表4 各指标原始评估矩阵Table 4 Original evaluation matrix

4.2 指标权重计算

首先利用层次分析法计算得到各指标主观权重向量Wa；其次基于历史生产安全数据，运用熵权法计算得到客观权重向量We；最后利用式（3）～（5）计算得到各指标综合权重向量W，其中a=0.611 9，b=0.388 1，其结果见表5。

表5 各评估指标的权重Table 5 Weight of each evaluation index for electric power production safety

4.3 评估结果及对比分析

首先通过式（9）计算各指标的云关联度；再通过式（11）～（16）计算确定安全等级及其对应的置信度因子θ 和危险因子；最终将以上评估结果与文献［4］、［8］的评估结果进行对比分析，见表6。

表6 评估结果对比Table 6 Comparison of the evaluation results

由表6可知，本文评估结果与文献［4］、［8］得到的评估结果基本一致，从而验证了本文提出的评估方法的有效性和合理性。但值得注意的是，本文所提出的评估方法在得出电力生产安全综合评估等级的同时，还给出了评估结果的置性度因子和危险因子。其中，本算例的置信度因子θ均小于0.01，表明评估结果较为可信；危险因子列出了电力企业生产过程中的较危险因素，为电力企业整改提供了方向。

5 结论

（1）本文综合了云模型和物元理论的优点，提出了用可拓云模型来评估电力生产安全综合状态，有效地解决了分级边界的模糊性和随机性，在得到评估结果的同时给出了置信度因子和危险因子，明确了评估结果的可信程度和整改方向，为电力生产安全综合评估提供了一种新思路。

（2）通过算例分析验证了该方法具有较高的可行性和合理性，同时对提高电力生产安全综合评估的准确度具有一定的工程应用价值。

［1］姚建刚，肖辉耀，章建，等.电力安全评估与管理［M］.北京：中国电力出版社，2009：14-28.

［2］施泉生，詹必雄.模糊决策方法在电厂企业安全评价中的应用［J］.华东电力，2003，31（12）：11-13.

［3］胡翔.灰色关联度评价法在电网安全性评价中的应用［J］.华东电力，2009，37（6）：1029-1032.

［4］胡涛，黄健，鄢威.一种电力生产安全性评价方法研究及应用［J］.电力系统保护与控制，2009，37（16）：46-49.

［5］周姝.电力生产班组安全管理能力成熟度模型研究［J］.中国安全生产科学技术，2012，8（4）：161-165.

［6］焦晓佑，胡兆光，宋守信，等.智能化的电力安全文化评估模型与仿真［J］.北京交通大学学报，2008，32（2）：48-52.

［7］孙志禹，周剑岚.一种基于行为因素的高危作业安全评价方法的研究［J］.水力发电学报，2011，30（3）：195-200.

［8］马丽云，施泉生.基于云重心理论的供电企业安全评价方法［J］.华东电力，2011，39（8）：1370-1373.

［9］张鹄志，马传明，王江思.基于层次分析-熵权法的中原城市群生态环境评价［J］.安全与环境工程，2014，21（1）：87-92.

［10］肖辉耀，姚建刚，章建，等.电网安全评估体系分析［J］.电网技术，2009，33（12）：77-82.

［11］王莉霞，滑帅，梁金燕，等.基于BP神经网络的电网调度系统安全评价［J］.安全与环境工程，2013，20（6）：126-129.

［12］庄万玉，凌丹，赵瑾，等.关于敏捷性评价指标权重的研究［J］.电子科技大学学报，2006，35（6）：985-988.

［13］叶军，陈学嘉.组合权重法在建筑施工企业安全评价中的应用［J］.安全与环境工程，2013，20（6）：130-136.

［14］Li D Y.Uncertainty reasoning based on cloud models in controllers journal of computer science and mathematics with application［J］.Elsevier Science，1998，35（3）：99-123.

［15］李德毅，刘常昱.论正态云模型的普适性［J］.中国工程科学，2004，6（8）：28-34.

［16］胡涛，王树宗，杨建军.基于云模型的物元综合评估方法［J］.海军工程大学学报，2006，18（1）：85-88.

［17］李如琦，苏浩益.基于可拓云理论的电能质量综合评估模型［J］.电力系统自动化，2012，36（1）：66-70.

［18］王威，侯本伟，苏经宇，等.基于云化物元模型的供水管网抗震服务功能评价［J］.北京工业大学学报，2013，39（7）：994-1001.

［19］谢庆，彭澎，唐山，等.基于云物元分析原理的电力变压器故障诊断方法究［J］.高压电器，2009，45（6）：74-77.

［20］李玲玲，朱芬芬，姚致清，等.基于可信度的可靠性度量云模型［J］.电力系统保护与控制，2012，40（8）：90-94.