研究生数学建模的特点与培训策略研究
2015-12-04贾利新张小勇
贾利新 张小勇
摘要:数学建模就是用数学语言描述实际现象的一个过程。是一种数学的思考方法,是运用数学的语言和方法,通过抽象、假设、简化建立能近似刻画并解决实际问题的一种强有力的数学手段。本文结合教学实践,结合建模的特点,对数学建模的课程的教学改革提出几点建议。
关键词:数学建模;数学语言;教学改革
中图分类号:G643 文献标志码:A 文章编号:1674-9324(2015)18-0205-02
全国研究生数学建模竞赛是针对当前全国在读研究生的竞赛活动,主要是激发研究生对生活实际的创新同时提高研究生的学习兴趣,提高学生对于与数学模型的建立和通过运用计算机对实际问题进行解决的综合能力,拓展学生的知识面,培养大家的团队合作意识和对事物的创新精神,从而使优秀的学生能够在过程中通过实践脱颖而出,迅速地成长起来。推动研究生教育改革,能够更好地增进学校与学校之间的友谊关系。从2004年起开始举办以来,我校参加了历次竞赛,均取得了优秀的成绩,这项竞赛在我校研究生中的影响力越来越大,在广大研究生中也打下了扎实基础。该活动已经成为我校一项重要的课外活动之一,也成为研究生培养阶段的一个重要实践环节。
一、数学建模的概念
数学建模是利用数学方法解决实际问题的一种实践方式。通过抽象、简化、假设、引进变量等途径将实际问题用数学的方式表达出来。建立数学模型,运用数学方法和先进的计算机技术对实际问题进行解答。
二、研究生数学建模的特点
我国的大学生数学建模竞赛是从1992年开始的,分析20多年来的赛题可以发现,这些赛题虽然来自于实际问题,但这些问题经过命题人和全国组委会的研讨和加工后,距离真正的数学问题已经很接近了,需要学生事先做的假设并不是很多。由于大多数命题人都是数学老师,尽管赛题具有一定的实际背景,但赛题本身所包含的专业知识不是很多,对于本科生而言,读懂赛题需要的时间并不是很多。例如1998年的投资的收益和风险问题,学生不需要专门的经济学知识,就能够很轻松地完成试题;2011年的交巡警服务平台的设置与调度问题,学生不需要专门的交通管理知识,只要有日常的交通规范常识就可以完成,在加上赛题所需的数据命题人也都给出了,这就大大减轻了学生收集数据的负担。从完成赛题所需的数学知识来看,传统的高等数学、线性代数、概率论与数理统计基本是够用的,当然有些时候还要加上一些最简单的运筹学和图论知识等。
相比之下,研究生数学建模竞赛的赛题更为开放。其题目一般来自工程技术和管理科学等方面的实际问题,虽然也不要求参赛者预先掌握深入的专门知识,但由于命题人大多都是课外人员,这就造成了出题的不严谨,造成好多的题目专业性较差,甚至有的题目还是命题人的科研项目里尚未解决的问题,因此这就造成了许多题目数学味道比较“淡”,学生在答题过程中有些专业知识用不上,经过作者十年来的实践发现,很多研究生觉得由于不是专业性人员出题,造成题目脱离常规的学习项目,出题的范围过深,题目“晦涩难懂”,为了能够读懂题目就需要花费一定的时间去查证研究,由于题目中涉及到一些专业术语,这就要求研究生拿出一定的时间查阅相关的专著和网上资源,浪费了很多的时间和精力。例如2007年的机械臂运动路径设计问题,就需要学生对机械设计问题要有初步的了解才能够读懂并解答,2011年的基于光的波粒二象性一种猜想的数学仿真问题,需要学生掌握的物理学知识是比较多的,从而在回答问题过程中,不仅仅是有数学知识,还需要大量的物理知识,因此我们在教学过程中也要适当地去适应这种出题的模式,否则学生在今后回答问题的时候会有有力无处使的感觉。
从以上例题不难看出,历年的赛题都是从实际问题出发,而好多的赛题都脱离了数学的范围,要想更好地解决问题,常规的解决方法不但需要大量的数学知识同时还需要很多的其他方面的知识,而数学建模的利用不但能够快速地解决实际问题,还能够为学生节省很多的时间和精力。数学建模从概念上来看就能够看出,这是一种独特的解决实际问题的方法,它是将实际问题通过各种方法将实际问题多元化并结合计算机离散数学的运用以数学的方式解决出来。这种方法的运用更能够让实际问题快速地得到解决。而离散数学其独特的离散性,也是从多个方面去解决问题,因此数学建模与离散数学的相结合是为解决实际问题量身定做的模式。针对这种方法如果我们把它运用到实际问题中,在解决起来就容易多了。只要将问题通过运用抽象、简化、假设、引进变量等方法去多元化,通过离散数学的特性,将几种或者多种元素进行分析,从而使问题的结果轻松就计算出来,在很大的程度上解决了因多方知识点不足而不能解决的问题,这就是数学建模的特点,运用一定的方法,通过多元素分析,从而轻松地解决实际生活中所遇到的问题。
三、研究生数学建模培训的培训策略
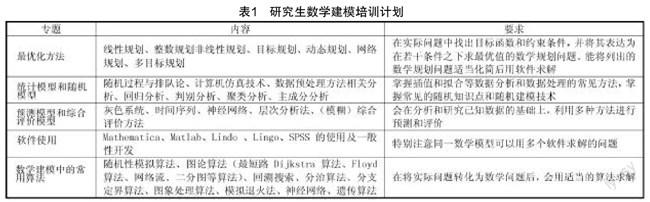
鉴于研究生数学建模的上述特点,我们在建模培训时,不再对传统的高等数学、线性代数、概率论与数理统计中的基本知识进行专门讲解,按照数学建模所需数学知识,分专题进行培训,重点讲授图论、运筹学、多元统计分析、模糊数学的内容及其在建模中的应用,具体计划如下。
通过多元化强化的学习与实践,能够让学生更快地将生活实践与学习的理论结合起来,在真正地解决起问题来更快捷方便。通过分专题进行培训,让学生的各知识点记忆得更加牢固,运用起來更能得心应手。问题解决方便了,那么对于促进国家的发展也能起来良好的作用。
与此同时我们还鼓励研究生挖掘所学专业中的一些数学模型进行交流,这样做的目的就是将数学模型与专业学习相结合,使学生能够从切身感受与专业融合在一起,从而为将来在实践中能够灵活地穿插运用,将数学模型作为专业学习的一部分。研究生数学建模竞赛的培训得到了导师们的大力支持,一些研究生导师还为我们们提供了许多相关领域的数学模型供我们在培训过程参考。导师们普遍反映,经过数学建模训练后,学生们的数学意识提高了,会“戴着数学眼睛”来进行专业学习,会进行“定量化”思维,写出的学术论文更加规范了。一位导师甚至谈到,无论博士论文还是硕士论文,无论理科论文还是文科论文,如果没用一些数据作支撑,如果没有使用一些数学方法来进行分析,文章通篇都是文字叙述,那么这样的论文是不成功的。作者多年的实践表明,数学建模的思想实际上已经融入了研究生学习的整个过程,成为研究生培养的一个重要工具和途径。
因此在对学生培训的时候,一定要针对数学建模的特点,让学生能够更多元化地去建立数学模型,在将来实际生活中遇到问题也能够有更多的方法和手段去处理所遇到的问题。单点多元化的培训,能够让学生对知识掌握得更牢靠,同时在运用过程中也能够将问题同时多元化地去分析,通过运用数学的思考方式,使问题迎刃而解。所以改变大面灌的局面,使学生从各个学习的要点单点去突破,建立更多的数学模型,更容易让学生能够创新出好的思路和模式,为研究新课题开创出新的局面。这也是数学建模特点的灵活运用,所以我们在今后的培训过程中一定要改变过去的死板模式,充分发挥学生们的积极性,开发学生们对于学习和创新的潜力,从而能够真正地达到学习与实践融合一体的目的。分析数学建模的特点,依据竞赛问题的内容,结合实际问题的解决结果,充分将数学建模运用到生活当中去。
参考文献:
[1]刘来福,曾文艺.数学模型与数学建模[M].北京:北京师范大学出版社,1997.
[2]刘保东等.数学建模与数学实验[M].北京:人民邮电出版社,2008.
[3]韩中庚,宋明武,邵广纪.数学建模竞赛——获奖论文精选与点评[M].北京:科学出版社,2007.
