非奇异M-矩阵Hadamard积的最小特征值的改进估计式
2015-12-04周平文山学院数学学院云南文山663000
周平 (文山学院数学学院,云南 文山663000)
1 基本概念和引理
令N={1,2,…,n},Cn×n(Rn×n)表示所有n×n阶复(实)矩阵构成的集合。
定义1[1~9]设A=(aij)∈Rn×n,若aij≥0;i,j∈N,则称A为非负矩阵,记为A≥0;若aij>0;i,j∈N,则称A为正矩阵,记为A>0。
定义2[1~9]记Zn×n={A=(aij)∈Rn×n|aij≤0;i,j∈N;i≠j},称Zn×n中的矩阵A为Z-矩阵,简记A∈Zn×n。
定义3[1]设σ(A)={λi=1,2,…,n}(λi是A的所有特征值),则σ(A)叫做A的谱;矩阵A的n个特征值的模的最大者称为A的谱半径,记为ρ(A),即ρ(A)=max{|λi|,i∈N}。
定义4[1]若A=(aij)∈Zn×n可表示为A=sI-P,其中P≥0,s≥ρ(P),则称A为M-矩阵。
特别地,当s=ρ(P)时,称A为奇异M-矩阵;当s>ρ(P)时,称A为非奇异M-矩阵。记所有n×n阶非奇异M-矩阵所成之集为Mn。
引理1[1]设A∈Zn,则A∈Mn当且仅当A-1≥0。
引理2[1]设A≥0,若A的谱半径ρ(A)是A的一个特征值,即ρ(A)∈σ(A),此时称ρ(A)为A的Perron特征值。
定义5[1]设A=(aij)∈Zn×n,记τ(A)=min {Re(λ)∈σ(A)},称τ(A)为A的最小特征值。
引理3[2]若A∈Mn,则τ(A)为A的模的最小特征值,且τ(A)=>0。
定义6[1~9]设A=(aij)∈Cm×n,B=(bij)∈Cm×n,用A◦B表示A和B的对应元素相乘而成的m×n阵,即:

称其为A和B的Hadamard积,也称为Schur积。
引理4[2]设A,B∈Rn×n都为M-矩阵且B非奇异,则A◦B-1为M-矩阵。
引理5[1]若A是M-矩阵,则存在正对角矩阵D,使得D-1AD是行严格对角占优M-矩阵。
引理6[1]设A,B∈Rn×n,且D,E∈Rn×n是对角矩阵,则:

引理7[1]设A∈Mn,D=diag(d1,d2,…,dn),di>0(i=1,2,…,n),则D-1AD是M-矩阵。
引理8[6]若A=(aij)∈Cn×n,则对任意的0≤α≤1和任意的正实数组x1,x2,…,xn,A的特征值位于下列区域:

设A=(aij)∈Rn×n是非奇异M-矩阵,对任意i,j,k∈N;i≠j,定义:

引理9[9]如果A=(aij)∈Rn×n是一个行严格对角占优M-矩阵,则A-1=(βij)存在,且:

引理10[9]如果A=(aij)∈Mn是一个行严格对角占优M-矩阵,则A-1=(βij)存在,且:

引理11[9]如果A=(aij)∈Rn×n是M- 矩阵,A-1=(βij)是双随机矩阵,则:

2 主要结论
定理1 设A=(aij)∈Mn,B=(bij)∈Mn,A-1=(βij),则:

证明 因为A∈Mn,所以应用引理4~引理7,存在正对角矩阵D,使得D-1AD是严格对角占优M- 矩阵,且有τ(B◦A-1)=τ(D-1(B◦A-1)D)=τ(B◦(D-1AD)-1)。为了不失一般性,假设A是严格行对角占优M-矩阵。
(Ⅰ)如果矩阵A和B都是不可约矩阵,令=ajk|mki;i,j∈N;j≠i,则:

因此,存在实数εji(0≤εji≤1),使得:

从而:

又令εj=,则0<εj≤1(如果εj=0,则A是可约矩阵,这与假设矛盾),所以:

因为A是不可约矩阵,所以:

记τ(B◦A-1)=λ,则根据引理8和引理9知,存在i(1≤i≤n),有:

即:
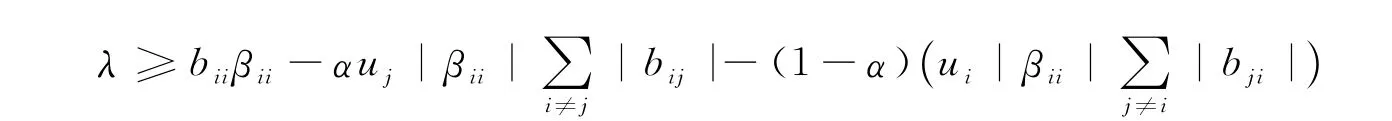
由引理3,上式可变为:

故:
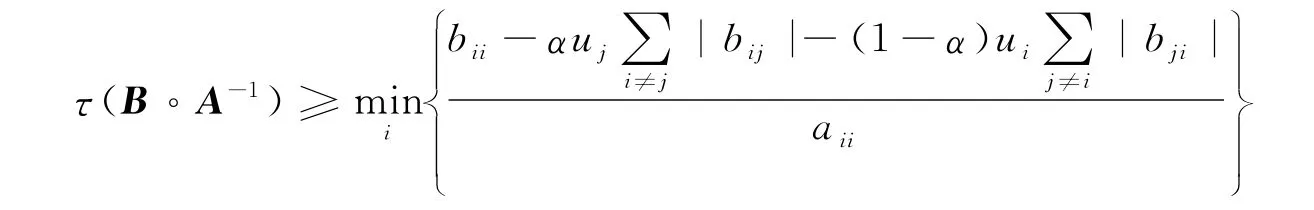
(Π)如果A和B中至少有一个是可约矩阵时,令:

由于A,B∈Mn,从而对任意正数δ,只要δ足够小时,A-δT与B-δT的所有主子式为正,且A-δT,B-δT是不可约的非奇异M-矩阵[3],用A-δT和B-δT分别替换A,B,并且令δ→0,由(Ⅰ)和连续性可得该结论。
注1 在定理1中,当α=0时,得到:

即为文献[9]中的定理3.4。
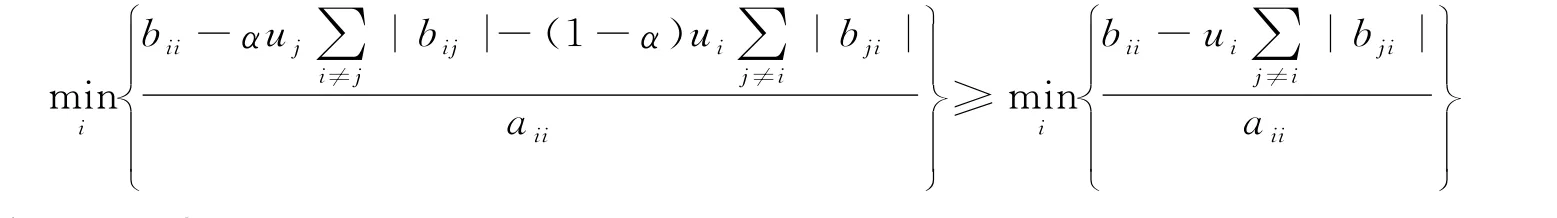
事实上,因为:

所以:

定理2 若A=(aij)∈Rn×n是严格行对角占优M-矩阵,A-1=(βij),则:

证明 类似于定理1的证明,只须将定理1的证明过程中的bij替换成aij,bii替换成aii,便可得到定理2的结果。
定理3 设A=(aij)∈Mn,B=(bij)∈Mn,且A-1=(βij)是双随机矩阵,则:

类似定理1的证明即可得到以上结论。
定理4 设A=(aij)∈Mn,A-1=(βij)是双随机矩阵,则:

证明 在定理3中令B=A即可得到该定理。
注3 在定理3和定理4中,当α=0时,分别得到:

即为Cheng Guanghui等[9]给出的定理3.1。

根据注1、注2、注3和注4可知,笔者所给出的这些估计式在一定条件下改进了已有文献的结果。
3 算例分析
例1 令:

显然A,B∈Mn。
应用 Matlab7.0计算τ(B◦A-1)=0.2148;
应用文献[2]中定理5.7.31的估计式,得τ(B◦A-1)≥0.07;
应用文献[7]中定理9的估计式,得τ(B◦A-1)≥0.052;
应用文献[8]中定理2.1中的估计式,得τ(B◦A-1)≥0.075;
但应用定理1,取α=时,得τ(B◦A-1)≥0.1742。
在这里,A是双随机矩阵,应用 Matlab7.0计算τ(B◦A-1)=0.9755。
应用Fiedler和 Markham的猜想得τ(A◦A-1)≥0.05;应用文献[7]中定理3.1得τ(A◦A-1)≥0.06624;应用文献[8]中定理3.2得τ(A◦A-1)≥0.7999;应用文献[9]中定理3.1得τ(A◦A-1)≥0.8250。但应用定理4,取α=时,得τ(A◦A-1)≥0.9211。
对该算例的计算结果作比较可知,笔者给出的新估计式改进了Fiedler和Markham的猜想以及现有文献的结果,所得结论是对相关文献的一个有益补充。
[1]陈公宁 .矩阵理论与应用 [M].北京:科学出版社,2007.
[2]Horn R A,Johnson C R.Topic in Matrix Analysis [M].New York:Cambridge University Press,1991.
[3]Fiedler M,Markham T.An inequality for the Hadamard Product of anM-matrix and InverseM-matrix [J].Linear Algebra and its applications,1988,101:1~8.
[4]Yong X R.Proof of a conjecture of Fiedler and Markham [J].Linear Algebra and its applications,2000,320:167~171.
[5]Huang R.Some inequalities for the Hadamard product and the Fan product of matrices [J].Linear Algebra and its applications,2008,428:1551~1559.
[6]Cvetkovic L.H-matrix theory vs.eigenvalue localization [J].Numer Algor,2006,42:229~245.
[7]Li H B,Huang T Z,Shen S Q,et al.Lower bounds for the minimum eigenvalue of an M-matrix and its inverse [J].Linear Algebra and its applications,2007,420:235~247.
[8]Li Y T,Chen F B.Wang D F.New lower bounds on eigenvalue of the Hadamard product of an matrix and inverse [J].Linear Algebra and its applications,2009,430:1423~1431.
[9]Cheng G H,Tan Q,Wang Z D.Some inequalities for the minimun eigenvalue of of the Hadamard productof an matrix and inverse [J].Linear and Multilinear Algebra,2013,65:1029~1038 .
