基于混沌理论与小波包分析的舰船状态监测方法

郑 勇，贾丙辉，李光荣

(南京工程学院 机械工程学院，江苏 南京211167)

0 引 言

随着经济发展，通过舰船进行货物运输越来越频繁，保证舰船的安全性，快速准确的检测到舰船的状态并对舰船的故障进行排除具有非常重要的现实意义。船舶的故障诊断是在复杂并且多种不确定性并存的环境下进行，目前对于舰船状态监测的方法有很多，比如主元分析法、时域分析法等，但是并没有达到实时性，并且精度不够。

本文鉴于小波包能够将很多频带信号有效的分析出来，并且能很好的去除信号中噪声的特点［1-2］，以及混沌理论的非线性、非平衡和抗干扰性强的特点，将二者相结合进行舰船状态监测。首先利用小波包分析分解可能引起舰船状态发生变化的特征信号，然后利用混沌理论对信号进行特征提取，确定是哪个部位发生故障，最后通过实验进行验证本文所设计算法的可靠性。

1 小波包分析

小波包分析解决了信号分解时在高频部分频域分辨率低，低频部分时域分辨率低的问题。小波包分析通过分解将信号分解为高频部分和低频部分，然后对高频部分进一步分解，将分解信号的特征与相应的频带进行匹配，同时提高了频域和时域的分辨率。

小波变换的尺度表达式为:

式中g(n)=(-1)1-nh(1- n)。

令φ0(x)=φ(x)，φ1(x)=ψ(x)，则式(1)为:

对于函数φn，在n=2l(偶数)或者n=2l+1(奇数)时，正交尺度φ(x)的小波包表达式为:

通过式(4)描述小波包的空间分解:

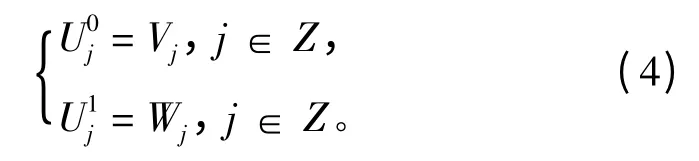
所以正交分解Vj+1=Vj⊕Wj可以用表示，即:

同时可以扩展到n 为非负整数时，

对于2j大小的信号f(x)在空间中形成的J 层小波包分解如下:

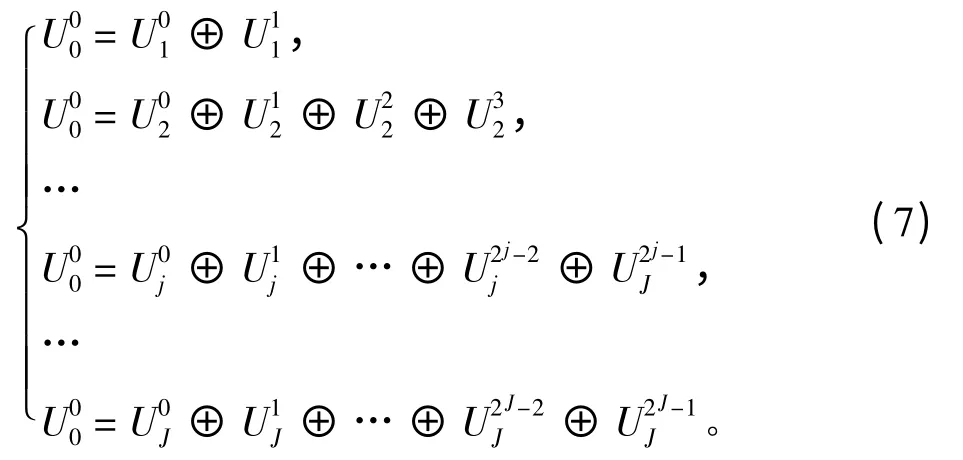
从上式可知:信号可以被分解为J 层，在第j 层信号空间包含2j个正交子空间，每个子空间对应一个分解的节点，所以整个分解过程共形成2j+1-1个节点，其分解示意图如图1所示。

图1 小波包分解示意图Fig.1 Wavelet packet decomposition schematic

2 混沌理论

1)混沌系统

令连续映射f:I →I ⊂R，若存在无穷集合S ⊂I以及符合以下条件则称f 在S 上混沌:

①S 中没有迭代的点;

②对于任意的x1，x2∈S(x1≠x2)得:

f′(·)=f(f…(…f(·)…))含有t 重;

③对于任何的x1∈S和f 上的一点P ∈I 则:

2)混沌性判别

混沌系统是非线性的，但并不是所有的非线性系统都是混沌的，所以利用混沌理论进行混沌特征提取时，必须判断系统是否在混沌状态下。本文利用Lyapunov 指数［3］进行混沌性判别。

图2 Lyapunov 指数定义示意图Fig.2 Lyapunov index schematic definition

根据图2，xn+1=f(xn)时，

当ε →0，N →∞时，则可以求出

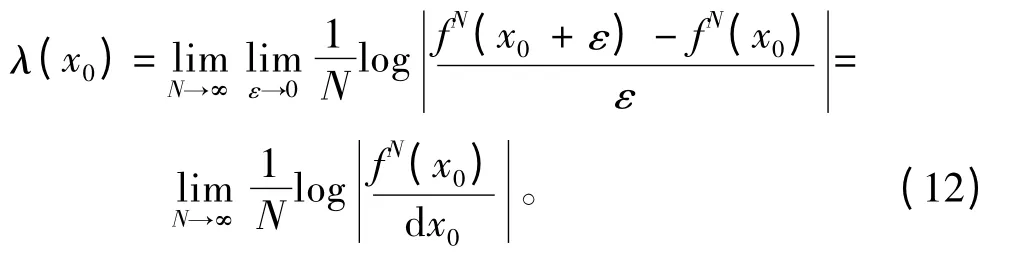
说明eλ(x0)是最近邻点在一个周期后所循环出现距离的平均因子。所以由式(12)和链条法则知［4］:

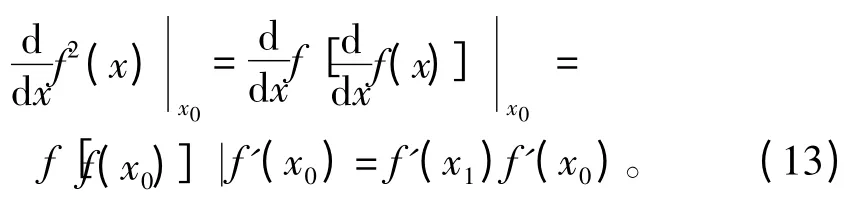
从而得到Lyapunov 指数:

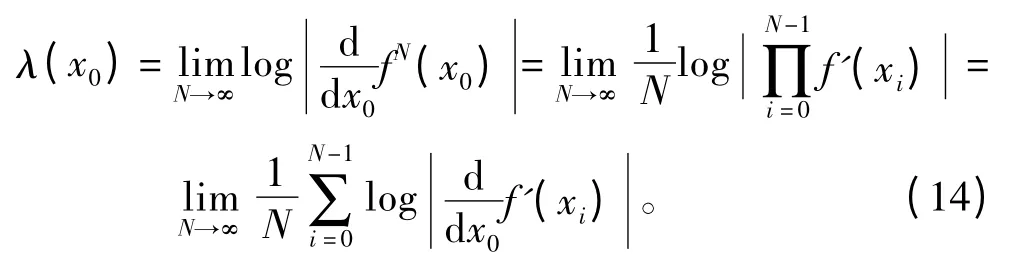
同时将λ(x0)作为λ。在λ < 0 时，舰船对干扰、故障等因素不敏感，相对空间逐渐变小，才是系统稳定;在λ=0 时，系统处于稳定与不稳定的临界点;在λ > 0 时，干扰等外界条件以指数倍数被放大，系统在局部空间中表现为不稳定的状态，此时可以认为系统混沌状态。

3)分形维数

本文用分维数来描述舰船故障特征向量，实现对系统故障诊断［5］。在众多分形维数中关联维数是非常典型的一种方法，定义为:

式中:C(r，m)表示积分。描述为:

式中:N(m)为嵌入维个数是m 时，小波包分解重构向量的数目。H(·)描述为:

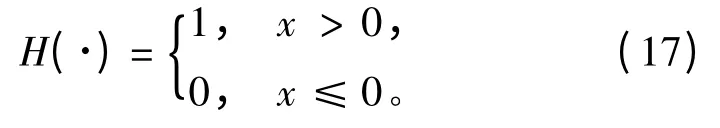
在求关联维数时，考虑到长度的有限性，所以维数的上限为:

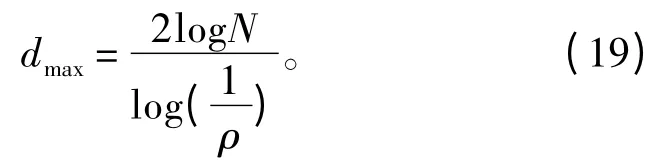
对于小波包重构得到的时间序列为x1，x2，x3，…，xn(n=1，2，…)，重构空间为B:

空间中向量的距离为:

在最大距离和最小距离之间取一个合适的值r，求得距离小于r的向量所占的比重:

从而得到关联维数:

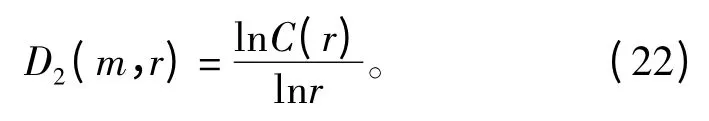
取值时r 太大有用信号被掩盖，太小会使干扰信号增强，所以r的取值是通过lnC(r)- lnr 曲线，找到曲线中非常接近直线部分对应的r 作为所要选取的范围。

充分利用系统初始状态和相空间轨道的多少对混沌的影响来研究系统故障时吸引子的动态变化，从而实现对舰船状态的检测和故障的诊断。

3 基于混沌理论和小波包分析的舰船状态监测实验结果

设置输入转速为2 100 r/min，所加负载为260 N·m，进行4个循环，第5 次时3 档齿轮出现断裂，系统发生故障，通过上文的分析，计算二、三档时齿轮故障时的信号关联维和K 熵，进行仿真实验。

由表1和表2 可知:二档时关联维数在0.157 5左右变化不明显，而三档时关联维数在第5 次循环时突然从0.179 1 变为了0.243 1，说明三档可能出现故障，同时从K 熵也可以看出，二档时K 熵在1.033 5 左右变化不明显，而三档时K 熵在第4 次循环时突然从1.243 3 变为了1.243 7。从而说明在二档时舰船正常运转，三档时第7个周期发生故障。

表1 二、三档时齿轮故障时的信号关联维Tab.1 Kdimension of second gear and third gear when failure

表2 二、三档时齿轮故障时的信号K 熵Tab.2 Signal correlation dimension of second gear and third gear when failure

4 结 语

本文从对混沌理论和小波包的分析中获取了各自特点，并且将二者相结合进行舰船状态的检测，首先利用小波包分析分解可能引起舰船状态发生变化的特征信号，然后利用混沌理论对信号进行特征提取，确定是哪个部位发生故障，最后通过实验进行验证本文所设计的算法的可靠性。

［1］崔金泰.小波分析导论［M］.西安:西安交通大学出版社，1997:328-335.

［2］杨国安.机械故障信号小波包分解的时域特征提取方法研究［J］.振动与冲击，2001，20(2):25-28.YANG Guo-an.Research domain feature extractionmethod of mechanical fault signal wavelet packet decomposition［J］.Journal of Vibration and Shock，2001，20(2):25-28.

［3］敖力布，林鸿溢.分形学导论［M］.呼和浩特:内蒙古人民出版社，1996.

［4］梁世清，王德明，刘维亭.基于Lyapunov 指数的舰船电力系统稳定性分析［J］.舰船科学技术，2008，30(1):76-79.LIANG Shi-qing，WANG De-ming，LIU Wei-ting.Stability analysis in ship electrical power system based on Lyapunov exponents［J］.Ship Science and Technology，2008，30(1):76-79.

［5］黄润生.混沌及其应用［M］.武汉:武汉大学出版社，2000.