破冰船阻力性能预报方法综述

王 超，孙文林，康 瑞，王国亮

(哈尔滨工程大学 船舶工程学院，黑龙江 哈尔滨150001)

0 引 言

破冰船的阻力问题作为破冰船设计过程中的关键问题之一，对于破冰船的设计有着决定性的影响。虽然国外学者已经对其有了深入的研究，在国内却尚属起步阶段，为此，本文将就实船试验、模型试验、经验或半经验公式以及理论预报等几种破冰船阻力研究的主要方法进行系统地阐述和分析。

1 实船试验

早期的破冰船阻力研究主要是在实船试验的基础上对试验结果加以分析。时至今日，虽然模型试验技术已经比较成熟，结果也比较可靠，却仍然难以完全模拟自然条件下的破冰过程。所以，在破冰船的阻力研究中，实船试验不可取代。

实船试验前要进行环境条件的观测、船舶参数的观测和船舶状态的观测三方面工作。为了评估破冰船的阻力性能，通常选择推力一定时在某一冰层厚度下的航速来进行试验。试验区域一般会选择冰层厚度尽可能均匀的地点，以保证试验尽可能接近于船舶在平整冰中的航行状态，如图1所示。

图1 破冰船实船试验Fig.1 Full scale test of icebreaker

破冰船的实船试验过程与常规船舶类似，但为了研究海冰对船舶航行性能的影响，需要对海冰的相关参数及有关的气象数据进行详细记录。

实际工作中冰的强度常用弯曲强度来衡量，但由于测量工作耗时耗力，因此多直接运用公式或图谱由盐度和温度等参数得出，如Timco和O＇Brien［1］建议的海冰抗弯强度计算公式为:

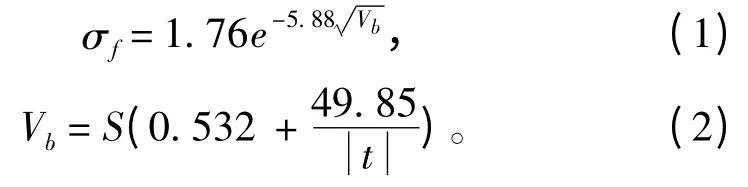
式中:S 为海水盐度;t 为海水温度;Vb为盐水体积。

传统航道和冰脊的档案通常由钻探获得，但随着遥感卫星的普及和应用，如今的冰情档案多是通过卫星数据得到，遥感卫星获得的图像如图2所示。

为了实时测得冰层的厚度，试验时还会用到特殊的电磁探测系统(见图3和图4)。该系统会向海水发出一个电磁场。由于冰的导电率相对于海水而言很低，因此可以忽略冰的导电率，通过测量电磁场强度得出设备距离海面的距离。再使用1 台声波测高仪或激光测高仪测出设备距离冰面的高度，就可以将两者测得的距离相减获得冰层的厚度。

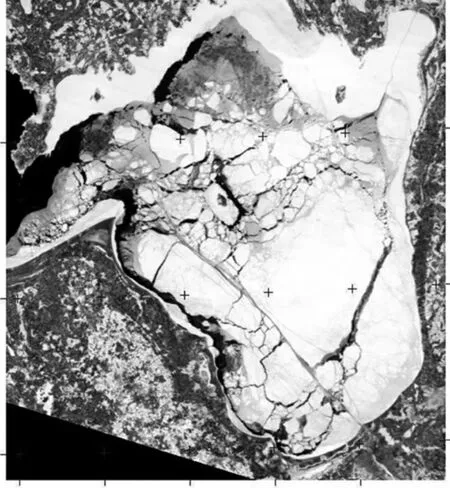
图2 遥感卫星可视波长图像中的冰层Fig.2 Ice sheet inmODIS visual length image

图3 首部的冰层厚度电磁探测装置Fig.3 Electromagnetic system on the bow

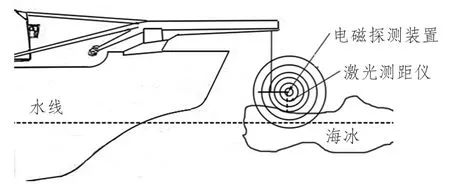
图4 冰厚测量装置示意图Fig.4 Sketch of ice thickness measuring system

实船试验虽然在冰阻力值的测量和冰层破坏模式的观测上有着不可取代的作用，但是试验成本很高。因此，随着模型试验技术的发展，大量的试验工作都已经改为采用模型试验的方式进行。

2 模型试验

随着1955年在列宁格勒建立起世界上的第一座冰池，冰池模型试验技术开始进入人们的视线。到20 世纪70年代人们开始重视模型试验，并陆续在各地开始了冰池的建造［2］。

相比于实船试验，模型试验有准备时间短、花费低的优势。随着冰池试验技术的提高和试验设备的改进，目前的冰池试验结果已经能够满足一般科研和设计工作的需要。图5 为HSVA的冰池结构图。

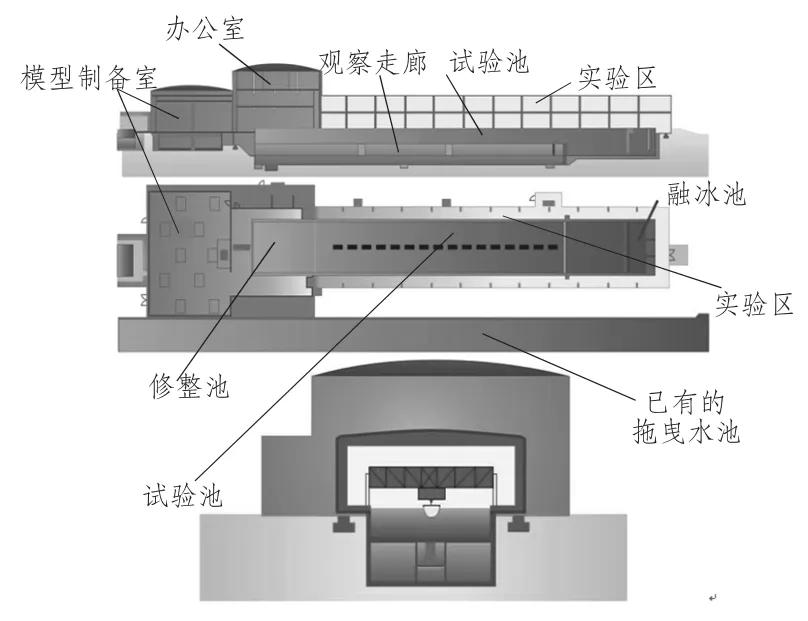
图5 HSVA 冰池结构图Fig.5 Structure drawings of HSVA＇s ice tank

冰池试验过程中，由于涉及到海冰与船体间的相互作用，需要对海冰进行模拟并保证模型冰符合相似性准则的要求，其试验参数的相似性关系如表1所示。

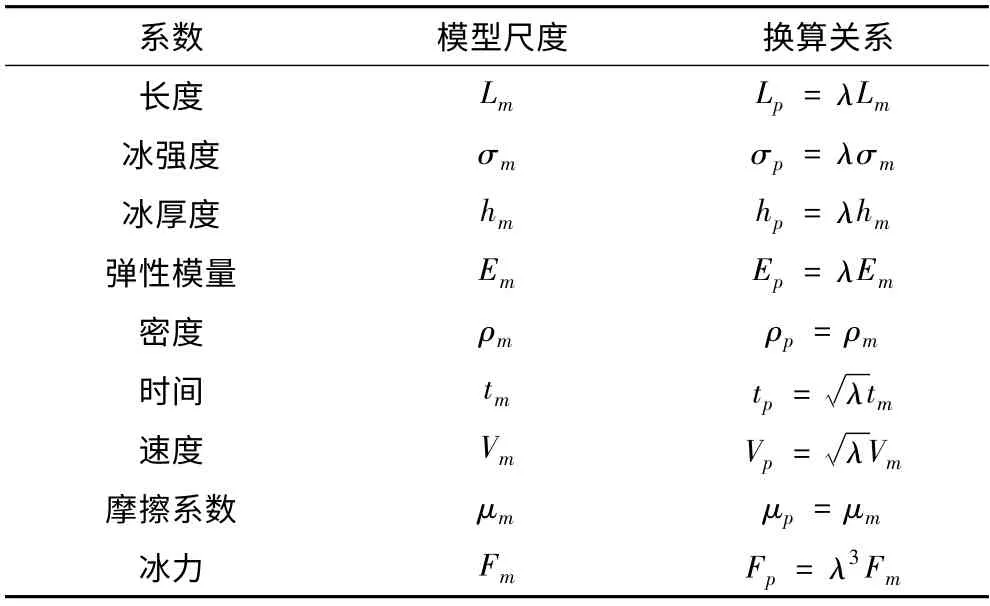
表1 冰池试验相似性关系表Tab.1 Similarity relationship of ice tank test

早期的冰池试验大多只考虑到傅汝德相似准则。直至1980年，Timco［3］指出柯西相似准则的满足与否影响着模型冰的破坏形式、船体的纵摇运动和冰层的破碎与浸没，所以适当的柯西数对于实验结果的可靠性有着重要的影响。试验中海冰弹性模量(E )与强度极限(σ)的比值如果与实尺度数据保持一致，根据柯西相似准则可以得到式(3):

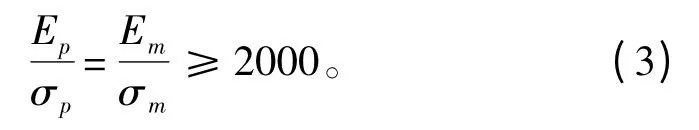
模型试验对于相似性的严格要求使模型冰制备的好坏成为试验结果准确与否的一项重要影响因素。已有的模型冰可以分为低温冻结模型冰和非冻结模型冰两大类［4］。二者的区别就在于是否需要采用降温过程来进行模型冰的制备。目前各地冰池中得到广泛采用的是低温冻结模型冰。这是因为低温冻结模型冰不仅可以较好地满足试验对模型冰强度的要求，使用了氯化钠溶液或其他溶液冻结而成的模型冰往往可以更好地还原海冰的内部晶体结构，得到的测量结果也更为准确。

最早得到应用的模型冰是盐水冰，但是盐水冰的使用受限于抗弯强度而无法满足大多数冰池对于缩尺比的要求。1979年Timco［5］提出了尿素模型冰的制备方法。作者在对多种掺合物进行研究、比较后提出了尿素的水溶液制成的冻结模型冰并被各地的冰池所广泛采用。

自然条件下的海冰随着厚度的增加，晶体成长的方向会由随机分布变为一致的垂向生长，使海冰下部区域的强度大为下降。实际工作中会利用这一特点，在室温达到冰点以下后向冰池上空喷水，使液滴在空中凝结形成冰晶。这些冰晶会落到水面上成为晶核，加快模型冰的冻结;促使冰晶的垂向生长，使其强度降低;同时，减小晶体的直径，防止因晶体直径过大而造成冰层破坏形式的改变［6］。

由于冰层强度随温度升高而降低，制冰时也会在冰层的厚度达到目标厚度前关闭冰池的制冷系统，使整个冰池的温度升高到冰点附近，从而达到降低冰层强度的目的。

随着模型冰制作技术的发展，这些年也出现了一些新型的模型冰。如1986年Timco［7］制作出了新型的EG/AD/S 模型冰。EG/AD/S 即乙二醇、脂肪族洗涤剂和白糖。但是这种模型冰因为含有糖分，会导致细菌繁殖，使冰池难于维护。而且EG/AD/S冰制备成本高，因此没有得到普及。

国内的模型冰研究方面大连理工大学于2000年制成了采用聚丙烯粉、水泥、塑料微珠等成分的DUT-1 型非冻结模型冰，并通过实验证实该模型冰的物理和力学指标已能较好地满足实验的要求［4］。

另外，试验相似性要求实船与试验条件下船体与海冰间的摩擦系数相等。为此，船模的表面需要喷涂特制的涂料，并于试验前测出二者间的滑动摩擦系数。进行摩擦试验的装置通常如图6所示。

试验过程中还要通过悬臂梁试验或者平板弯曲试验来测量模型冰的弹性模量和强度极限。进行悬臂梁实验时一般在冰面上将冰层切割成如图7所示的6Hi×2Hi×Hi的悬臂梁，并通过对悬臂梁的自由端加载来测得模型冰的弯曲强度σf［8］。

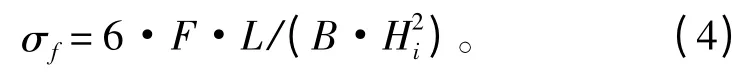
式中:F 为悬臂梁的断裂载荷;L 为梁的长度(加载点至根部);B 为梁的宽度(根部处);Hi为冰的厚度。

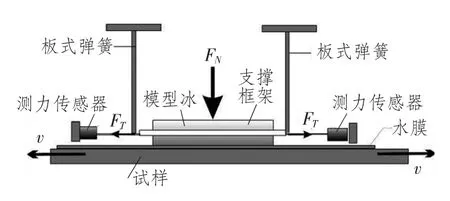
图6 摩擦试验装置图Fig.6 Friction testing apparatus

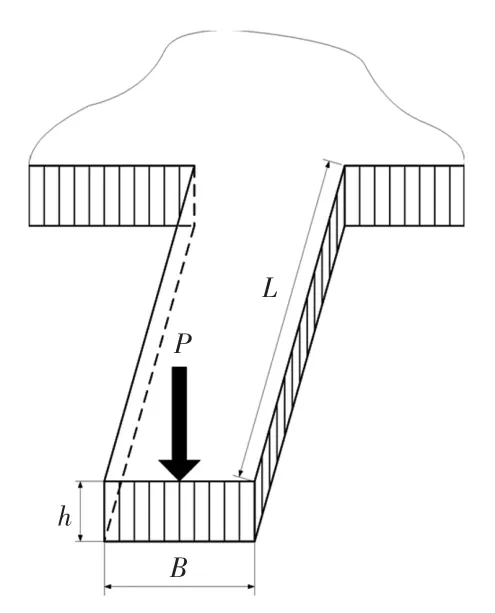
图7 悬臂梁概念图Fig.7 Conceptual figure of cantilever beam test

根据梁上分布的位移探测装置可以得到梁的挠曲线，并推出模型冰的弹性模量(图8)。为了保证模型冰的质量，每次实验后都需重新测量模型冰的弹性模量。

冰层的密度也是模型冰的重要性质之一。一般需要选取一块矩形试样，通过测量样本干舷与厚度的比值可以根据式(5)得到冰的密度。

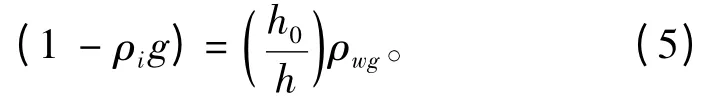
图8 悬臂梁试验装置图Fig.8 Cantilever beam test apparatus

式中:h0为样本的干舷(见图9)，水面以上任一平面距离试样顶部的距离L0与其距离水面的距离L1作差即为试样的干舷［9］;h 为模型冰试样的总高度。

图9 干舷法概念图Fig.9 Conceptual figure of the free board method

冰池试验的设备和数据记录与常规拖曳水池试验类似，但是冰池试验中因为要进行冰层断裂模式的观察和海冰运动的研究，从而需要使用放置于多个方位的摄像机对试验过程进行记录。

目前的破冰船模型试验技术虽然已经能够满足阻力测量的要求，现有试验技术却难以满足对模型冰断裂韧性的相似性要求。同时，试验中需要用到大型的制冷设备，冰层的冻结也会花费大量时间。这不但使冰池试验的成本相比普通的船模试验大为提高，也增加了试验的准备时间。另外，由于制冰过程中的环境条件难以控制，冰层的性质会因为温度的扰动，以及表面的气流等因素影响，与试验的目标值存在微小的偏差。因此，当前的冰池试验技术仍然有待改进。

3 理论预报

破冰船的理论预报方法分为分析方法和数值方法2 种［10］。其中分析方法采用经验或半经验公式对冰阻力数值进行预报，而数值方法则借助计算机程序对冰阻力数值进行求解。

3.1 分析方法

分析方法靠研究船体所受冰载荷与各变量之间的关系，对各个参数之间的关系做出一些基本假设，再以此为基础通过对于实船试验或模型试验数据的回归分析得到公式中的经验系数，最终形成完整的阻力计算经验公式或半经验公式。分析方法的准确性与样本数据有很大关系，船型与试验采用的母型船相近时结果较为准确，船型相差较大时则结果偏差较大。另外早期的经验公式大多存在不合理的假定［11］，因此多数经验公式的可靠性较差。

随着冰阻力研究的深入，后来出现了更为复杂的半经验公式。这些半经验公式结合了对于破冰过程的理论分析，并将大量相关的影响因素引入到了公式中。这些公式已经可以较为准确地反映出不同设计参数对于冰阻力的影响趋势，对破冰船的设计选型具有一定的指导意义，也有助于减少模型试验的工作量，进而节省设计成本。

分析方法中出现较早的是Jansson 于1956年给出的冰阻力估算的简化公式。但是该公式并没有为人们所广泛接受。1970年Lewis和Edwards［12］在前人工作的基础上推出了破冰阻力计算公式并得到较好的阻力计算结果。之后于1972年由Enkvist［13］提出的计算方法也得到了较好的应用。这一时期的经验公式还有Lewis 公式和改进的Edwards 公式等。

这些早期公式的理论模型尚不完善，公式中的影响因素也相对较少。所以，这些公式往往不能正确地反映冰阻力同各项影响因素之间的关系。

1973年，Milano［14］尝试将理论分析应用于冰阻力的计算上。根据结构理论和全尺度试验的观测结果将海冰假定为按照固定的模式弯曲，他的海冰破坏模型为后来的大量半经验公式开辟了道路。

1979年，Enkvist［11］指出海冰的破碎是包含挤压、剪切和挠曲等多种破坏的复杂破坏形式，同时为了简化冰阻力的计算，他将破冰船的阻力划分为破冰阻力、浸没阻力和摩擦阻力3个部分。

1989年，Lindqvist［15］结合Enkvist的工作提出了Lindqvist 公式。公式针对破冰阻力基于结构力学模型进行了分析，给出了破冰阻力的计算公式。公式还考虑了首柱处挤压破坏造成的阻力，并使用经验系数给出了具体的计算公式。

破冰阻力Rc:

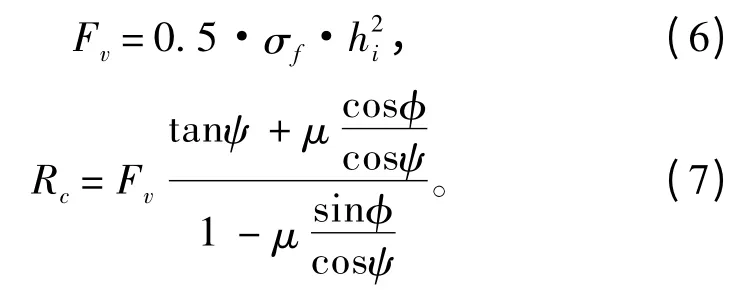
弯曲阻力RB:

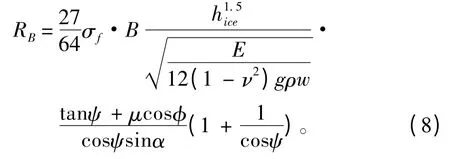
式中:hice为冰厚;E 为杨氏模量;ν 为泊松比;σf为弯曲强度;B 为船宽;ρw为海水密度。

浸没阻力Rs:

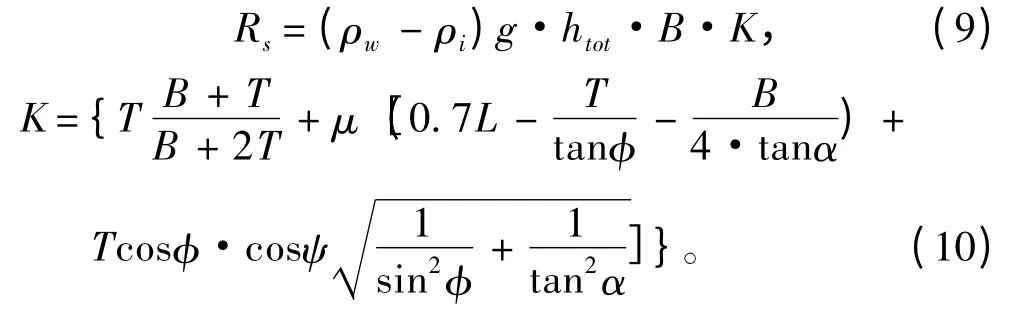
式中:ρi为冰密度;htot为冰与雪的厚度和;T 为温度;B为船宽。

总的冰阻力Ri:

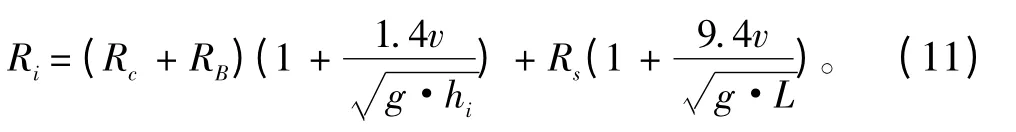
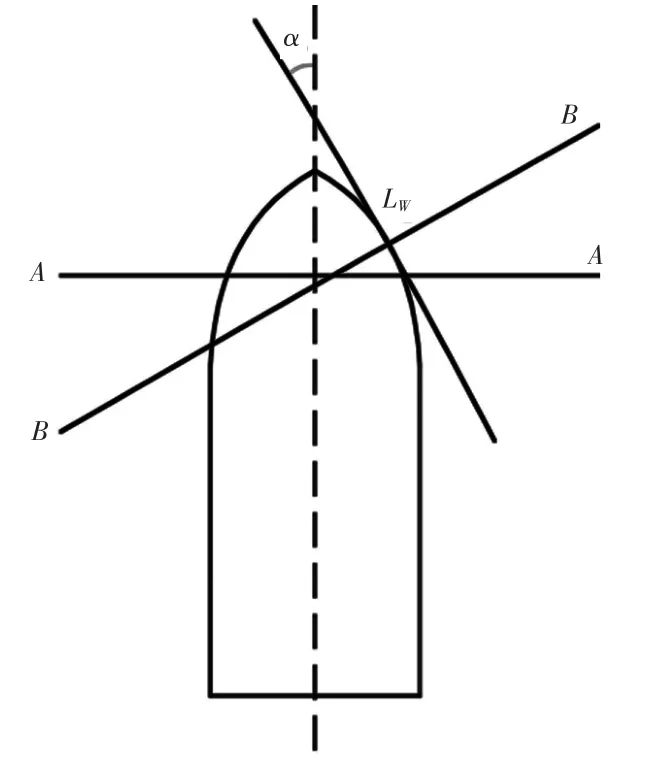
图10 水线进角示意图Fig.10 Water entrance angle

该公式的提出不但提高了经验公式的准确程度，而且公式在对传统楔形船首和匙型船首的计算结果对比中，很好地反映出了船首形状对于冰阻力的影响，因此在之后得到了广泛的应用。

1991年，Daley［16］提出了破冰活动周期的概念。他根据全尺度试验和模型试验中对于冰层破坏过程的观测，将冰层的破坏简化为挤压破坏，弯曲破坏和冰层破碎3个不断循环的过程。

Daley的接触模型虽然对冰层的破坏过程进行了一定的简化，但是这种破冰过程中的周期性规律却与实验结果基本吻合，而且将连续的破冰过程分割开来，使得冰阻力的计算模型得到了简化。

1997年，由Riska 等［17］提出了Riska 公式，公式在原有的经验公式基础上做了改进，并根据波罗的海的大量实船数据分析得出了公式的经验系数。实际应用证明，该公式对于波罗的海航行的破冰船能够得到较为准确的结果。

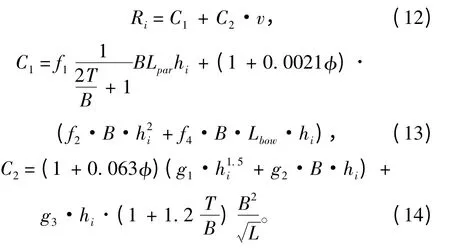
式中:L，B，T 分别为船长、船宽和吃水;V 为航速;hi为冰厚;φ 为首柱倾角，(°);Lpar和Lbow分别为平行中体长和首部长度。经验系数如表2所示。

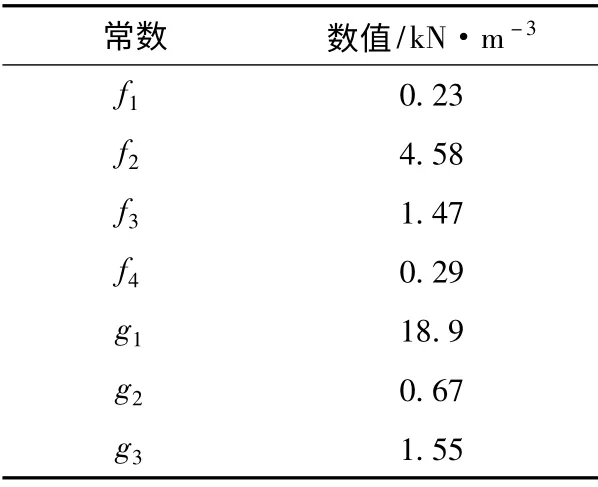
表2 Riska 公式常数表Tab.2 Constants in Riska formula

虽然随着冰阻力研究的深入，冰阻力的计算模型已经得到了长足的进步，但是经验公式和半经验公式普遍将冰阻力和敞水阻力区分为2个独立的阻力成分而忽略了二者之间的耦合作用［11］。同时，在公式中普遍采用的冰阻力成分划分方法虽然能帮助人们简化冰阻力的计算，却难以在试验中测得各个成分的准确数值，这使得各阻力成分的经验系数不够准确。加之公式包含的参数有限，使得各参数的变化对公式准确性有着显著的影响［18］。

也有部分公式为了计算的简便，过分简化了船体表面和冰层边缘的几何形状和二者的接触形式。此外，经验公式虽然能够较为准确地预报常规的破冰船在平整冰中航行时的阻力大小，对于破冰船经过冰脊或与冰山碰撞等特殊情况下受到的阻力却无法进行准确的预报，因此适用范围也较为有限。虽然其中的一部分公式得到了实验数据的支持并且直到现在还被广泛运用，却只能够用于设计阶段的船型选择，不足以替代模型试验。

3.2 数值方法

由于以上原因，近几年来人们建立了许多数值方法以提高冰阻力计算方法的准确性和可靠性。在这些数值模拟方法中应用最多的是有限元方法(FEM)和离散元方法(DEM)。根据这些数值模拟方法，计算机不但可以将破坏模式的影响考虑在内，还能比经验公式更加明确地反映出船体首部形状变化等因素所导致的阻力改变。为了发挥计算机强大计算性能的优势，这些数值模型也比经验公式所采用的模型复杂的多，因此模型中作的简化相对较少，结果也比经验公式更为准确。

这其中有限元方法的应用则稍早于离散元方法，是由Määttänen和Hoikkanen 在1990年最先应用于冰载荷模拟上的;近年来，Konuk 等 (2009)，Kolari 等(2009)和Ranta et 等(2010)也相继对有限元方法在冰载荷模拟上的应用进行了研究。

1992年，Evgin 等最先将离散元方法用于冰载荷的模拟，其后的Hopkins (1997)和Paavilainen et al.(2006)等也对离散元方法进行了进一步的研究。

但是受制于早期计算机的计算能力，当时的数值模型相对于经验公式而言并没有显现出特别的优势，直到近来随着人们对于破冰船破冰机理研究的深入和计算机性能的飞速发展，使得具有复杂计算模型的数值方法显现出了前所未有的优势，这才令冰阻力计算的数值模拟方法成为了人们研究的热点。

2001年，Valanto［19-20］提出了一个3D 有限元模型。在该模型中考虑了冰面下水流的流体动力学作用对于冰层破坏的影响。此外Valanto 还指出可以通过欧拉- 拉格朗日公式对冰层破坏产生的碎冰进行建模，这进一步促进了浸没阻力和摩擦阻力的直接计算方法的发展。2001年Wang［21］提出了一种求得时域解的计算方法，计算模型中通过几何网格来模拟固定的圆锥与移动的冰层之间的连续接触过程。2011年Vegard Aksnes［22］提出了一种用于计算平整冰对系泊船只作用的半经验数值计算方法。该方法将冰的运动分为水线附近的冰层破坏、碎冰翻转以及水线以下由于冰与船体摩擦产生的运动，船体则被离散为平板。且最终计算得到的结果与模型试验数据比较后证明了该方法具有较好的准确性。2013年Xiang Tan 等［23］提出了一个描述冰与船体之间相互作用的六自由度模型，从而将船体的升沉、横摇和纵摇运动加入了模型的考虑范围。

时至今日，人们已经提出了多种用于计算破冰船阻力的数值方法，上述的众多方法中以有限元方法较为成熟。通常用于计算平整冰条件下冰阻力的有限元方法会在每一个时间步长内依照船体受力计算、运动方程求解、更新水线位置、接触判定、受力计算、冰层破坏的循环进行。

不同的有限元程序对于冰阻力问题的求解流程虽然相似，但其受力计算公式和冰层破坏的判定却有很大的差异。至于离散元方法，其主要应用于碎冰条件下的冰阻力计算，因此在完成初始设置和船体与碎冰间的接触判定后需要对水域中碎冰的受力进行计算，据此得到各个离散元的运动方向和速度，确定其下一时间步长内的位置。

然而数值方法的出现并没有完全解决分析方法中所存在的问题。尽管通过计算机的辅助，人们得以采用更为复杂的计算模型，其计算过程仍然涉及到冰层的破碎以及冰与海水间的流固耦合问题。为了避免复杂的问题，目前仍有大量的数值方法采用经验公式的理论模型来对问题进行简化，致使这些数值方法难以摆脱传统分析方法的限制。

除了传统的有限元方法和离散元方法，随着近年来数值计算方法的迅速发展也有许多崭新的数值方法被用于冰阻力的计算。2004年，Munjiza［24］结合了有限元和离散元2 种方法的优点，提出了FEM– DEM 方法。通过FEM – DEM 方法可以运用有限元方法来模拟冰层的碎裂并使用离散元方法来模拟碎冰的堆积过程，这样就可以结合2 种方法的优势对破冰过程进行计算，得到更为准确的结果。2009年，Polojärvi和Tuhkuri［25］首先将该方法应用于冰脊龙骨的冲撞模拟中。这一尝试不但发展了FEM-DEM 方法在研究破冰过程方面的应用，而且推进了数值模型在模拟冰脊等特殊条件下的应用。

尽管目前的数值仿真方法获得的冰阻力计算结果还不尽如人意，但是相比经验公式而言，数值仿真方法便于对船体和冰层形状进行细致的描绘并一定程度上计入流体动力学作用对冰阻力的影响。而随着人们对于冰阻力研究的深入，数值方法也在不断完善。因此，数值方法的研究有着广阔的前景。

4 结 语

破冰船的阻力问题是影响破冰船能否满足其设计破冰能力的关键问题之一。国外在冰阻力的研究上已经形成了成熟的理论体系，但是由于国内对破冰船领域的关注较晚，这一领域的研究尚在起步阶段。

本文就破冰船阻力研究的几种主要方法进行了简要的介绍，对不同方法的发展现状、自身优势、现存问题及发展方向进行了简要的分析与论述，对相关的研究者有一定的借鉴意义。

［1］TIMCO G W，O.BRIEN S.Flexural strength equation for sea ice［J］.Cold Regions Science and Technology，1994，22:285-298.

［2］孟广琳.国外模型冰槽及冰中海上结构物的物理模拟［J］.海洋环境科学，1986(1):85-95.MENG Guang-lin.Physical simulation of foreignmodel ice tank and offshore structures［J］.Marine Environmental Science，1986(1):85-95.

［3］TIMCO G W.The mechanical properties of saline-dopedand carbamide (urea)-doped model ice［J］.Cold Regions Science and Technology，1980，3(1):45-56.

［4］王永学，李志军，李广伟.DUT-1 非冻结合成模型冰物模技术及应用［J］.大连理工大学学报，2001(1):94-99.WANG Yong-xue，LI Zhi-jun，LI Guang-wei.Technique of DUT- 1 non-refrigerated breakable ice materials and its applications ［J］.Journal of Dalian University of Technology，2001(1):94-99.

［5］TIMCO G.The mechanical and morphological properties of doped ice:A search for a better structurally simulated ice for model test basins［C］//POAC 79，Proceedings，1979:719-739.

［6］史庆增，徐继祖，宋安.冰力模型实验［J］.冰川冻土，1990(2):117-123.SHI Qing-zeng，XU Ji-zu，SONG An.The model test of ice forces［J］.Journal of Glaciology and Geocryology，1990(2):117-123.

［7］TIMCO G W.EG/AD/S:A new type of model ice for refrigerated towing tanks［J］.Cold Regions Science and Technology，1986，12(2):175-195.

［8］SCHWARZ J，FREDERKING R，GAVRILLO V，et al.Standardized testing methods for measuring mechanical properties of ice ［J］.Cold Regions Science and Technology，1981，4(3):245-253.

［9］RISKA K，KATO K M，BELJASHOV M V，et al.Report of the performance in ice-covered waters committee 21st［R］.1996.

［10］TIMCO G，CROASDALE K，WRIGHT B.An overview of first-year sea ice ridges［R］.PERD/CHC report，2000.

［11］ENKVIST E，VARSTA P，RISKA K.The ship-ice interaction ［C］//POAC 79， Proceedings of the 5th International Conference on Port and Ocean Engineering under Arctic Conditions.1980，2.

［12］LEWIS J W，EDWARDS Jr R Y.Methods for predicting icebreaking and ice resistance characteristics of icebreakers［R］.1970.

［13］ENKVIST E.On the ice resistance encountered by ships operating in the continuous mode of icebreaking［R］.1972.

［14］MILANO V R.Ship resistance to continuous motion in ice［D］.Stevens Institute of Technology，1972.

［15］LINDQVIST G.A straightforward method for calculation of ice resistance of ships［C］//Proceedings of POAC.1989:722-735.

［16］DALEYC G.Ice edge contact- a brittle failure process model［R］.1991.

［17］RISKA K.Performance of merchant vessels in ice in the Baltic［M］.Sjäfartsverket，1997.

［18］THORSEN I B.Estimation and computation of ice-resistance for ship hulls［D］.Norwegian University of Science and Technology，2012.

［19］VALANTO P，JONES S J，ENKVIST E，et al.The resistance of ships in level ice.Discussion.Author ＇s closure［J］.Transactions-Society of Naval Architects and Marine Engineers，2001，109:53-83.

［20］VALANTO P.On the cause and distribution of resistance forces on ship hulls moving in level ice［C］//Proceedings of the 18th International Conference on Port and Ocean Engineering Under Arctic Conditions，Ottawa，Ontario，Canada.2001:803-813.

［21］WANG S.A dynamic model for breaking pattern of level ice by conical structures ［J］.Acta Polytechnica Scandinavica Mechanical Engineering Me，2001，156.

［22］AKSNES V.A panel method for modelling level ice actions onmoored ships.Part 1:Local ice force formulation［J］.Cold Regions Science and Technology，2011，65(2):128-136.

［23］TAN X，SU B，RISKA K，et al.A six-degrees-of-freedom numerical model for level ice-ship interaction［J］.Cold Regions Science and Technology，2013，92:1-16.

［24］XIANG J，MUNJIZA A，LATHAM J P，et al.On the validation of DEM and FEM/DEM models in 2D and 3D［J］.Engineering Computations，2009，26(6):673-687.

［25］POLOJARVI A，TUHKURI J.3D discrete numerical modelling of ridge keel punch through tests［J］.Cold Regions Science and Technology，2009，56(1):18-29.