基于SST湍流模型的某弹体出水过程流场数值研究

邬 明

(中国船舶重工集团公司 第七一〇研究所，湖北 宜昌443003)

0 引 言

潜射导弹以其隐蔽性等优势为各大军事强国所重视。经潜艇发射后，弹体需要跨越水介质至空中再进入预定弹道［1-3］。从水介质进入空气介质的力学突变对出水弹道产生极大影响［4］，因此获得准确的流体动力系数，对弹道设计至关重要。

随着计算性能的快速提高和计算数学理论的不断发展完善，数值方法已经成为研究问题和解决问题的重要手段之一，它不仅在理论研究领域得到普遍应用，而且在工程实际中也被广泛使用。求解雷诺平均N-S 方程式是当前数值计算的主要方法，需补充湍流模型对方程进行封闭。湍流模型对于数值模拟空化流场的精度具有决定性影响。当前应用最普遍的湍流模型是k-ε湍流模型，然而该模型有以下不足之处:在模型中湍流尺度未知;仅限于湍流边界层压力相对稳定的情况;其壁面函数在边界层的修正中难以弥补计算模型与实际现象之间的差距。相对于k- ε湍流模型的以上不足之处，SST k-ω湍流模型［5］却拥有以下优点:该模型能够适应逆压梯度变化的各种物理现象;可应用于粘性内层，通过对壁面函数的应用，能够精确的模拟边界层的现象，无需使用较容易失真的粘性衰减函数。本文将SST k- ω湍流模型应用于弹体出水过程流场的仿真分析中，取得了较好的结果。

SST k- ω湍流模型以下简称SST湍流模型。

1 控制方程与算法

1.1 连续方程

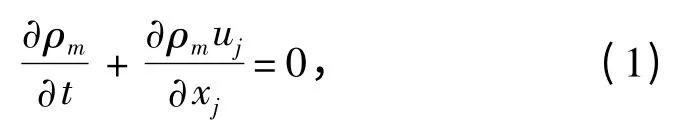
式中:ρ 为密度;U 为速度;t 为时间。

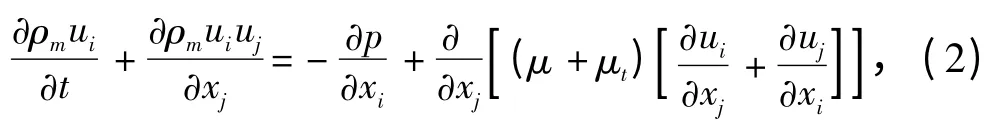
式中:ρm=ρlαl+ ρv(1- αl);;μt和αl分别为流体动力粘度和水相的体积分数。

1.2 湍流模型

若分别以φ1，φ2，φ3表示k-ω 模型、k-ε 模型和SST湍流模型中的函数关系，则SST湍流模型可表示为:

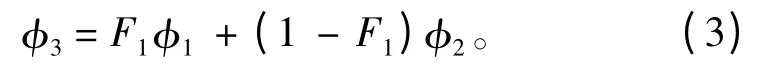
其中

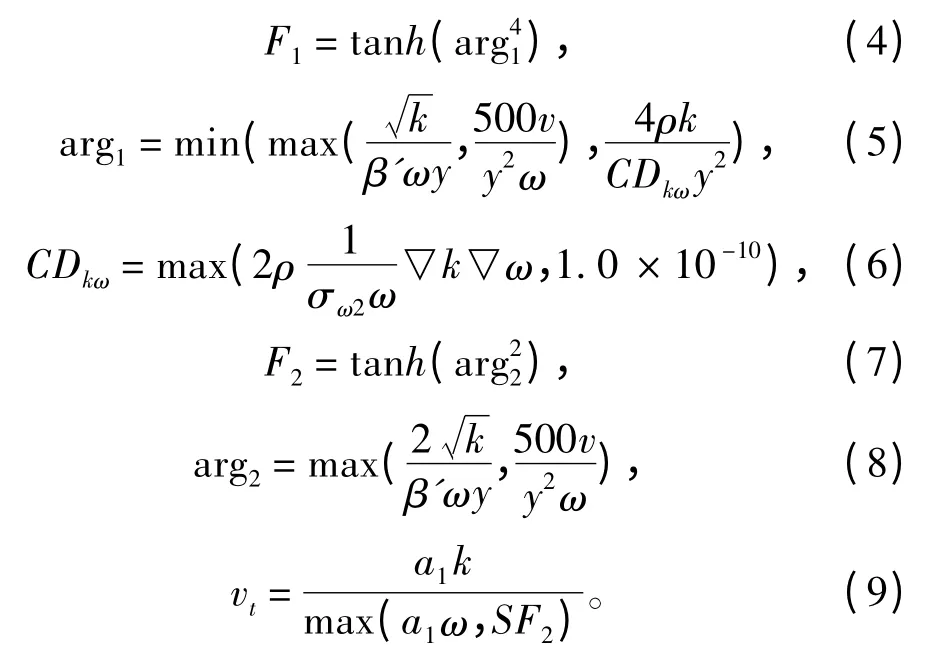
SST湍流模型考虑到湍流剪切应力的输运，不但能够对各种来流进行准确的预测，还能在各种压力梯度下精确模拟分离现象，其综合了近壁面k- ω模型的稳定性及边界层外部k- ε 模型独立性的优点，它的计算模拟性能优于后两者。各系数取值为β′=0.09，α1=5/9，β1=0.075，σk1=2，σω1=2，α2=0.44，β2=0.0828，σk2=1，σω2=1.168，各个数据的取值取自参考文献［6］。

2 物理模型

某型弹体的形状和尺寸示意图如图1所示。其长度为7.3 m，直径为0.534 m，弹体为截体半椭球(半长:0.534 m，截掉0.034 m)。

针对出水过程流场在不同运动阶段的流体动力特性，本文利用切片法对不同出水长度下的流场进行仿真分析。弹体长度为7 300 mm，这里考虑出水过程的8 种工况，即出水长度0 m、1.5 m、2.5 m、3.5 m、4.5 m、5.5 m、6.5 m、7.3 m 且每个工况对应有攻角0°～18°，计算出每种工况下的流体动力系数，包括阻力系数、升力系数和力矩系数，并得出其变化规律。

图1 某弹体外形图Fig.1 Outline of projectile

3 计算区域和网格划分

计算网格的好坏直接影响到数值计算的可行性、收敛性以及计算精度。前处理软件ICEM CFD 是一款成熟的网格划分软件，它向用户提供业界领先的高质量网格技术，其强大的网格划分功能可以满足CFD 仿真计算的严格要求。

对于本文中的问题若采用非结构网格，生成的空泡边界会出现凹凸不平的毛刺，影响对仿真结果的分析。若想消除毛刺现象，就要对网格进行细分。因此采用基于六面体结构化网格划分方法，对计算区域进行全六面体结构网格划分，并利用与湍流强度相关的Yplus 对所建模型进行考核。弹体网格图如图2所示。

图2 弹体网格图Fig.2 Grid graph of missile

4 仿真计算结果及分析

4.1 压力分布

图3和图4 给出了弹体表面压力云图和表面压力系数分布曲线。

图3 弹体压力云图Fig.3 Pressure cloud of missile

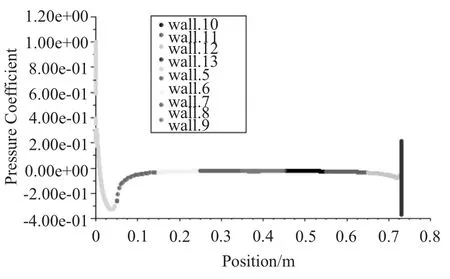
图4 弹体表面压力系数分布曲线Fig.4 Surface pressure coefficient distribution curve of projectile

4.2 流体动力系数计算结果

图5 给出了弹体在速度系下的阻力、升力和力矩随攻角的变化曲线。从图中可以看出，小攻角下(6°以内)线性良好，当攻角较大时，线性假设将会导致较大的误差。

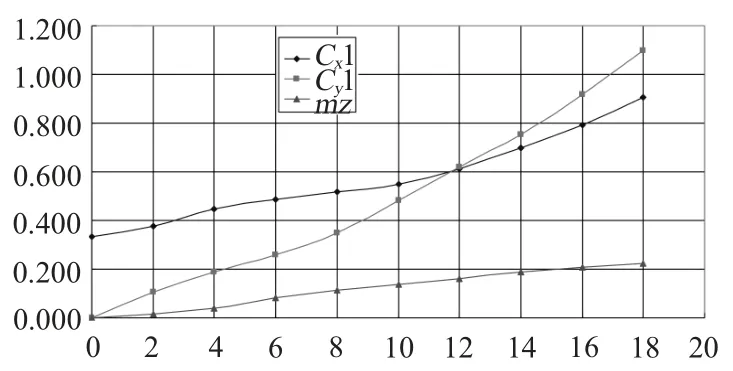
图5 全沾湿下流体动力系数随攻角的变化Fig.5 Full wet hydrodynamic coefficients of variation with angle of attack

下面给出了流体动力系数随出水长度和攻角变化的二维数表，使用时通过查表插值的方法提取任意攻角和任意出水长度下的流体动力系数，即编写插值函数Chazhi (x，alfa，＆Cx，＆Cy，＆mz)

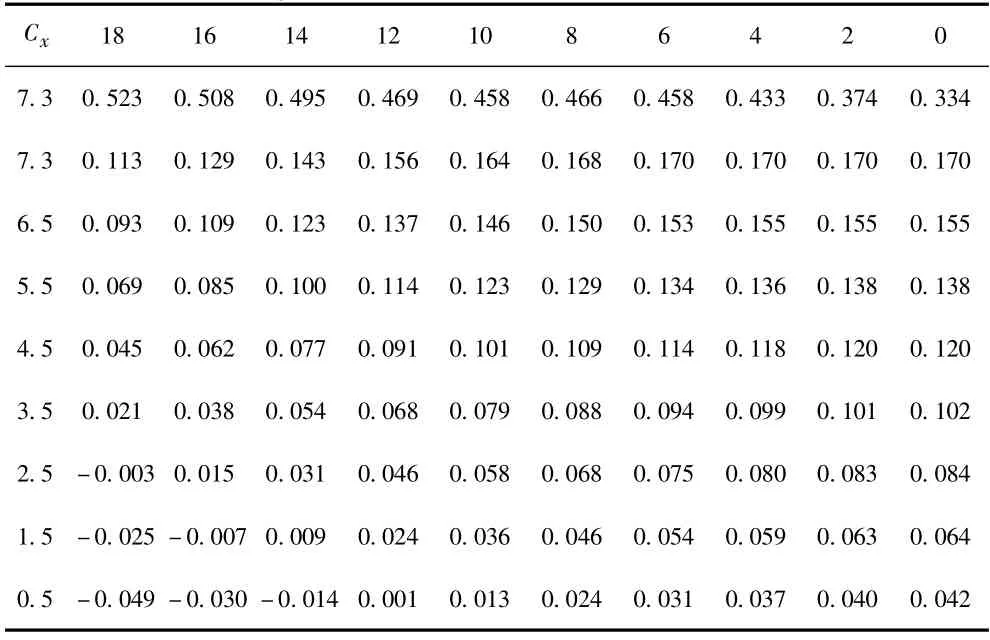
表2 阻力系数随攻角及出水长度的变化Tab.2 Variation of drag coefficient with angle of attack and the length of the water

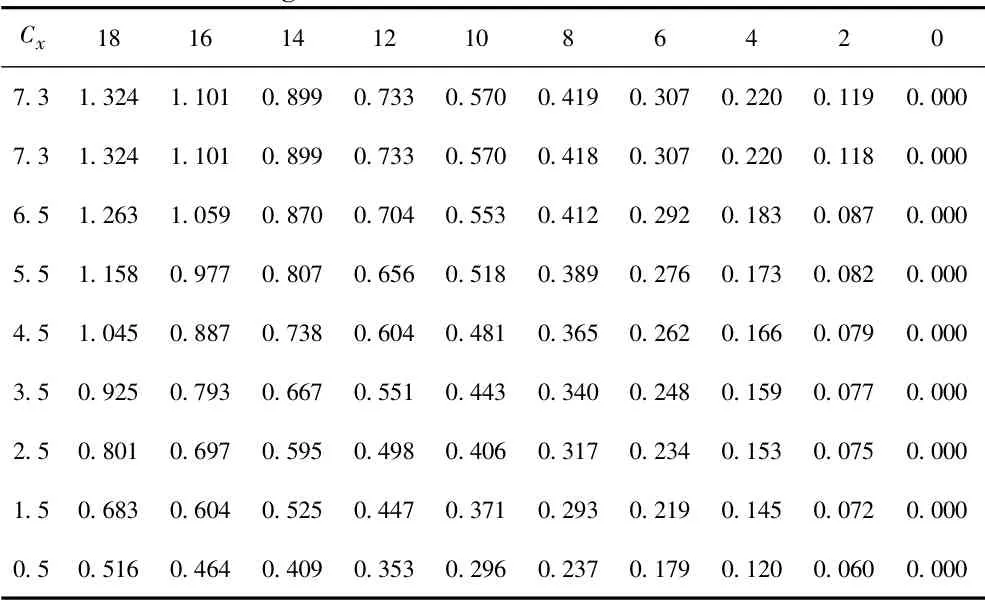
表3 升力系数随攻角及出水长度的变化Tab.3 Variation of lift coefficient with angle of attack and the length of the water

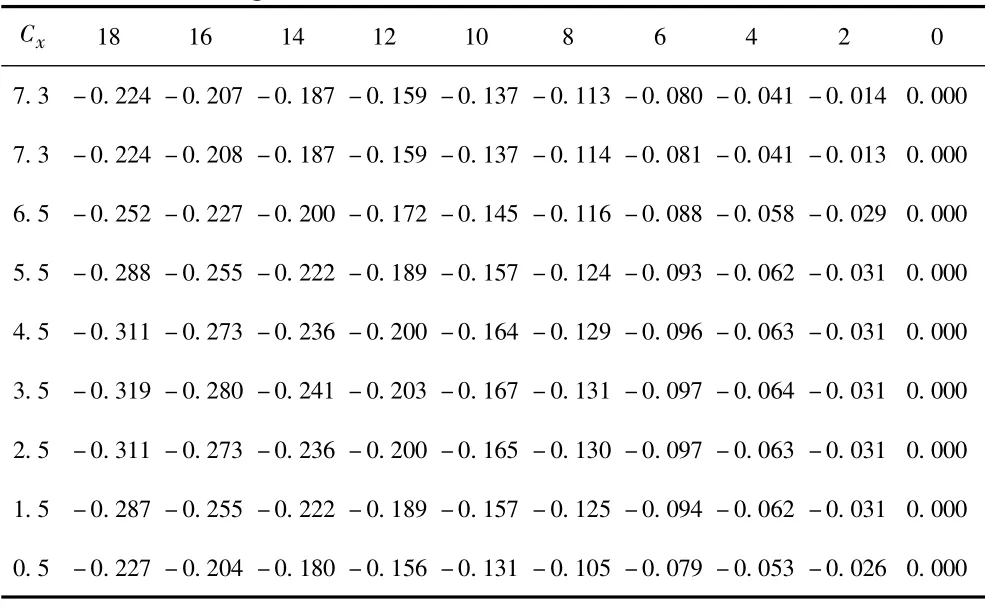
表4 力矩系数随攻角及出水长度的变化Tab.4 Moment coefficient with angle of attack and the length of the water

出水过程流体动力系数随出水长度和攻角的变化规律如图6～图8所示。

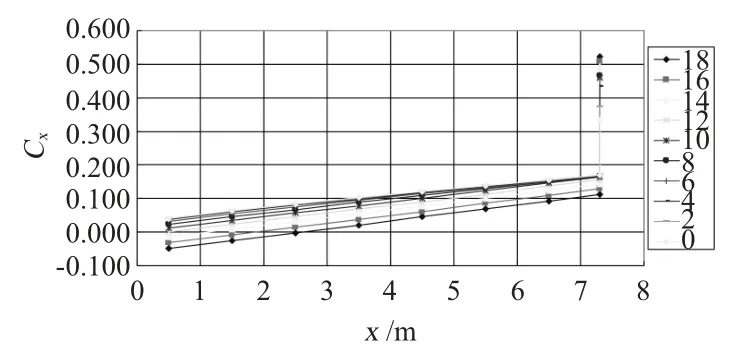
图6 不同攻角下阻力系数随出水长度的变化曲线Fig.6 The drag coefficient with water under different angles of attack

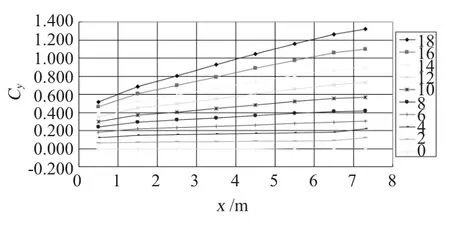
图7 不同攻角下升力系数随出水长度的变化曲线Fig.7 The lift coefficient with water under different angles of attack

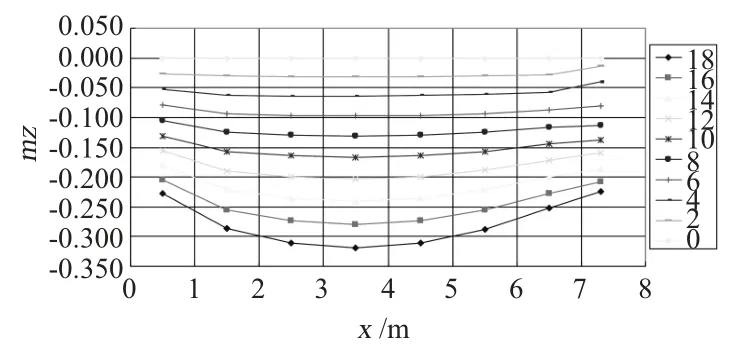
图8 不同攻角下力矩系数随出水长度的变化曲线Fig.8 Moment coefficient with water under different angles of Attack

在6°范围内(相关资料记载，小攻角下流体动力参数具有较好的线性性，大攻角则出现复杂非线性)给出数值计算与实验结果的比较。

表5 数值计算与实验的对比Tab.5 Comparison of numerical and experimental

5 与航天部公式的比较

方法:使用计算得到的全弹轴向力、法向力和俯仰力矩系数，乘以航天部提供的出水系数公式，得到的数表与本文提供的数表进行对比分析。图9～图11 给出了无量纲化后阻力、法向力和力矩影响系数随攻角及出水长度的变化曲线。

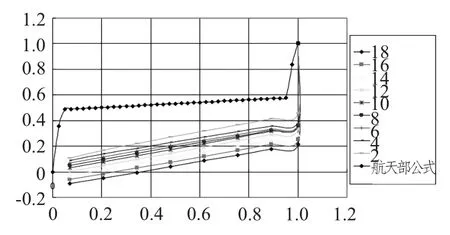
图9 不同攻角下阻力影响系数随出水长度的变化曲线Fig.9 Drag coefficient with water under different angles of attack

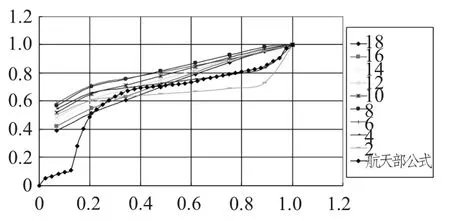
图10 不同攻角下法向力影响系数随出水长度的变化曲线Fig.10 Force dismount influence coefficient varies with water under different angles of attack

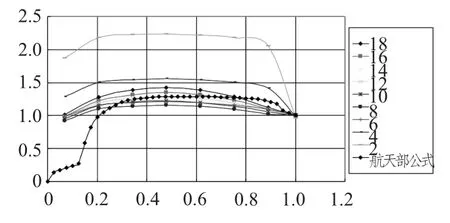
图11 不同攻角下力矩影响系数随出水长度的变化曲线Fig.11 The influence coefficient torque with water different angles of attack

从图9～图11 可发现，文章的计算结果与航天部给的公式能够很好的吻合在一起，具有较高的工程应用精度。

6 结 语

采用SST湍流模型，文章对弹体出水过程流体动力特性进行了详细的分析，并与相关资料进行比较研究，结果表明:运用N-S 方程及SST湍流模型对均质流场求解，并利用切片仿真方法，对弹体出水过程进行数值模拟，与相关资料取得较好的一致性，证明了所选湍流模型的可行性，为以后的弹道规划和控制系统设计提供了科学依据。

［1］程载斌，刘玉标，刘兆.导弹水下潜射过程的流体-固体耦合仿真［J］.兵工学报，2008，29(2):178-183.CHENG Zai-bin，LIU Yu-biao，LIU Zhao.Fsi simulation on the vertical launching process of underwater missile［J］.Acta Armamentarii，2008，29(2):178-183.

［2］崔乃刚，曹春泉，韦常柱.潜射导弹水下运动过程仿真分析［J］.弹道学报，2009，21(2):96-97.CUI Nai-gang，CAO Chun-quan，WEI Chang-zhu.Simulation analysis of underwater motion process of submarine launched missile［J］.Journal of Ballistics，2009，21(2):96- 97.

［3］闵景新，魏英杰，王聪，等.潜射导弹垂直发射过程流体动力特性数值模拟［J］.兵工学报，2010，31(10):21-27.MIN Jin-xin，WEI Ying-jie，WANG Cong，et al.Number simulation on hydronamic characteristics of submarine missile in the vertical launch process ［J］.Acta Armamentarii，2010，31(10):21-27.

［4］刘乐华，张宇文，袁绪龙.潜射导弹垂直出水流场数值研究［J］.弹箭与制导学报，2004，24(2):89-91.LIU Le-hua，ZHANG Yu-wen，YUAN Xu-long.Numerical stidy on a submarine-launched missile vertically exited form water［J］.Journal of Projectiles Rockets Missiles and Guidance，2004，24(2):89-91.

［5］王福军.计算流体力学分析- CFD 软件原理与应用［M］.北京:清华大学出版社，2004，2-2，117.

［6］Fluent Inc，FLUENT User＇s Guide.Fluent Inc，2013.