酉群与正交群和辛群之间的关系
2015-12-03
(临沧师范高等专科学校 数理系,云南 临沧 677000)
1 预备知识
历史上对群的研究最早是从置换群和变换群开始的,1771年Lagrange 自发地采用置换群以解决用根式解代数方程的问题.1799年Ruffin,1824年Abel 继续这一工作,直到1830年,Galois 自觉地应用群的思想(群的术语就是他首先引进的)彻底解决了这一问题,1872年推出了著名的Erlangen 纲领,用对变换群来对几何学分类.到19世纪末,人们意识到,在数学的不同领域中独立存在的群论思想,在原则上是统一的.这种想法引起了研究抽象群的概念.Kelly,Frobenius,Dyck 等最早从事抽象群的研究,Schmidt 于1916年出版了《抽象群论》一书.于是群论成为代数学的一个重要分支,而有些不同的典型群之间有着密切关系,搞清楚他们之间的关系是非常有必要的.
n 维欧几里得空间V 上所有正交变换组成的集合只有一种运算:乘法,它满足结合律,恒等变换属于这个集合,这个集合的任一元素可逆且逆元素也在这个集合中.类似地,n 维酉空间上所有酉变换组成的集合,域F 上n 维正则的正交空间上所有正交变换组成的集合,特征不是2的域F 上2r 维正则辛空间上所有辛变换组成的集合都具有这样的性质.
定义[1]设G是一个非空集合,如果在G 上定义了一种代数运算,叫做乘法并且满足以下法则:
1° a(bc)= (ab)c,a,b,c ∈G(结合律)
2° G 中有一个元素e,使得ea=ae=a,a ∈G
3° 对于G 中每一个元素a,都有G 中一个元素b,使得ab=ba=e,那么G 称为一个群.
实数域上所有2r级正交矩阵组成的集合对于矩阵乘法构成一个群,称它为实数域上的2r级正交群,记录O(2r).
所有r级酉矩阵组成的集合对于矩阵乘法组成的一个群,称它为r级酉群,记为U(r).
特征不为的域R 上2r级辛矩阵的全体,对于矩阵乘法组成一个群,称它为2r级辛群,记作Sp(2r,R).
2 主要结论
结论 U(r)= O(2r)∩Sp(2r,R).
证明 r 维复线性空间Cr中元素X=(a1+b1i,…,ar+bri)'可以写成

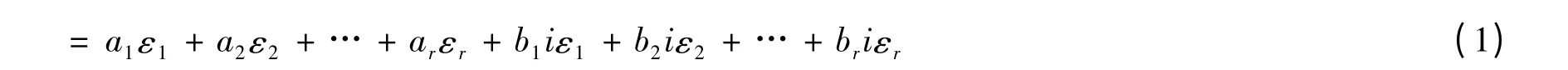
于是Cr可以看成是2r 维实线性空间,记作V,它是一个基为ε1,ε2,…,εr,iε1,iε2,…,iεr.于是同一个记号C 即可表示r 维复线性空间Cr的元素,又可表示2r 维实线性空间V的元素.
任给一个r级复矩阵P,可定义复线性空间Cr上的一个线性变换P:P(X)= PX,X ∈Cr,又可定义2r 维实线性空间V 上的一个线性变换珘P:

在复线性空间Cr中定义标准内积(即X,Y)c=Y*X 成为一个酉空间.
在2r 维实线性空间V 中定义内积如下:设

规定

则V 成为一个2r 维欧几里得空间.
在2r 维实线性空间V 中,定义一个双线性函数f,它在V的基ε1,…,εr,iε1,iε2,…,iεr下的度量矩阵A为

由于A是可逆斜对称矩阵,因此f是非退化的斜对称双线性函数.从而(V,f)成为一个2r 维正则辛空间,f是(V,f)上的辛内积,对于上述X,Y,有

于是有

设P是Cr上的线性变换,按前面所述,它也表示V 上的一个线性变换,利用(5)式可以得出:

因此在对于有两种理解的约定下,我们可以写成

由于U(Cr)U(r),O(V)O(2r),Sp(V,f)Sp(2r,R).因此在上述约定下,可以写

对于(6)式的理解如下:任给一个r级酉矩阵P,可以按上述方法得到一个2r级正交矩阵Q,并且Q是2r级辛矩阵;反之,任给一个2r级正交矩阵Q,如果Q 也是2r级辛矩阵,那么可得到一个r级酉矩阵P.
证明揭示了酉群U(r)与正交群O(2r)和辛群Sp(2r,R)之间的关系,这是很深刻的一个结果.证明的关键之一是把r 维复线性空间Cr看成2r 维复线性空间,记作V;关键之二是证明了(5)式,即酉空间Cr的标准内积(X,Y)C与2r 维欧几里得空间V的内积,2r 维辛空间(V,f)的辛内积之间的关系.
为了帮助读者理解结论,例如,在U(2)中取一个元素bφ,设X=(a1+b1i,a2+b2i)'∈C2.C2可看成4 维实线性空间,记作V,X可写成

C2上的线性变换bφ的定义为bφ(X)= bφX.

于是V 上的线性变换bφ在基ε1,ε2,iε1,iε2下的矩阵为

[1]丘维声.高等代数(下册)(第二版)[M].北京:高等教育出版社,2003:162-188.
[2]许莆华,张贤科.高等代数解题方法[M].北京:清华大学出版社,2001.
[3]丘维声.抽象代数基础[M].北京:高等教育出版社,2003.
