轮辐通风孔结构对车轮风阻及通风性能的影响
2015-12-03梁玄勇
康 宁,梁玄勇
(北京航空航天大学交通科学与工程学院,北京 100191)
汽车车轮周围流场对汽车整车空气动力性能有着重要的影响,车轮相关的气动阻力在整车的气动总阻力中占有相当的比重,同时汽车在制动行驶过程中,尤其对于一些重型车辆,由于制动时摩擦生热,使制动装置上产生高温,导致刹车失灵,还会使轮胎温度升高,加速轮胎老化,甚至引起轮胎着火、爆胎等严重事故.所以,对车轮风阻及通风性能的研究,有着重要的实际意义和工程应用价值.
胡兴军[1]等针对某款车轮不同辐板车轮的外流场进行研究发现,辐板的改变不仅影响车轮局部流场,还影响整车的气动特性.王国华[2]通过CFD方法分析了简化车轮辐板孔型、个数与空气动力学及车轮内的散热关系,为车轮轮辋孔型、结构方面的设计提供了理论依据.芦克龙[3]分析了辐板式样、开孔数量和面积对制动盘散热的影响.谷正气[4]研究了辐板开孔个数和面积对整车气动阻力的影响.蒋建军[5]设计了一种风冷降温式车轮,轮辐设计成扇叶型,一定程度上改善了车轮的散热效果.文献[6]对离心式、轴流式叶片车轮以及传统车轮进行了研究,结果表明离心式叶片车轮的通风量提高的幅度最大.
以上的研究主要是针对车轮辐板的式样以及通风孔的数量和面积,本文研究某型号钢制车轮通风孔开孔结构对风阻及通风性能的影响.对装在左轮及右轮上的原型和改型方案周围空气的流动现象进行数值模拟,研究经过改型设计后车轮风阻以及通过轮辐通风孔通风量的变化情况.
1 计算模型及计算方法
1.1 控制方程组
汽车车轮周围空气的流动可认为是定常三维不可压流动问题,满足如下控制方程:
连续方程
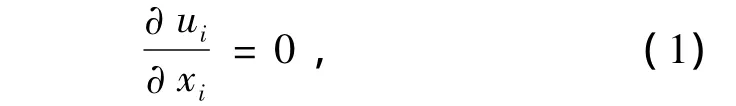
动量方程

式中:u为速度分量;p为压力;μ为动力粘性系数,ρ为密度.
1.2 车轮模型
本研究的钢制车轮由轮辐、轮辋、制动鼓及轮胎组成,车轮模型见图1.坐标系固结于车轮上,原点位于制动鼓与轮辐装配面的中心处.

图1 钢制车轮
图2给出了分别装在左轮及右轮上的原型轮辐.图中左侧箭头表示来流方向,右侧箭头表示车轮旋转方向,数字表示10个通风孔的编号.
改型轮辐是在原型基础上,对原型轮辐通风孔前后部分分别做不同方向的压凹而得到的.装在左轮上的是在通风孔前部向里压凹(前凹),后部向外压凹(后凸),装在右轮上的正好与左轮相反(前凸后凹).图3给出的是左轮改型和右轮改型的局部,其中改型轮辐编号同原型.
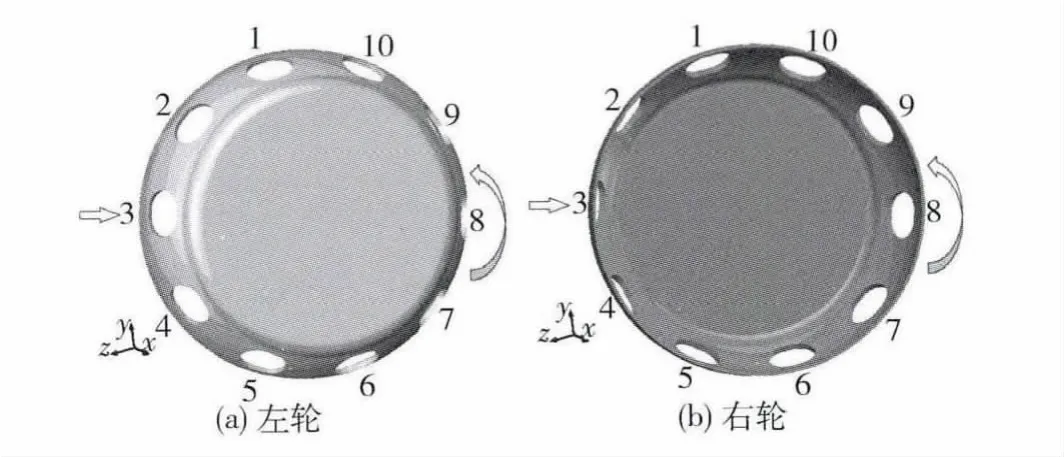
图2 原型轮辐

图3 改型轮辐
1.3 计算域模型
计算域在车轮前为2.5D(车轮直径),在车轮后为6.5D,在车轮左右两侧均为3 W(车轮宽度).由于研究的是改型车轮风阻以及通风量的变化情况,暂不考虑地面的影响,在车轮上下部均为2D,如图4所示.
为了采用动参考系模型模拟车轮的旋转问题,对包围在车轮周围的流体计算域单独命名为旋转计算域,见图4.旋转计算域内部为车轮,外部为静止计算域.
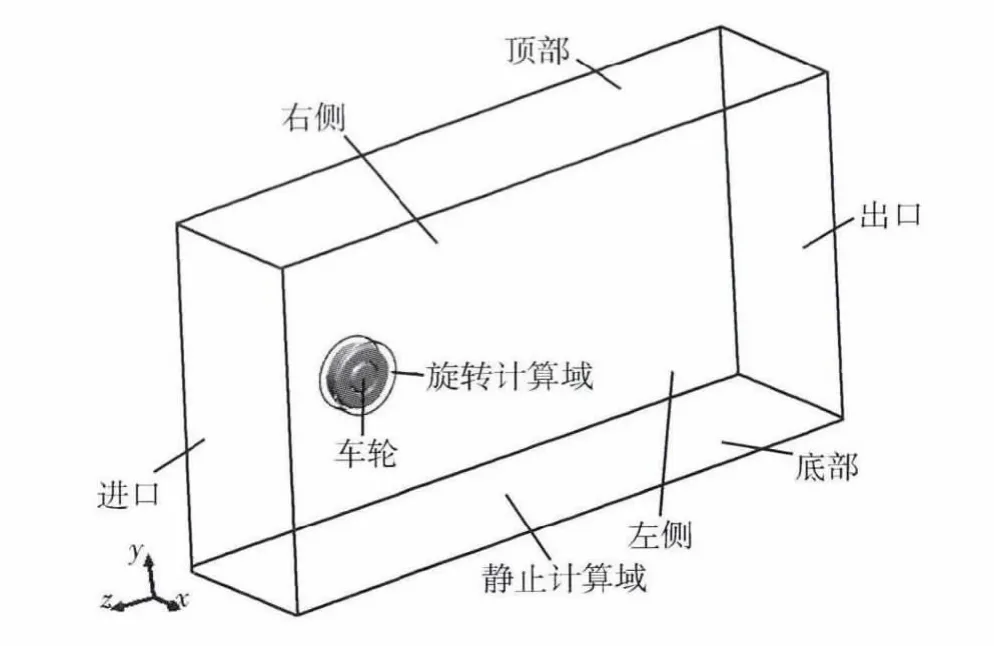
图4 计算域示意图
1.4 网格划分
由于轮辐、轮辋及制动鼓的结构比较复杂,流场变化剧烈,为了保证计算可靠性,提高计算效率,由车轮向外,网格由密到疏过渡,结构细小处还做了进一步的加密处理.
对计算域建立非结构四面体网格,网格数目在490万左右.图5为轮胎、轮辐、轮辋及制动鼓的面网格分布情况.

图5 车轮面网格分布图
1.5 物性参数及求解设置
空气密度为1.225 kg/m3,动力粘性系数为1.789×10-5kg/(m·s).
采用基于压力求解器,隐式求解方法,一阶隐式时间积分方案,标准k-ε湍流模型,SIMPLE速度和压力耦合处理方法,动量及能量方程的离散格式采用一阶迎风格式.参考压强为一个标准大气压.
1.6 边界条件
计算域中旋转计算域为旋转运动,转动中心为(0,0,0),转动坐标轴为 (1,0,0),转动角速度为31 rad/s;进口为速度入口条件,流速为汽车行驶速度16.67 m/s;出口为压力出口条件,表压为0;计算域左右两侧、顶部和底部均为滑移平动壁面条件,运动速度同进口;轮辐、轮辋、制动鼓及轮胎表面均为无滑移旋转壁面条件,旋转情况同旋转计算域,见图4.
2 计算方法验证
为验证流场计算方法的可靠性,将所用方法计算得到的车轮风阻系数与文献[7]中的实验结果进行比较.文献[7]中车轮直径为0.83 m,宽为2.5 m,车轮前进速度为9.592 m/s.计算时所采用车轮的尺寸与文献[7]的完全相同.
计算的静止和滚动车轮风阻系数与实验结果的对比如表1所示.
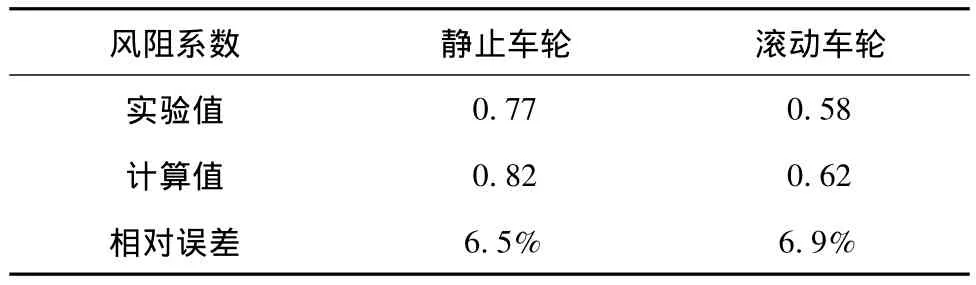
表1 车轮风阻系数计算值与实验值
由表1可看出,静止和滚动车轮的计算结果和实验结果的相对误差都在7%以内,因此认为所用的流场计算方法可靠.
3 计算结果及分析
根据原型轮辐周向一致性的特点,无论装在左轮还是右轮,车轮周围的流动状态以及同一编号的通风孔处的流动状态是完全相同的,所以车轮受到的风阻以及通过同一编号通风孔的通风量也是完全一样的.因此以下给出的原型结果,对左轮和右轮均适用.
车轮风阻系数CD为:
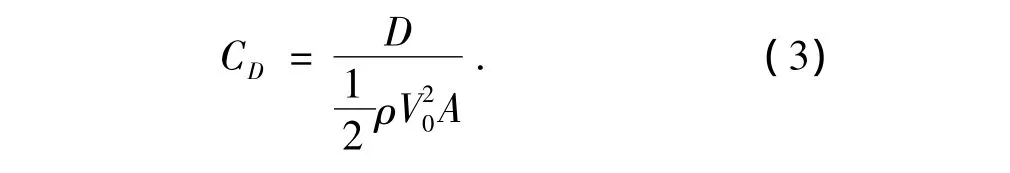
式中:D为车轮风阻;V0为车辆行驶速度;A为车轮z向正投影面积.
表2为原型和左轮改型及右轮改型的风阻系数.左轮改型风阻系数比原型增加了1.29%,右轮改型比原型增加了1.64%.说明改型的风阻系数均有所增加,但增加的很小.
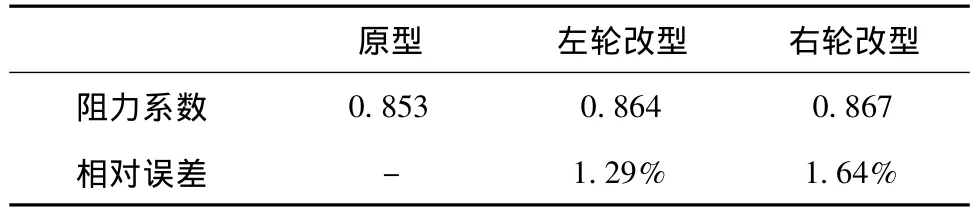
表2 风阻系数
表3和图6为通过原型、左轮改型和右轮改型10个通风孔的通风量以及总通风量.
由表3和图6可知,3种型式车轮的通风量随通风孔编号的变化情况都是先增大到最大值后减小,增加到第二个最大值后再减小.最大通风量都是通风孔4,第二大通风量都是通风孔8,较小通风量分别是通风孔1、6和10.
对比3种型式车轮同一编号通风孔的通风量可知,右轮改型的通风量最大,左轮改型的最小(通风孔2除外).因此右轮改型的总通风量最大,比原型增加了47.09%;左轮改型的最小,比原型减小了52.74%.说明改型轮辐只有装在右轮上才有利于提高通过通风孔的通风量.

表3 原型、左轮改型及右轮改型各通风孔的通风量 (m3·s)

图6 原型、左轮改型及右轮改型各通风孔的通风量
图7~图9为通过原型、左轮改型和右轮改型通风孔4中截面的速度矢量图和压强分布图.
通风孔4位于轮辐前部偏下的位置(见图2),而轮辐处于轮胎中间,前方来流绕过轮胎,才能作用到通风孔4,因此在车轮旋转以及绕过轮胎来流的共同作用下,原型车轮内部(右侧)大部分气流从下往上通过通风孔流出车轮.同时在通风孔上部由于受到高压的作用,气流在车轮外部(左侧)变为向下流动,见图7.
左轮改型由于其结构特点,即下部向里压凹,上部向外压凹(见图2),导致车轮内部的气流从上往下流出较易,外部的气流从下往上流入较易,因此内部大部分气流变为从上往下流出通风孔,外部部分气流从下往上流入通风孔,见图8.
右轮改型的结构正好与右轮改型相反,即下部向外压凹,上部向里压凹,导致车轮内部从下往上通过通风孔的气流更加容易流出.同时由于上部高压区的压强较原型的小些,流出通风孔的气流并不都是向下流动,在通风孔下部,小部分车轮外部的气流向上流入通风孔,见图9.
最终结果是右轮改型的通风量最大,原型次之,左轮改型最小.

图7 原型通风孔4
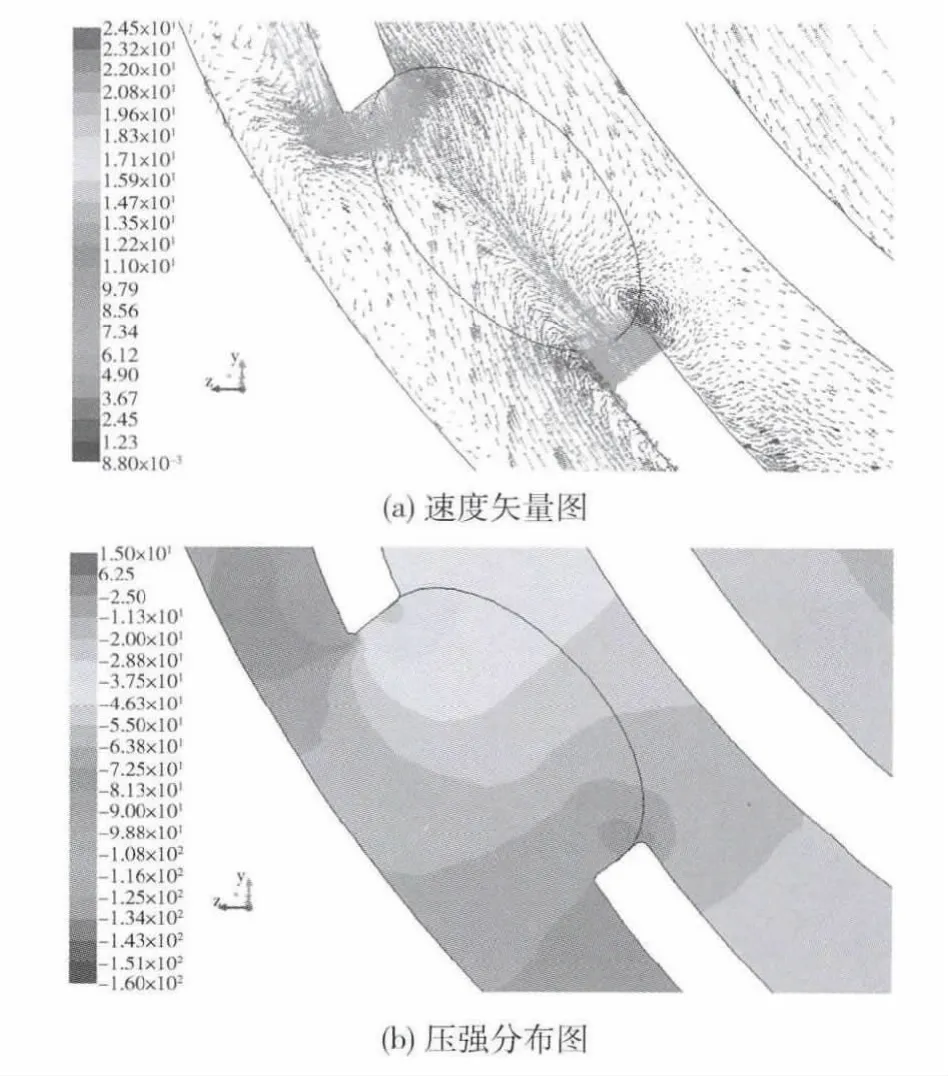
图8 左轮改型通风孔4

图9 右轮改型通风孔4
4 结论
左轮改型风阻系数比原型增加了1.29%,右轮改型增加了1.64%.说明改型的风阻系数均有所增加,但增加的很小.
3种型式车轮通风量随通风孔编号的变化情况都是先增大到最大值后减小,增加到第二个最大值后再减小.最大通风量都是通风孔4,第二大通风量都是通风孔8.
3种型式车轮同一编号通风孔的通风量,右轮改型的最大,左轮改型的最小(通风孔2除外).右轮改型的总通风量最大,较原型增加了47.09%,左轮改型的最小,减小了52.74%.说明右轮改型有利于提高通过通风孔的通风量.
[1]胡兴军,傅立敏,张世村,等.具有不同辐板车轮的空气动力学特性研究 [J].同济大学学报 (自然科学 版),2006,34(12):1684-1688.
[2]王国华.车轮空气减阻及其轮内传热 [D].长春:吉林大学汽车工程学院,2010
[3]芦克龙.基于CFD的汽车制动盘散热性数值计算与优化 [D].长沙:湖南大学机械与运载工程学院,2011
[4]谷正气,林肖辉,李伟平,等.车轮辐板形状对汽车气动阻力影响分析 [J].科技导报,2011,29(6):57-61.
[5]蒋建军.风冷降温式车轮开发与研究 [D].柳州:广西科技大学机械设计及理论,2013.
[6]Ryunosuke Kawashima1,Toshiaki Kanemo to.Automotive wheel with cooling fan for brake system and in-wheel motor[J].Journal of Mechanical Science and Technology,2013,27(6):1687-1692
[7]Axon Lee,Garry Kevin,Howell J.An Evaluation of CFD for Modeling the Flow around Stationary and Rotating Isolated Wheels[C].SAE Paper,980032.
