电传动履带车辆转向自适应控制策略仿真分析
2015-12-03盖江涛陈泳丹
刘 翼,盖江涛,陈泳丹,万 帆
(中国北方车辆研究所,北京 100072)
现代履带车辆的综合传动装置通常采用液压元件自适应调节驱动扭矩来克服转向阻力的,其转向稳定性较好,能抵抗较大程度的转向负载不确定性干扰[1-2].双侧电机驱动方案是电传动的基本方案之一,内外侧主动轮并无连接元件,转向过程的稳定性必须由整车针对电机的转向控制策略加以保证[3-4].
针对不同的电机控制指令,转向控制策略可分为控制电机转速和控制电机扭矩两种[5-6].采用转速策略时,驾驶员操纵信号解析为电机的目标转速.目前常用的控制方法是在电机控制器中,利用PID控制转速环,控制结果作为电机目标扭矩交由电流环响应.由于转速指令与目标驱动扭矩之间是一种非线性关系,利用PID算法精确解算扭矩值具有一定难度,也无法综合考虑两侧转速对转向阻力的耦合作用.实际转向时,转向阻力甚至可能非线性大幅突变,固定结构的PID不一定能实现转速闭环控制,车辆转向不一定稳定.采用扭矩策略时,目前常用的控制方法是将驾驶员操纵信号直接解析为电机的目标驱动扭矩.虽然电机的控制较为简单,但目标扭矩值算法过于简单,越野路况复杂及高速转向时也难以保证转向稳定.
本研究提出的自适应控制策略,是在转向控制器中利用参考系统以结合车辆动力学理论,利用自适应律进行变结构的转速闭环反馈控制,根据控制结果解算发送至电机的扭矩驱动指令.该策略能充分利用电机扭矩响应快速的优点,能保证转向快速稳定.
1 双侧电机驱动方案转向控制原理
双侧电机驱动方案采用两个独立的电机分别驱动内外侧主动轮,通过电机的调速,使两侧主动轮和履带产生速度差,从而使车辆完成转向.整车的驱动结构如图1所示.

图1 双侧电机驱动方案结构图
综合控制单元的功能是根据驾驶员的操作指令,依据转向控制策略计算出两侧电机控制器的控制指令.电机在电机控制器的作用下输出电磁扭矩,通过侧传动驱动主动轮来带动履带,使履带与地面之间产生作用力来驱动车辆完成转向.在大半径转向区,转向动力学模型为[7]:

式中:F1、F2分别为地面对车辆的驱动力和制动力;ρ为相对转向半径;ω为转向角速度;v为车辆行驶速度;m为整车质量;J为整车转动惯量;L为履带接地长;λ为转向中心纵向前移量;B为履带中心距;μmax为ρ=0.5时的转向阻力系数;φ为附着系数;f为行驶阻力系数;Mμ为转向阻力矩;N1、N2为内外侧履带的接地压力.
采用差速转向时,有效的控制策略应当使得v、ω能够跟随伺服于驾驶员的期望指令v*、ω*.v的伺服由(F1+F2)实现,控制相对简单,与直驶时类似;ω的伺服由(F2-F1)实现,控制则较为困难,因为Mμ是非线性和突变的.
2 自适应控制律设计
为设计合理的自适应控制律,将ω由ω1至ω2的全局调速过程,分解为无穷段极小邻域W(ω0;δ)={ω:ω ∈[ω1,ω2],|ω -ω0| <δ,δ→0+}内的调速过程.只要自适应律能够实现每个W(ω0;δ)内的ω伺服,那么,当ω0遍历区间[ω1,ω2]时,全局ω伺服即随之实现.
2.1 系统等效线性化
在邻域W(ω0;δ)内将Mμ中关于状态ω的非线性项 β(ω)=(0.925+0.15ρ)-1线性化,斜率取为˙β(ω0),幅值仍保持为β(ω0),则角速度状态方程线性化为:

显然有 a>0,u'>0.
为便于叙述,将u'的计算公式记作φ(μmax,f,λ);a的计算公式记作ξ(μmax,f,λ),括号内的参数代表针对路面情况选用的计算参数.
由于保证了˙β(ω0)及˙ω(ω0)不变,因此W(ω0;δ)内的线性方程与原系统方程等效.虽然算法φ能够获得线性系统的等效输入,但由于系统参数是时变的,并且实际转向时地面参数是未知的,因此不能直接设计等效系统的闭环极点,但可以采用模型参考的方法进行自适应控制.
2.2 控制律设计
模型参考自适应控制的基本结构包括参考系统和实际系统两个被控对象,基本原理是通过控制结构参数的自适应变化,使得实际系统的输出能够跟随参考系统.在转向控制中,参考系统sys_m具有预定的转向阻力系数μm、行驶阻力系数fm、质心前移量 λm.它针对输入的理想牵引力 F1*、F2*,产生理想的参考输出:车速vm和转向角速度ωm.车辆实际系统sys_p相应地具有参数 μp、fp、λp,实际输入牵引力F1、F2和实际输出车速vp、转向角速度ωp.
自适应控制策略的基本算法为:通过自适应律的调节作用,完成ωp闭环的变结构参数控制,将理想牵引力修正为适当的实际牵引力,使得ωm与ωp的偏差e能够迅速收敛.
以φ(μm,fm,λm)对参考系统和实际系统的ω状态方程做线性化,得到W(ω0;δ)内的系统状态方程:

显然在相同的等效输入r下,e不可能为0,因此自适应算法的核心是如何将实际系统的输入r校正为u,从而保证误差收敛.u的算法设计为:
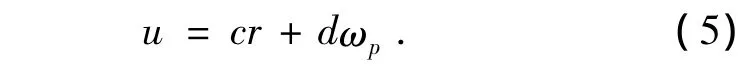
参数c、d的自适应控制律设计为:
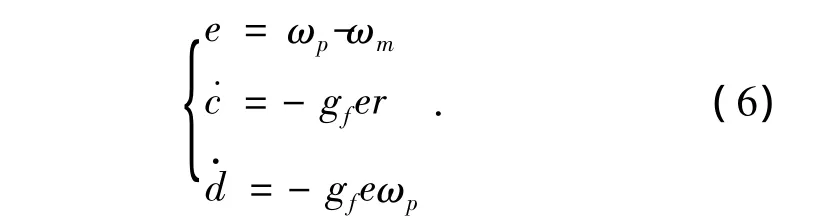
式中:gf是反馈系数,且gf>0.
输入r作用于参考系统,输入u作用于实际系统,控制的结果是e收敛于零,实现ωp对ωm的伺服.
2.3 系统稳定性证明
引入标称参数c*、d*及误差参数φc、φd:
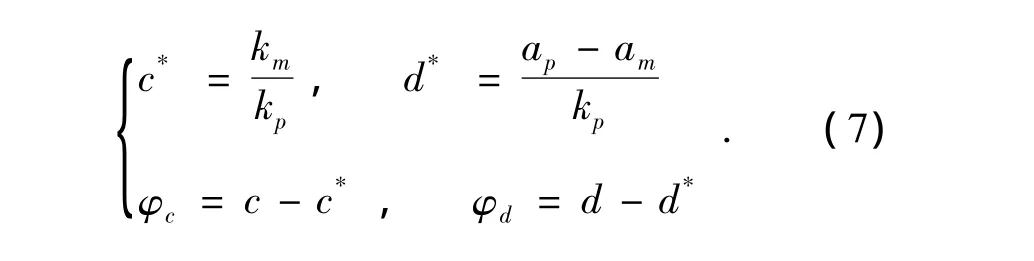
由于参考系统可以自行设计,可取恒定不变的μm、fm、λm,使得ωm有界且响应快速稳定,因此讨论稳定性时,只需要考虑ωp、c、d三个状态变量.系统的Lyapunov函数可以选取为
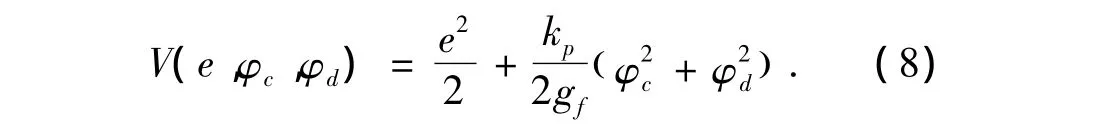
其导数值为

因此自适应控制系统稳定,且e有界.
gf只需为正值即可满足稳定性要求,其值越大e收敛速度越快;但gf特别大且路面参数变化很快时,ωp容易产生振荡.实际控制时,要结合路况选取gf.同时,c和d的反馈系数可以取为不同,由于ωp的数量级低于r,因此d的反馈系数取值应大于c的反馈系数.
3 自适应控制结构
根据前述分析,转向控制结构应如图2所示,主要包含参考系统sys_m、实际系统sys_p两个被控对象,以及目标牵引力算法F、等效输入算法φ、自适应反馈算法c和d.
控制的基本原理是:通过合理地设计F,使得参考系统的响应vm、ωm快速稳定,且能够跟随操纵指令解释而来的期望响应v*、ω*;通过有效的自适应控制,使得实际系统的响应vp、ωp跟随vm、ωm,从而使车辆完成期望的稳定的转向.
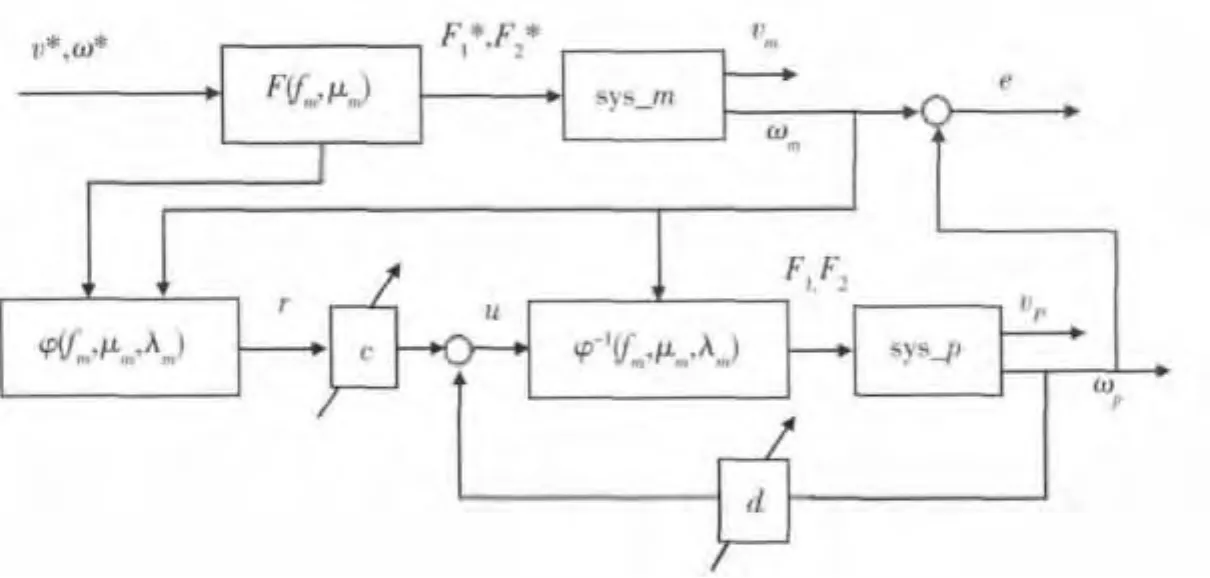
图2 转向自适应控制结构
参考系统的数学模型设计为恒定参数(μm,fm,0)下按式(1)表达的状态方程,为简便λm可取为0.算法F的计算方程相应为:

算法φ的作用是根据F1*、F2*求取用于自适应控制的等效输入r,通过自适应的变结构参数c、d,产生实际系统的新等效输入 u,再根据φ-1与˙v=0获得作用于实际系统的目标牵引力F1、F2,算法可由式(10)类比.
4 仿真结果及分析
针对某型履带车辆,做了仿真试验.仿真模型如图3所示.其中,实际系统可用参数(μp、fp、λp)按式(1)表达的状态方程来进行描述.其中,电机的目标扭矩将根据两侧传动比,由F1、F2方便解出.电机按其理想外特性进行扭矩限幅,可等效为扭矩响应一阶惯性系统.实际系统的输出vp、ωp代表整个控制系统得到的控制结果,理想的控制策略将使得vp、ωp能够跟随v*、ω*.

图3 转向自适应控制仿真模型
仿真的关键在于使参考系统与实际系统的路面参数有较大差异,且实际系统的参数突变剧烈,以模拟实际控制时的路面与未知转向阻力变化情况.
4.1 考虑驱动能力约束的工况
这部分仿真中考虑了电机的极限驱动能力,以及地面的附着系数的影响.参考系统的参数统一取为μm=0.8,fm=0.06,λm=0;实际系统的仿真参数按下面选取:

其中rand函数代表每隔0.2 s产生的[-1,1]内的随机数,在Simulink仿真中用Uniform Random Number模块实现.
自适应控制律中,c和d的积分初值取为0,gf取定为500.
设定3种较为接近履带车辆极限转向能力的差速转向工况进行仿真,参数见表1.

表1 三种差速转向工况参数
3种工况的转向角速度阶跃响应如图4所示,虚线表示期望响应.
结果表明:自适应控制策略下的角速度阶跃响应快速,没有超调,响应稳定,能够较好地跟随期望角速度,车辆的转向稳定性能良好.

图4 转向角速度响应
3种工况的车辆行进速度响应如图5所示.
结果表明:自适应控制策略下,车辆的行进速度能够保持不变,从而保证车辆完成差速转向.须指出的是,差速转向只是履带车辆的一种基本转向方式,如果希望实现升速或者降速转向,只需要按照ω的自适应控制方法,对v加以类似控制即可.
3种工况的相对转向半径响应如图6所示,虚线表示期望响应.
结果表明:自适应控制策略下,车辆能够迅速实现期望的相对转向半径,且在路面阻力高频高幅突变下仍然能够保证半径的稳定伺服.这表明驾驶员能够较简易地操纵车辆,使其稳定地跟随期望的转向轨迹,车辆的转向十分稳定且可控.
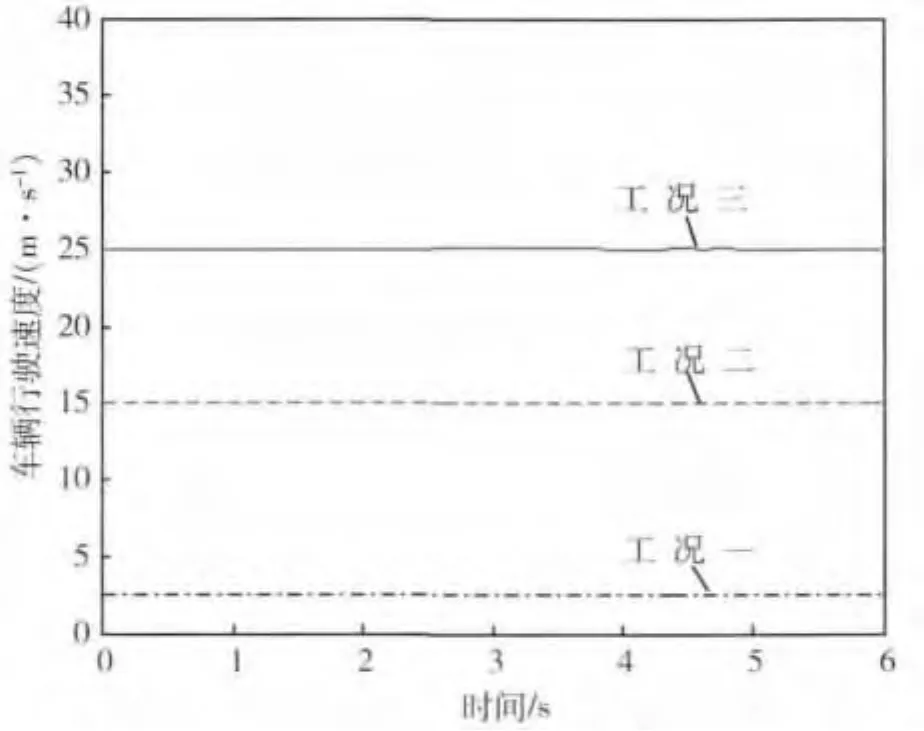
图5 车辆行驶速度响应
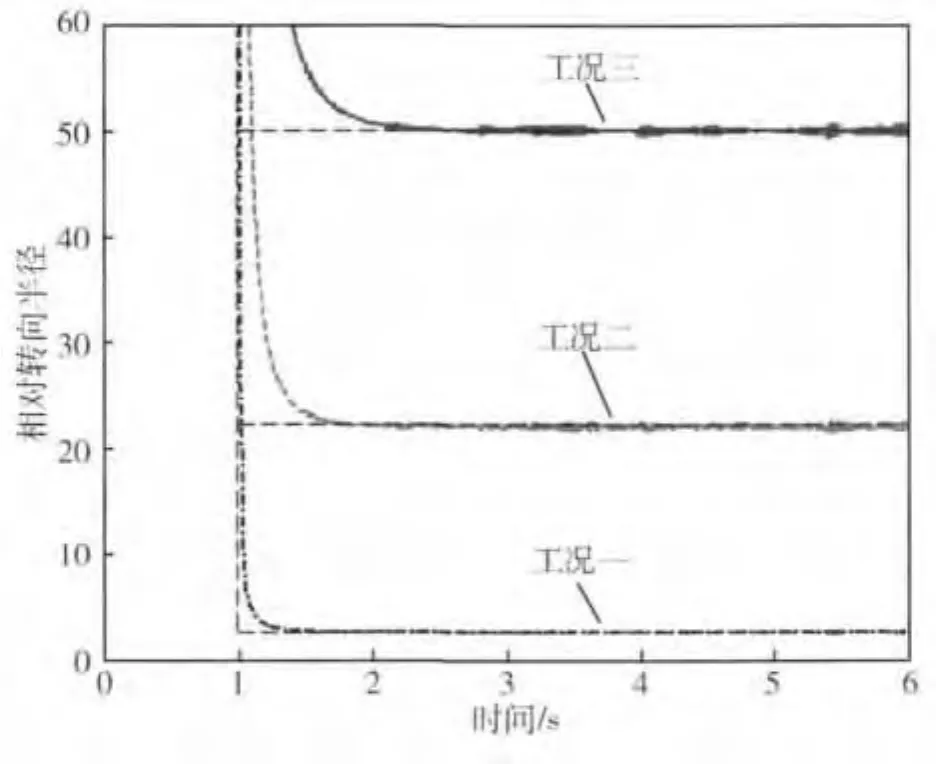
图6 相对转向半径响应
4.2 不考虑驱动能力约束的工况
不考虑电机最大扭矩以及地面附着系数的限制,进行3种差速转向工况仿真,以单纯地从数学的角度验证控制策略的有效性.设定的工况都是高速转向,且μp与μm相差很远,具体参数说明见表2.
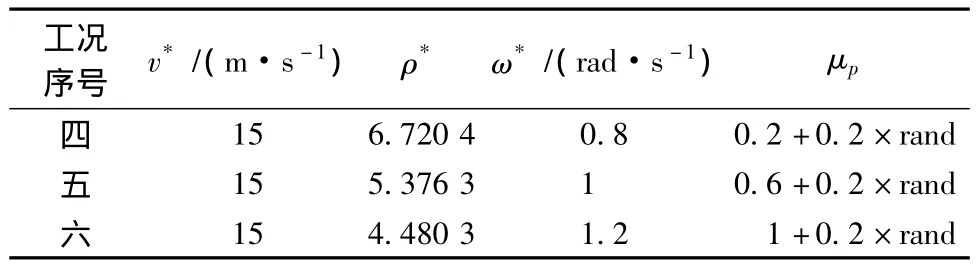
表2 3种差速转向工况参数
剩余的参考系统、自适应律、电机延时参数等,皆与工况一相同.仿真结果表明,3种工况的车速都能维持15 m/s不变,此处不再作图表示.转向角速度阶跃响应如图7所示,虚线表示期望响应.
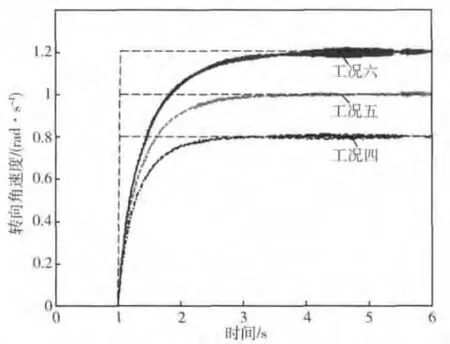
图7 车辆转向角速度响应
结果表明:参考系统并不需要根据实际路面来预估μm,只需将其取定为0.8,就能够实现多种路面条件下的转向稳定性控制.控制系统对转向阻力变化的适应性较好.
在工况一和工况六中,ωp出现了抖振,这是由于选取了较大的gf以加快e收敛.抖振虽然不影响控制系统的稳定性,但可能会激发系统的未建模特性,产生不可预知的影响,因此需要消除或削弱抖振.由于式(6)设计的控制律只需gf大于0就能保证控制系统稳定,因此可采用变参数的方法,例如将gf设计为分段函数:

5 结论
1)对转向动力学模型的等效线性化具有一定可行性,其决定的等效输入能够应用于双侧电机驱动履带车辆的自适应控制策略,能够保证控制系统的稳定性、鲁棒性和收敛性.
2)提出了双侧电机驱动履带车辆转向负载自适应控制策略,通过仿真分析,表明在转向阻力高频高幅变化的工况下,该策略仍然能很好地保证履带车辆实现期望的转向调速过程,保证任意大半径转向工况下的转向稳定性.
3)自适应控制策略将转速闭环设置于整车控制器中,电机只需响应扭矩,降低了电机控制器的设计难度,同时有效地利用了电机扭矩响应快速准确的特点.
[1]李宏才,闫清东,韩立金.履带车辆转向功率机械回流的差速机构研究 [J].机械设计与研究,2010,26(4):65-70.
[2]程军伟,高连华,王红岩,等.履带车辆转向分析[J].兵工学报,2007,28(9):1110-1115.
[3]臧克茂,廖自力,李 华.坦克装甲车辆电传动总体技术的研究 [J].车辆与动力技术,2007,(1):5-12.
[4]邹 渊,张承宁,孙逢春,等.电传动履带车辆双侧驱动控制研究 [J].北京理工大学学报,2007,27(11):956-959.
[5]李 波,张承宁,李军求.基于 RecurDyn和Simulink的电传动车辆转矩控制策略 [J].农业机械学报,2009,40(7):1-5.
[6]翟 丽,孙逢春,谷中丽,等.电传动履带车辆电子差速转向控制策略 [J].北京理工大学学报,2009,29(2):113-117.
[7]刘国民,黄海东,张 萃.履带底盘转向解析[J].中国工程机械学报,2010,8(3):309-313.
