地铁运行引起地面局部振动放大现象的数值分析

张啟乐，刘林芽，李纪阳

（华东交通大学 铁路环境振动与噪声教育部工程研究中心，南昌 330013）

地铁运行引起地面局部振动放大现象的数值分析

张啟乐，刘林芽，李纪阳

（华东交通大学 铁路环境振动与噪声教育部工程研究中心，南昌 330013）

；以南昌地铁一号线穿越的土层为研究对象，建立轨道—隧道—大地的三维有限元模型，施加粘弹性人工边界，从隧道埋深，场地土层弹性模量等角度分析了由地铁运行所诱发的地面振动的传播规律。研究表明：地面振动的衰减并不是随着与隧道中心距离的增加呈严格意义单调递减，而是距离线路某一范围内存在一个振动放大区。隧道埋深越深，振动放大区出现在距离隧道越远的位置，而且振动放大区出现的次数会增加；土层越硬振动放大区越靠近隧道，振动放大区出现的次数会越多。振动放大区第一次出现在距离隧道约20 m～30 m处，振动反弹量比较大，被放大频率带主要分布在6 Hz～28 Hz，其中8 Hz～12 Hz最为集中，如果侵入建筑群，需特别关注。第二次第三次振动反弹量小，重视程度可以放宽。

振动与波；地铁；有限元模型；振动放大区；隧道埋深；土层弹性模量

地铁交通方便出行的同时引起的环境振动污染问题也日趋突出，越来越受到有关部门和工程界的高度重视[1]。刘维宁等建立隧道结构-地层空间有限元模型，发现离开地铁隧道中心线一定距离的地表范围内，存在两个振动放大区，并指出这个距离依地层条件和隧道埋深而定[2]。闫维明，聂晗等对某地铁1号线沿线典型区段地铁引起的地面进行现场测试，实测表明，地下铁道列车运行引发的地面振动的衰减规律不是随着与线路距离的增加呈单调递减，而是在离地铁线路某一距离有一振动放大区[3]。马蒙等利用地表落锤试验和半空间位移格林函数解析解，发现地表体波和瑞利波衰减速度不同引起轨道交通地表振动局部放大现象成因[4]。由于振动放大现象成因的复杂性，大多数文献只是给出了定性的结论，没有关于振动放大区出现的距离与地质条件，隧道埋深等因素关系的定量表述。本文通过建立三维轨道—隧道—大地有限元模型，从数值计算的角度，给出影响振动放大区出现的定量描述，以期为地铁工程减振措施的设计，为地铁线路附近新建建筑隔振措施的选择提供参考。

1 有限元模型

1.1 单元类型的选择

在建立轨道—隧道—大地有限元模型时，忽略土体的非线性应变和塑性变形，将土层简化为各向同性的线弹性体，用SOLID 45单元模拟土体，SOLID 45单元用于构造三维实体结构，单元通过8个节点来定义，每个节点有3个沿着xyz方向平移的自由度。钢轨用梁单元BEAM 188模拟，BEAM 188是一个二节点的三维线性梁，基于Timoshenko梁理论，具有扭切变形效果，适用于分析细长的梁，在每个节点上有6个或7个自由度[5]。轨道板和隧道衬砌按壳体SHELL 163单元考虑，衬砌厚度取0.3 m；弹性扣件和CA砂浆考虑其刚度与阻尼，用弹簧COMBINE 14单元模拟，COMBIN 14具有1维，2维或3维应用中的轴向或扭转的性能。扣件间距按实际情况考虑，取0.625 m。本文计算模型尺寸沿轨道延伸方向取100 m，垂直于轨道延伸方向取100 m，竖向取50 m，模型包括上行线和下行线两个隧道，如图1—图2所示。把地铁列车对轨道的竖向轮轨作用力简化为移动的轴荷载，两个隧道内的列车相向行驶，在计算域边界上施加局部粘弹性动力人工边界单元，防止在边界上发生波的反射造成计算结果失真[6]。

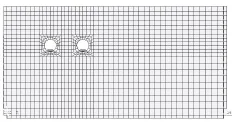
图1 三维大地有限元模型

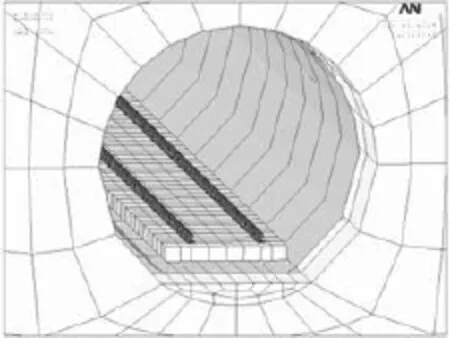
图2 大地模型隧道部分详图

1.2 材料参数的确定

本文涉及的大地土层参数均来自南昌轨道交通集团提供的“南昌市轨道交通1号线一期工程B合同段中山路站—八一广场站区间岩土工程详细勘察报告”。报告对拟建场地的地基岩土的地质年代、成因类型、地层结构与分布规律等作了详细的评价，在此只列出有限元模型中所需的岩土参数，见表1，隧道内部各混凝土结构，钢轨以及扣件等弹性模量很大，在计算时假设应变较小，所有材料始终均处于线弹性状态，具体参数如表2所示。

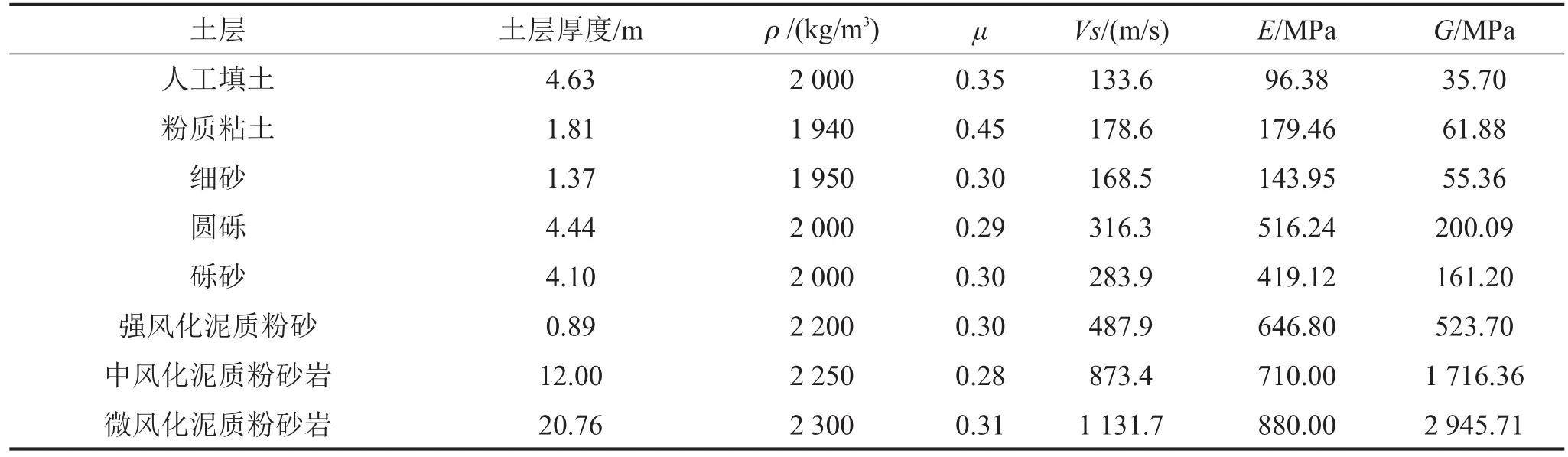
表1 岩土参数

1.3 动力方程阻尼的确定

有阻尼作用的连续弹性介质，经有限元离散为多自由度体系后，整体的动力平衡方程为[8]

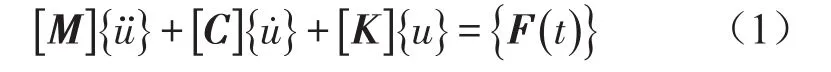
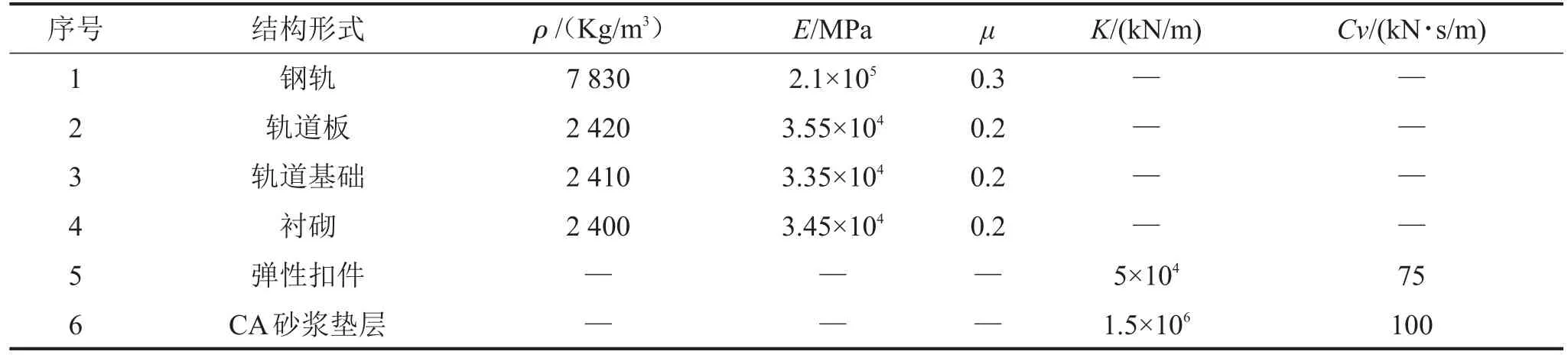
表2 隧道中各结构形式材料参数[7]

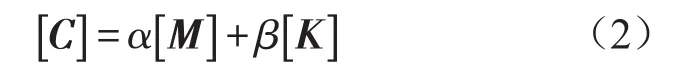
式中α为粘性阻尼分量，β为滞后或固体或刚度阻尼分量。

根据振型正交条件，待定系数α和β与振型阻尼比之间应满足关系

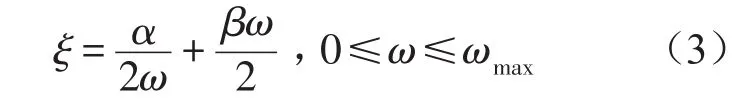
取两个振型固有频率ωi和ωj，与其对应的振型阻尼比为ξi和ξj，分别将其代入公式（4）和公式（5）并求解所得到的方程组，可得到公式中的Rayleigh阻尼系数α和β。

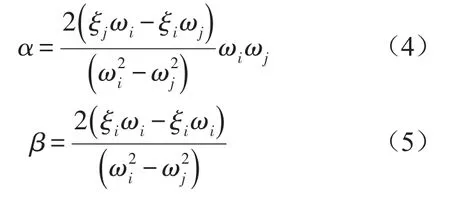
对系统进行模态分析可求出2个固有频率ωi和ωj，并可以通过实验或者类似的相关工程的资料可知道2个阻尼比ξi和ξj，由式可求得阻尼比系数α和β。α阻尼与圆频率成反比，此时高振型的阻尼很小；β阻尼与圆频率成正比，高振型的阻尼比将非常大，这相当于加大了高振型的衰减。

系统阻尼比本文采用经验数据[9]：岩土结构整体系统的阻尼比对较硬土取0.06～0.08；对中软土取0.08～0.1；对较软土取0.1～0.12。土层类型的划分参照《建筑抗震设计规范GB 50011一2001》[10]的规定：软弱土，vs＜140 m/s；中软土，140 m/s＜vs＜250 m/s；中硬土，250 m/s＜vs＜500 m/s。vs为土层的剪切波速。南昌土层中软土为主，故取系统阻尼比ξi=ξj=0.08；对系统进行模态分析取前两阶频率带入公式，解的α=2.27，β=2.4×10-4。作振型阻尼比与频率的关系如图3所示。

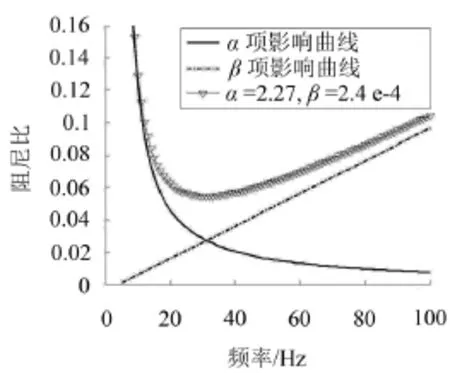
图3 振型阻尼比与自振频率的关系

从图3可以看出，阻尼落在0.06～0.12之间，所以认为当阻尼系数α=2.27，β=2.4×10-4时能很好解决南昌地区土层瞬态分析的系统阻尼问题。

2 计算结果

2.1 隧道埋深对振动响应沿地面衰减规律的影响

为适应地铁沿线土质的变化，地铁隧道埋深往往设计成变化的，研究不同埋深影响下地面振动的衰减规律可以对以后地铁线路设计提供参考和建议。在ANSYS模型中只改变隧道埋深，即分别设为0 m(轨道在地面)，5 m，10 m，15 m，20 m，25 m共6种工况而不改变其他参数。作隧道埋深的变化与振动响应衰减的关系图，如图4—图6。

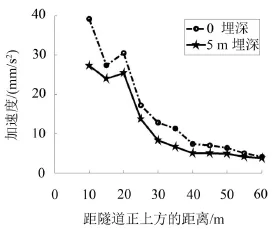
图4 埋深0和5 m振动响应随距离衰减

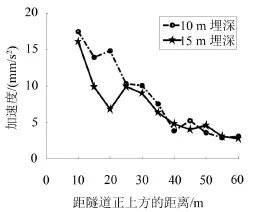
图5 埋深10 m和15 m振动响应随距离衰减

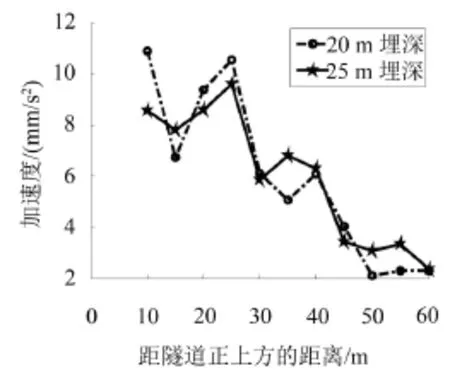
图6 埋深20 m和25 m振动响应随距离衰减

由图4—图6可以看出，振动加速度随着与隧道中心距离的增大呈逐渐减小的趋势，而且距离越远振动加速度衰减的速度越慢，但不是严格意义上的单调衰减，在衰减过程中局部有反弹现象。

由图4可知，隧道埋深0 m和5 m时，振动放大区出现在距离隧道中心正上方约20 m处，且只出现一次。隧道埋深10 m时在距离隧道中心正上方约20 m处出现振动放大效应，并在45 m左右位置处振动加速度又出现少许的回升。隧道埋深为15 m时，振动加速度第一次反弹出现在25 m左右，第二次少许回升在50 m左右处。当隧道埋深20 m和25 m时，加速度分别在距离25 m和35 m～40 m左右出现振动放大效应，甚至在55 m～60 m处出现第三次轻微量反弹。

由此可以发现，振动放大效应与隧道埋深有密切的关系。隧道埋深越浅，振动放大区出现的位置距离隧道越近；隧道埋深越深，振动放大区出现的位置离隧道中心越远，而且振动放大区出现的次数会增加。特别指出，距离隧道20 m～30 m往往是商铺或者居民建筑分布区，这个位置恰好是振动响应第一次放大区，极易造成建筑振动的超出环境振动标准，故有关部门应该格外重视。第二次和第三次振动反弹时，因为振动本身已经衰减到很小，而且反弹量不大，在此位置的建筑振动超出限值的可能性不大，所以重视程度可以适当放宽。

2.2 土质不同对振动放大区的影响

弹性模量是土层最重要的地质条件参数之一，土层的弹性模量侧面体现土的软硬程度。研究不同土质下振动响应的衰减，能够针对不同地区的减振措施的设计提供参考。在ANSYS模型中只改变土层弹性模量，分别为95 Mpa，165 Mpa，235 Mpa，305 Mpa，375 Mpa，445 Mpa共6种工况，隧道埋深固定为15 m，作土层弹性模量与地面振动响应关系如图7—图9所示。

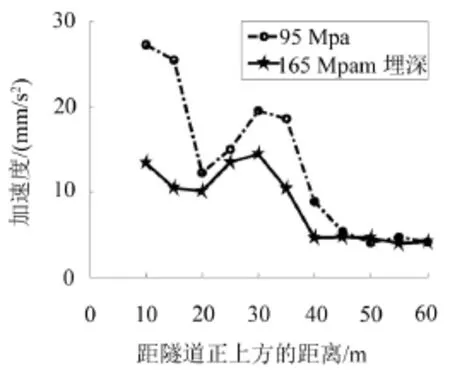
图7 弹性模量95 Mpa和165 Mpa振动响应随距离衰减

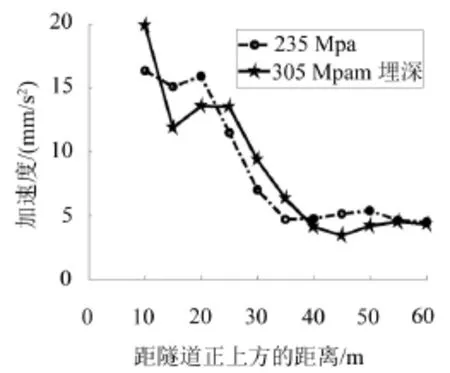
图8 弹性模量235 Mpa和305 Mpa振动响应随距离衰减

从上图7—图9可知，无论何种土层振动响应均随着与隧道距离的增大而大致呈减小的趋势。距离隧道越远，衰减越慢。

土层弹性模量为95 Mpa和165 Mpa时，两种工况的衰减规律近似，在距离隧道约20 m～40 m处出现振动反弹，但90 Mpa的振动响应近乎始终要大于165 Mpa。土层弹性模量为235 Mpa和305 Mpa时，振动加速度在20 m～30 m位置出现首次反弹，在距离隧道50 m左右位置不降反增，出现第二次少许的反弹，但是反弹量不大。当弹性模量为375 Mpa时，第一次振动放大的位置在20 m处，第二次在40 m左右的位置，较前面95 Mpa，165 Mpa，235 Mpa，305 Mpa四种工况第二次反弹的位置均有提前，即向隧道中心的位置靠近。当土层弹性模量为445 Ma时，振动响应在衰减过程中，距离隧道约15 m处首先出现反弹，然后分别大约在40 m和55 m出现两次微量反弹，反弹量不大。

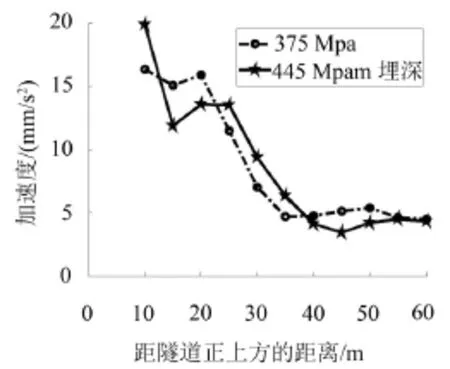
图9 弹性模量375 Mpa和445 Mpa振动响应随距离衰减

由此可知，土层越软，振动放大区出现的位置越远离隧道，土层越硬振动放大区越靠近隧道，而且土层越硬，振动放大区出现的次数有增多的趋势。振动反弹第一次出现的位置，依不同的土质条件而不同，大约在10 m～40 m范围内，这个范围内的敏感建筑需要采取隔振或者加固措施。第二次第三次振动放大区一般出现在50 m之外，振动响应已经衰减到很小，加之反弹量不大，故可以忽略。

2.3 振动放大区放大的频率成分分析

振动在衰减过程中有局部放大现象，研究振动放大区的被放大的响应的频率成分，可以在振动敏感区有针对性选择隔振元件，避免发生共振。

由前面计算可知地铁运行引起的振动放大区主要集中在20 m～30 m范围内，所以在此只选取20 m～30 m范围内的振动响应衰减过程的传递函数的频率成分进行分析。南昌地铁一号线埋深多分布在15 m～17 m之间，在此只给出埋深条件为15 m的工况。

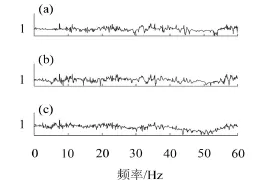
图10 (a)R=20 m相对于R=15的传递函数 (b)R=25 m相对于R=15的传递函数 (c)R=30 m相对于R=15的传递函数

R为选取的振动响应点与隧道正上方的距离。由图10可以看出，振动响应在随着与隧道的距离增大而衰减的过程中，高频振动和低频振动都有所衰减，但是高频振动要比低频振动衰减的速度要快。在R=25 m时，振动响应明显增大，被放大的频率主要分布在6 Hz～28 Hz，其中8 Hz～12 Hz被放大的现象最为明显。这一计算结果与闫维明，聂晗等对某地铁1号线沿线典型区段地铁引起的地面振动特性及其传播规律分析结果[3]一致。为减轻地铁运行引起的环境振动的影响，在振动放大区新建建筑物时有必要采取隔振措施，但采用的隔振元件的固有频率一定要远离这个范围，以免发生共振。

3 结语

在轨道—隧道—大地有限元模型中通过控制隧道埋深和土层的弹性模量等变量，分析不同工况下地面振动响应的衰减可以得到以下规律：

(1)隧道埋深越深，振动放大区出现的位置有离隧道中心越远的趋势，而且埋深越深，振动放大区出现的次数会增加。当距离隧道中心比较远时，振动反弹量很小，可以忽略。第一次振动放大区距离隧道约20m～30m，往往是商铺或者居民建筑分布区，应该格外重视。

(2)土层越软，振动放大区出现的位置越远离隧道，土层越硬振动放大区越靠近隧道，而且土层越硬，振动放大区出现的次数有增多的趋势。第二次第三次振动放大区一般出现在50 m之外，振动响应已经衰减到很小，加之反弹量不大，故可以忽略。

(3)振动在随距离增大而衰减的过程中，高频振动要比低频振动衰减的速度要快，在振动放大区被放大的频率主要分布在6 Hz～28 Hz，其中8 Hz～12 Hz更为集中，如果在这个位置采取隔振措施时，隔振元件的固有频率一定要远离这个范围。

[1]雷晓燕，圣小珍.铁路交通噪声与振动[M].北京：科学出版社，2004.

[2]刘维宁，夏禾.地铁列车振动的环境影响[J].岩石力学与工程学报，1996，15(10)：586-593.

[3]闫维明，聂晗每，任珉.地铁交通引起地面振动的实测与分析[J].铁道科学与工程学报，2006，03(02)：1-5.

[4]马蒙，刘维宁，王文斌.轨道交通地表振动局部放大现象成因分析[J].工程力学，2013，30(4)：275-309.

[5]王新敏.ANSYS工程结构数值分析[M].北京：人民交通出版社，2007.

[6]刘晶波，王振宇，杜修力，等.波动问题中的三维时域粘弹性人工边界[J].工程力学，2005，22(6)：46-51.

[7]蒋崇达.内置式钢弹簧浮置板轨道动力特性分析[D].南昌：华东交通大学，2013.

[8]马宏伟，吴斌.弹性动力学及其数值方法[M].北京：中国建材出版社，2000.

[9]杨小卫.桩—土—结构动力相互作用的数值分析[D].武汉：武汉理工大学，2005.

[10]GB 50011-2001建筑抗震设计规范[S].中华人民共和国国家标准.

NumericalAnalysis of Ground VibrationAmplification Phenomenon Caused by Subway Operation

ZHANG Qi-le,LIU Lin-ya,LI Ji-yang
（Engineering Research Center of Railway Environment Vibration and Noise,Ministry of Education, East China Jiaotong University,Nanchang 330013,China）

Taking the soil stratum of Nanchang No.1 subway as the research object,the rail-tunnel-soil coupled 3D finite element model was established,and the artificial cohesive elastic boundary condition was applied.The propagation law of ground vibration induced by the subway operation was analyzed in the aspects of the depth of the tunnel and the elastic modulus of the soil stratum.The research shows that the ground vibration does not attenuate monotonically with the increasing of the distance from the subway,but there exist several vibration amplification regions somewhere else.With the increasing of the depth of the tunnel,the amplification regions go farther away from the tunnel and their number increases.With the increasing of the elastic modulus of the soil stratum,the amplification regions go closer to the tunnel and their number also increases.The nearest vibration amplification region,referred to as the first amplification region,is about 20 m-30 m away from the tunnel,and the vibration bounce is large there.Amplification frequency bands are distributed in the 6 Hz-28 Hz range,and mainly concentrated in 8 Hz-12 Hz.One should pay special attention to the first amplification region if it invades nearby building areas.However,the second and third amplification regions can be ignored since they have only small vibration bounces.

vibration and wave;subway;finite element model;vibration amplification;buried depth of tunnel;elastic modulus of soil stratum

TB533+.2

A

10.3969/j.issn.1006-1335.2015.02.027

1006-1355(2015)02-0116-05

2014－08－24

列车低噪声车轮声辐射优化模型及其遗传算法研究（51268014）；江西省高等学校科技落地计划项目（2024）

张啟乐（1988－），男，山东潍坊人，硕士研究生，主要研究方向：轨道交通振动与噪声。

刘林芽（1973－），男，教授，博士生导师。E-mail:18146701025@qq.com