大型岸桥地震反应分析中阻尼模型的讨论

李 哲，王贡献，胡吉全，王 东

（武汉理工大学 物流工程学院，武汉 430063）

大型岸桥地震反应分析中阻尼模型的讨论

李 哲，王贡献，胡吉全，王 东

（武汉理工大学 物流工程学院，武汉 430063）

以现有的条件无法对大型结构进行地震试验，只能采取缩比模型试验配合有限元时程分析。以某岸桥结构为例，进行时程数值计算时阻尼模型在很大程度上影响计算的精度。采用工程上最常用的4种不同Rayleigh阻尼模型对岸桥1：15缩比模型进行了时程动力分析，并同振动台地震模拟试验所得的试验值进行了比较，选出与试验结果最相近的阻尼模型。将该阻尼模型用在岸桥原型的动力时程分析中，将所得结果进行相似系数变换后，与缩比模型试验结果进行比较。结果显示岸桥原型采用该阻尼模型进行动力时程分析与试验之间的误差在许可范围之内，说明采用该阻尼模型是正确的，同时也验证了缩比模型的可靠性。

振动与波；阻尼模型；时程分析；岸桥结构；振动台试验；缩比模型

为满足现代化港口需要而制造的大型集装箱起重机（岸桥），因其结构的特殊性，在地震灾害中最易遭受破坏。明确岸桥结构地震载荷作用下的破坏模式及破坏机理，提高其抗震性能，是当前安全生产和设计领域高度关注的问题[1]。

岸桥结构庞大，目前的条件无法对实际结构进行抗震试验。采用有限元数值模拟配合缩比模型试验可以得到较好的结果。有限元时程分析中，不同阻尼模型对结构地震反应的影响是不可忽略的[2]。由于缺乏具有说服力的试验验证，在有限元时程分析中选用哪一种阻尼形式比较合理，尚没有一个评价指标。文献[3]中设计出1:50的岸桥缩尺模型，采用有限元软件对岸桥模型进行仿真分析，并进行模型试验，试验值与仿真结果有较高的相似度。文献[4，5]基于动力相似理论建造了一个相似比为1: 20的岸桥缩尺模型，在此基础之上他们进行了一系列的仿真分析和振动台地震试验并取得较好的结果。上述文献中都没有对仿真分析中采用的阻尼模型进行说明，更没有用试验来验证时程分析中所取阻尼模型是否可靠。

结构地震反应时程分析中，最广泛采用的阻尼模型是Rayleigh阻尼模型[6]。Rayleigh阻尼系数在很大程度上影响分析结果，合理选取Rayleigh阻尼系数对评价岸桥的动力特性十分重要。采用工程上最常用的4种Rayleigh阻尼系数，对同一岸桥结构缩比模型进行动力时程分析，比较不同阻尼系数下的结构地震响应，并与振动台地震模拟试验所得的试验值进行了比较，选出与试验结果最相近的阻尼模型。将该阻尼模型用在岸桥原型的动力时程分析中，并与缩比模型试验结果进行比较。为岸桥结构地震反应研究选用合理的阻尼模型提供参考。

1 阻尼模型

振型阻尼比随固有频率的变化与试验数据基本一致，使得Rayleigh阻尼成为应用最为广泛的阻尼模型

式中C为阻尼矩阵，M、K为质量和刚度矩阵，α、β为比例常数，可以分别根据给定的第m阶振型阻尼比ξm、固有频率ωm和第n阶振型阻尼比ξn、固有频率ωn确定

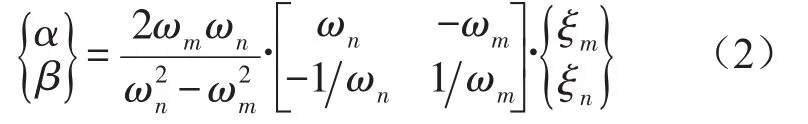
振型阻尼比可通过试验获取，低阶振型在一般工程结构的动力反应中起主导作用，通常取低阶振型来确定比例常数α和β，例如前两阶振型的频率和阻尼比，其他各阶振型的阻尼比可通过下式求解

目前，结构动力反应计算中瑞利阻尼系数的4种确定方法：

（1）假定组成Rayleigh阻尼质量矩阵和刚度矩阵对阻尼贡献相等，比例常数α和β可以表示为

由结构的基频ω1，得到阻尼系数α和β。

（2）假如选定结构的敏感频率范围为 fa～ fb，在频率边界ωa，ωb处的阻尼比可用下式表达

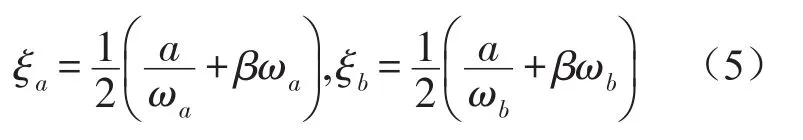
根据式（5）求出α和β。

（3）以方法（2）为基础，吉田望等学者对其进行了改进[7]，令

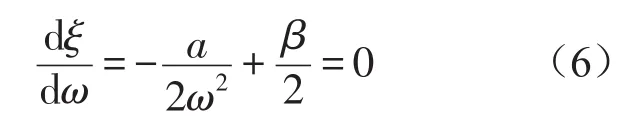
（4）Idriss等[8]基于方法（1）进行了适当的改进，确定了新的瑞利阻尼系数取值方法，用ω1和ω2两个频率来确定α和β，ω1为结构的基频，ω2=nω1， n是大于的奇数，其中ωe为地震波的主频。此法既考虑结构频率特性，也考虑地震动频率特性。

2 岸桥缩比模型地震反应

2.1 研究对象与模型

通过对相似比为1：15的集装箱岸桥缩比模型进行地震反应计算分析比较，讨论不同阻尼模型对岸桥结构地震反应的影响。岸桥主要由门架结构（主要包括海陆侧立柱、海陆侧上横梁、海陆侧下横梁及门框横梁）、前后大梁、前后拉杆等组成，如图1所示。岸桥金属结构材料取为Q 345钢，弹性模量206 GPa，泊松比0.3，密度7 850 kg/m3。

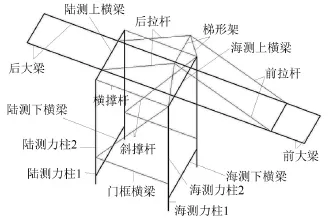
图1 集装箱岸桥结构模型

有限元模型如图2所示，该模型采用三维beam 188单元建模。计算中在各立柱基底处沿小车运行方向输入EL-Centro波，步长取0.02 s。

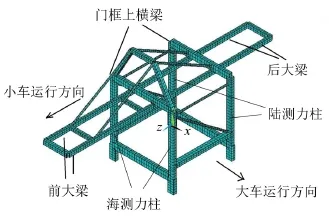
图2 集装箱起重机有限元模型

2.2 不同阻尼模型下岸桥缩比模型地震反应

为了比较不同阻尼系数下的岸桥结构的地震响应，采用工程上最常用的4种不同的Rayleigh阻尼系数，对同一岸桥结构模型进行动力时程分析。

采用上文中方法确定的四组阻尼模型分别计为R1、R2、R3、R4，经时程数值计算，测点S 6的加速度时程曲线如图3所示，测点位置布置如图5所示。

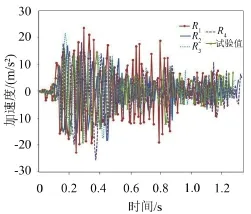
图3 考察点S 6的加速度时程曲线

2.3 岸桥缩比模型振动试验

采用振动台相似模型地震模拟试验来验证数值计算的结果，通过对比分析，找出与试验结果最接近的数值计算结果。试验现场如图4所示，岸桥结构相似缩比模型的相似系数见表1。试验地点为武汉理工大学交通部重点实验室，振动台主要参数为：台面尺寸1 500 mm×1 500 mm，水平方向最大加速度± 50 m/s2，竖直方向最大加速度±30 m/s2，水平方向最大位移±200 mm，竖直方向最大位移±100 mm，水平方向最大速度均为0.8 m/s，竖直方向最大速度为0.8 m/s，最大承载力2 t，频率范围0.1 Hz～100 Hz。对于岸桥缩尺模型而言，地震载荷的时间轴被调整为原型的1/15，加速度峰值则被调整为原型的15倍[9]。处理后地震波的时间很短，试验过程相对较快，在数据采集时，可将数据采集系统的采样频率调整得高一些[10]。

图4 试验现场图

表1 岸桥相似模型相似关系

在模型上取一组测量点（这些测量点的选取都是基于现实情况下岸桥结构的危险发生点或者是便于测量的点），如图5所示，从模型支座基底依次向上选取5个测量点：S 1、S 3、S 6、S 8、S 12，考察其加速度放大系数。

图5 模型测量点

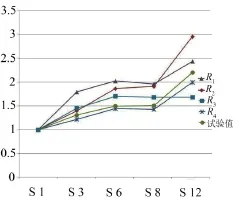
图6 加速度放大系数曲线

观察图3、图6可以看出，与试验值最为接近的是R 4，即采用上文1.1中方法（4）所确定的阻尼模型与试验结果最相似。方法（4）既考虑了结构的频率特性，也考虑了地震动的频谱特性，使得R4阻尼模型计算结果与试验值最为接近。采用方法（1）低估了频率范围内的阻尼，导致结构动力反应偏高，使得加速度放大系数明显高于其他方法采用的阻尼模型；对于基础下方有深厚覆盖层的场地来说，使用其基频来确定是不合理的。采用方法（2）低估了ωa，ωb之间的阻尼，高估了频率范围之外的阻尼，一般情况下计算的动力反应偏高。方法（3）可以部分弥补所低估的ωa，ωb之间的阻尼比，使得结果比较接近试验值。

3 岸桥原型地震反应

对岸桥全尺寸原型进行地震时程分析，使用R 4阻尼模型，将其数值计算结果进行相似系数变换，并与缩比模型试验值比较。

给出考察点S 11的加速度时程曲线和考察点S 5的应变时程曲线，如图7—图8所示。图中曲线包括原型计算值和缩尺模型试验值，图中原型时程计算值已经过相似比系数转换。

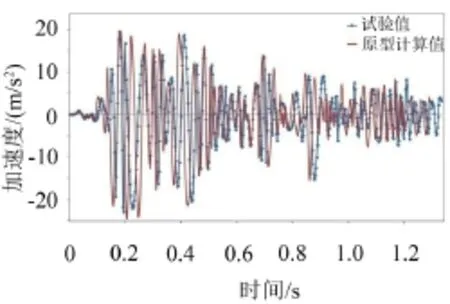
图7 考察点S 11的加速度时程曲线

图8 考察点S 5的应变时程曲线

观察图7—图8、表2，对比数值计算和试验结果可知，试验结果与数值计算的结果有一定误差，在地震载荷下考察点加速度、应变出现极值大小以及对应时间都比较近似。误差在一定许可范围内、试验结果总体与数值计算结果相近，说明时程分析所选取的阻尼模型R 4是正确的，同时也使得相似缩比模型的有效性得到了进一步的验证。

表2 不同测点的最大动态应变

4 结语

有限元时程分析中，不同阻尼模型对结构地震反应的影响是不可忽略的。采用不同的阻尼模型，对同一岸桥结构缩比模型进行动力时程分析，比较不同阻尼模型下的结构地震响应，并与振动台地震模拟试验所得的试验值进行了比较，选出与试验结果最相近的阻尼模型。将该阻尼模型用在岸桥原型的动力时程分析中，并与缩比模型试验结果进行比较，结果表明：

（1）对岸桥结构进行时程数值计算时阻尼模型在很大程度上影响计算的精度，其影响不能忽略。

（2）采用阻尼模型R 4与试验所得结果最为接近，且岸桥结构原型的数值计算结果也证明了选用R4的正确性。

（3）振动台地震模拟试验中使用的岸桥结构缩尺模型是可行的，能为后续的研究提供一个可靠的试验对象。

（4）R 4在本文模型结构数值时程分析中取得理想结果，但是其他结构是否适用还不清楚，需要用试验手段或其他方法进行验证；地震波的选取对试验结果也有较大影响，不同地震波具有不同的卓越频率，使得R 4在不同地震条件下计算所得结果有较大出入，需进行多条地震波下结构的数值计算及试验模拟。

[1]李哲，王贡献，王东，等.大型集装箱起重机地震动力学行为试验方法研究[J].武汉理工大学学报，2013，35(8)：72-76.

[2]楼梦麟，张静.大跨度拱桥地震反应分析中阻尼模型的讨论[J].振动与冲击，2009，28(5)：23-28.

[3]Jin Y L,Li Z G.Theoretical design and experimental verification of a 1/50 scale model of a quayside container crane [J].Proceedings of the Institution of Mechanical Engineers,Part C:Journal of Mechanical Engineering Science,2012,226(6):1644-1662.

[4]L D Jacobs,Reginald DesRoches,Roberto T Leon.Seismic behavior of a jumbo container crane including uplift [J].Earthquake spectra,2011,27(3),745-773.

[5]L D Jacobs,Reginald DesRoches,Roberto T Leon.Experimental study of the seismic response of container cranes [J].Ports 2010:Building on the Past,Respecting the Future 210 Don’t Mess with Structural Engineers 2010 ASCE,91-99.

[6]邹德高，徐斌，孔宪京.瑞利阻尼系数确定方法对高土石坝地震反应的影响研究[J].岩土力学，2011，32(3)：797-803.

[7]Yoshida N,Kobayashi S,Suetomi I,et al.Equivalent linear method considering frequency dependent characteristics of stiffness and damping[J].Soil Dynamics and Earthquake Engineering,2002,22(3):205-222.

[8]Hudson M,Idriss I M,Beikae M.User manual for QUAD 4 m:A computer program to evaluate the seismic response of soil structures using finite element procedures and incorporating a compliant base[D]:Berkeley:University of California,1994.

[9]吕平，高金岗，李晶，等.影响约束阻尼结构阻尼性能的因素[J].噪声与振动控制，2014，34(5)：234-238.

[10]金玉龙，吴天行.集装箱码头岸桥结构的动力相似分析与试验验证[J].上海交通大学学报(自然科学版)，2012，46(10)：1609-1615.

Discussion on Damping Models for Seismic ResponseAnalysis of Container Cranes

LIZhe,WANG Gong-xian,HU Ji-quan,WANG Dong
（School of Logistics Engineering,Wuhan University of Technology,Wuhan 430063,China)

It is difficult to make seismic tests for large-scale structures,so,the proportionally reduced model and finite element method can be applied to time-history test and analysis of the structures.In the numerical analysis of the structure of a container crane,it was found that the damping model had a significant effect on the computation accuracy for the time-history analysis.Then,four different conventional Rayleigh damping models were employed for time-history dynamic analysis for the 1:15 scaled model of the container crane.The results were compared with the measurement data obtained in the earthquake simulation testing.The damping model which results were closest to the measurement data in the testing was chosen and applied to the time-history dynamic analysis of the container crane prototype.After the similarity factor transformation, the results were compared with those of the scaled model test.It was found that the tolerance between the two results was within the allowable range,which means that this damping model is correct and the reliability of the scaled model is verified.

vibration and wave;damping model;time-history analysis;container crane structure;shaking table test;scale model

TH247

A

10.3969/j.issn.1006-1335.2015.02.004

1006-1355(2015)02-0015-04

2014－10－17

国家自然基金资助项目（51275369）

李哲（1986－），男，武汉理工大学物流工程学院博士研究生，主要研究方向：先进设计理论与方法。

王贡献（1976－），男，副教授，武汉理工大学；主要研究方向：结构动力学与试验研究。E-mail:wanggongxian@gmail.com