海流冲击对深海采矿装备液压管道流固耦合振动的影响

周知进，陈 雄，康红军，何 星

(湖南科技大学 机电工程学院，湖南 湘潭 411201)

海流冲击对深海采矿装备液压管道流固耦合振动的影响

周知进，陈 雄，康红军，何 星

(湖南科技大学 机电工程学院，湖南 湘潭 411201)

为研究海流冲击对深海采矿装备液压管道流固耦合振动的影响，利用伯努利—梁模型，对内流作用下的柔性管道进行受力分析，建立管道流体流固耦合振动方程。根据有无外部周期性冲击作用力两种情况对液压系统管道进行了仿真。仿真结果表明：(1)外部周期性冲击力加剧了管道内部的油压波动。(2)外部周期性冲击力增大液压管道振动的最大位移。

振动与波；液压管道振动；油压波动；流固耦合；外部冲击作用力

管道系统作为一种具有代表性的流体输送系统，在电力，航空航天，石油化工等领域有着重要的意义。而管道系统输送安全，一直是各界所关注的焦点。管道的安全事故主要是因为管道和管道内流体的耦合振动，引发系统失稳。脉动的流体对流固耦合作用的引发最为突出，因此，脉动流体引发的流固耦合振动问题，自然成为国内外学者研究的热点。Paidoussis等人[1]证明一定频率和振幅的内流脉动使原来不稳定管道可能变得稳定。Holmes等人[2]得到了一些稳定流的重要非线性研究成果。Panda等人[3]对脉动流体非线性动力学也进行了研究。李宝辉等人[4]基于有限元理论，考虑了管道的流固耦合振动，提出了有限元-传递矩阵法的概念，并给出了外力作用下的管道流固耦合振动的有限元-传递矩阵。刘桂斋等人[5]通过两端弹性支承的固管受内外流共同作用的模型,推导了管道与流体间的耦合振动方程，并用Galerkin模态受加法对管道的动态特性进行了分析。佟琨等人[6]通过ansys cfx对液压回油管路进行了流固耦合分析，找到了几种解决流固耦合振动问题的方法。税朗泉等人[7]对含有脉动流体轴向周期激励的两端简支输流管道横向振动稳定性的影响进行了研究。李兵等人[8]讨论了流体对两端固支薄壁圆柱管振动频率的影响，并做了详细的实验研究，对工业应用有着重要的现实意义。目前针对深海环境下采矿机械液压系统管道内部油压波动引发的管道振动研究较少，为了解决深海采矿机械液压系统管道振动引起的稳定性和液压元件疲劳损伤问题，有必要对深海环境液压系统管道流固耦合振动展开深入研究。

1 内流作用的下的流固耦合振动方程

管道结构模型选用伯努利—粱模型，忽略管道的阻尼，得出下面的管道结构振动方程。

图1 管道的横向截面

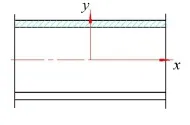
图2 管道的纵向截面

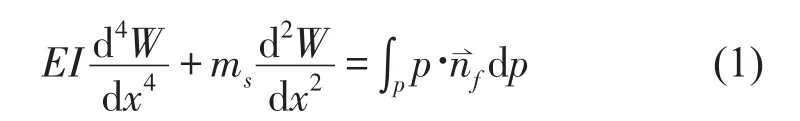
图3 管道没有发生弯曲之前的速度矢量

图4 管道弯曲变形后的速度矢量

根据流量守恒定律可知

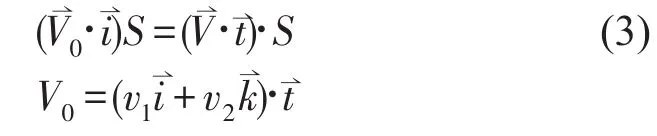
由耦合条件可知

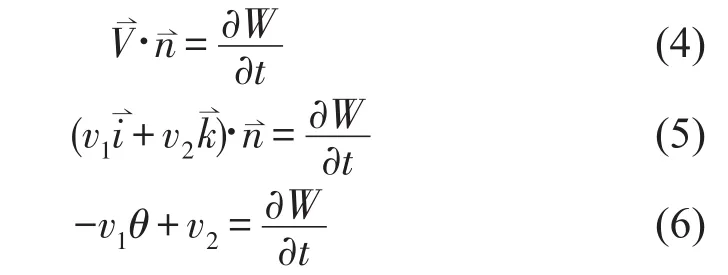
根据流体动量守恒定律可得

在微段δx上

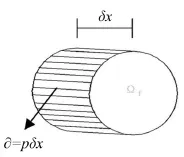
图5 微元的横截面

图6 微元的纵向截面

（9），（10）两个积分在k⇀方向的投影：

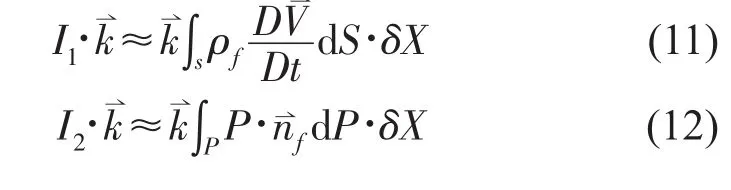
由于

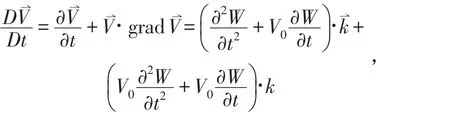
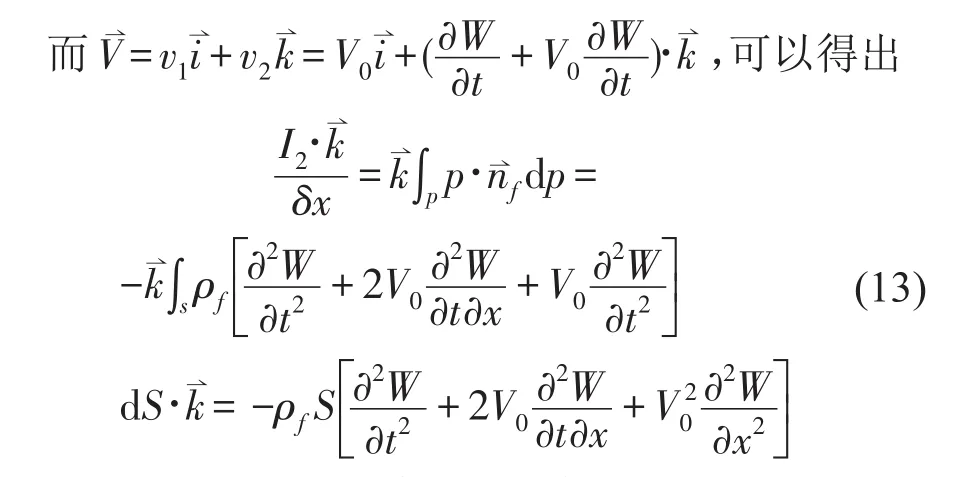
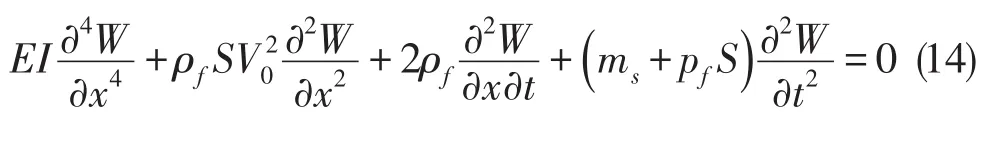
2 管道系统振动有限元描述

用U和W表示管道单元的纵向位移和横向位移，则有：U=Aσe；W=Bσe。式中：A，B为管道的形状函数，σe为管道节点单元。采用二节点元，其表达是如下

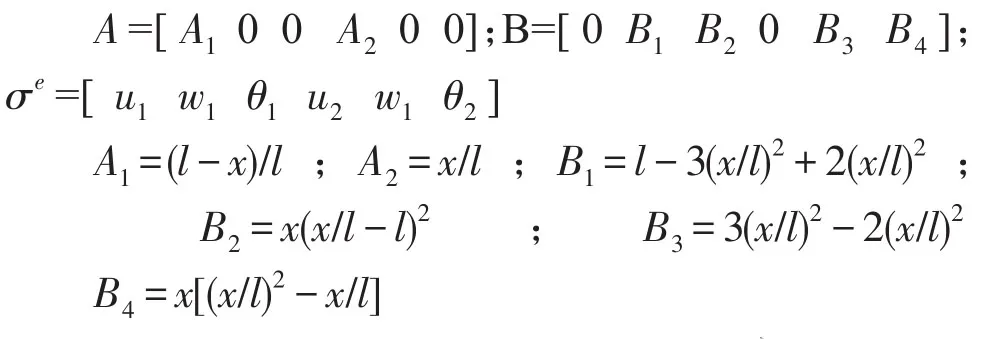
式中l为长度，x为单元轴向方向的横坐标。

管道系统结构运动的微分方程

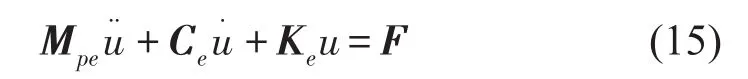
Mpe，Ce，Ke分别为管道的结构，阻尼，刚度矩阵。u为管道的振动速度，F为外载荷。

Mle和Mae分别表示管道的横向和轴向振动质量矩阵，Kbe和Kae分别表示管道弯曲和轴向刚度矩阵。

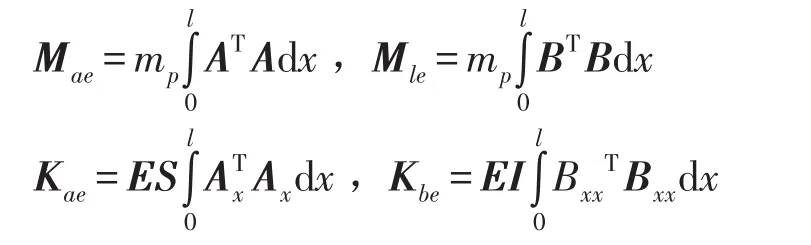
mp为单位长度管带质量，S为管道截面面积，E为弹性模量，I为管道截面对x轴的惯性矩下标x表示对x求偏导。

忽略管道阻尼的影响，可以得出管道的结构振动方程为

3 流体的波动方程

有黏可压缩流体在小扰动条件下，可将流体连续性方程简化得到声学波动方程

式中C为流体介质的声速。

对上式乘以一个虚压力，利用Galerkin法在整个流域内进行积分。然后对压力和位移进行离散化，可以达到离散的波动方程

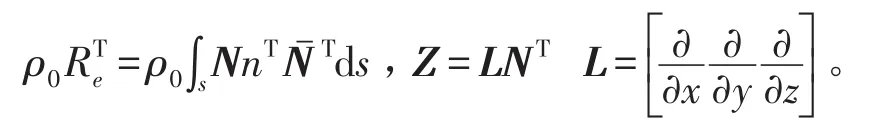
Mfe，Kef分为流体的质量矩阵和刚度矩阵，为流固耦合截面的耦合质量矩阵，pe为压力节点，ue为单元节点位移矢量，L为矩阵算子，v表示整个流域，s表示流固耦合接触面，n为接触面的法向量。

在流固耦合接触面，存在流体—结构的相互耦合作用，流体的压力对结构会产生一个面力，把流体作用在结构单元的面力代入到结构的振动方程(16)中得出

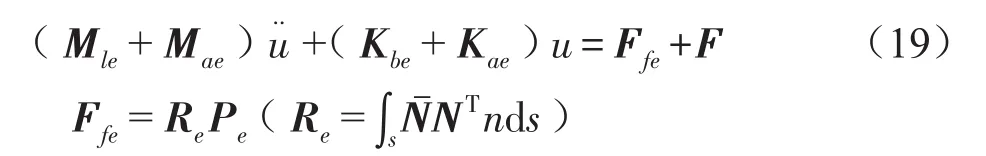
将Ffe=RePe代入结构振动方程中可得

结合流体的波动方程和结构的振动方程，可以得出流体-结构耦合的有限元离散方程

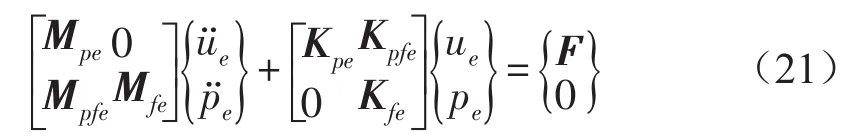
式中Mpfe=ρ0ReTKpfe=-Re

4 流固耦合振动有限元分析

4.1 物理模型建模

考虑管道内壁半径为25.4 mm，外径为38.1 mm，管道长度为1 000 mm。导入workbench的Geometry中，在材料模块中建立液压管道材料，设置管道材料的密度为3.15×103kg·m-3，弹性模量为4×1010Pa，泊松比0.4。内部流体采用HPL 46液压油，液压油的密度880kg·m-3，动力粘度0.040 48 Pa·s。管道进口端的油液施加脉动的压力，出口端液压设置为1 MPa。

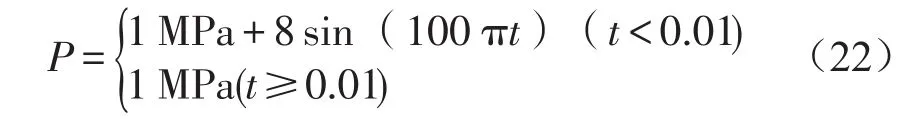
4.2 仿真结果及分析

运用workbench中的cfx以及瞬态结构分析模块进行流固耦合仿真，先对不加载外部周期冲击力和加载外部周期冲击力F=5×104sin(100 πt)两种情况进行流固耦合仿真计算，然后对外部周期冲击作用力下的液压管道进行瞬态的结构仿真，通过三者仿真结果的对比，来分析外部周期冲击作用力对管道流固耦合振动的影响。设置流固耦合仿真时间为0.1 s，时间步长为0.001 s，管道的支撑方式为两端固支，因为波浪冲击是对整个管道而言的，所以周期力作用的区域为管道的外表面，力的方向为垂直于管道表面向里。

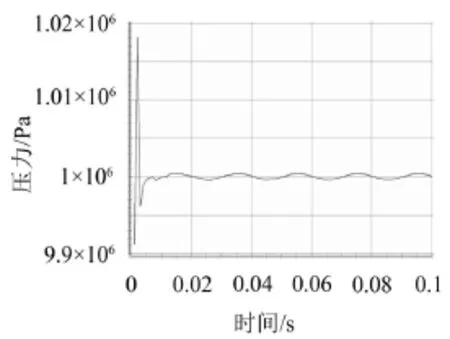
图7 外部周期冲击作用力下的油压波动

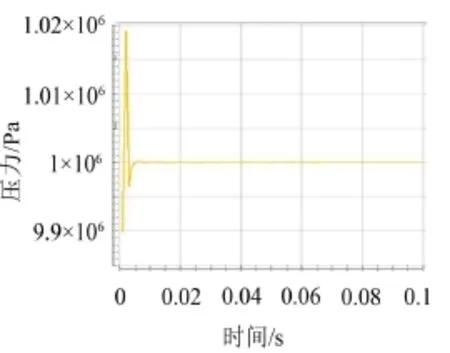
图8 内部流固耦合作用下的油压波动

图7和图8分别为有无外部周期冲击作用力管道系统流固耦合作用下流体域监测点压力随时间波动曲线，从曲线中可以看出，在内部压力波动较大，即t＜0.01 s时，图1和图2相差不大，说明此时外部周期力对油压的影响相对于内部油压波动而言较小，而当t＞0.01 s时，我们可以从图7中看出，监测点的压力在0.02 s后出现周期性波动，波动振幅为2 000，而在图8中，我们发现监测点内部压力波动很小，并且在t＞0.08 s后，油压停止波动。通过二者仿真结果的对比我们可以得到这样的结论，外部周期冲击作用力加剧了液压管道内部油压的波动。

图9 管道内部流固耦合振动0.1 s时的位移云图

图9中我们可以看出，管道系统只受到波动油压，产生流固耦合振动时，管道振动的最大位移为5.412 717×10-6m。从图10中我们可以看出，管道结构在受到5×104sin（100 πt）的外部冲击作用力时，管道振动的最大位移为1.504 6×10-5m。从图11中我们可以看出，管道在受到外部周期冲击作用力和波动的油压共同作用时，管道振动的最大位移为2.23×10-5m。通对比较我们可以看出，液压管道在受到外部周期冲击作用力和波动油压共同作用时的振动位移大于前二者之和，由此可以说明，外部周期冲击作用力加剧了管道系统的流固耦合作用，从而增大了管道振动的最大位移。

图 10外部周期冲击作用力下管道0.1 s时的位移云图

图11 外部周期力下管道耦合振动0.1 s时的位移云图

5 结语

通过三种仿真结果的对比，我们可以得出以下结论：

（1）外部周期冲击作用力加剧了液压管道内部的油压波动；

（2）外部周期冲击作用力增大了液压管道振动的最大位移，即外部激励加剧了管道系统的振动。

流体激励部分，所以结果与真实情况存在较大误差。而泵出口处流动状态已慢慢趋于平稳，所以计算结果与实验值相对较为接近。

Influence of Ocean Current Impact on Fluid-structure Coupled Vibration of Deep-sea Mining Equipment’s Hydraulic Pipelines

ZHOU Zhi-jin,CHEN Xiong,KANG Hong-jun,HE Xing
(Mechanical and Electrical Engineering College,Hunan University of Science and Technology, Xiangtan 411201,Hunan China)

The Bernoulli-beam model was employed to study the influence of ocean current impact on fluid-structure coupled vibration of the deep-sea mining equipment hydraulic pipeline.Through the dynamic analysis of the flexible pipeline under internal fluid flow,the fluid-structure coupled vibration equations were established.The behavior of the hydraulic pipeline with and without external periodic impact was simulated respectively.The simulation results show that the external periodic impact can exacerbate the fluid pressure fluctuation in the pipeline and increase the maximum displacement of the hydraulic pipeline vibration.

vibration and wave;hydraulic pipeline vibration;hydraulic oil pressure fluctuation;fluid-structure coupling;externalperiodic impact

IO353.1

A

10.3969/j.issn.1006-1335.2015.02.002

1006-1355(2015)02-0007-04+111

2014－10－15

国家自然科学基金（21479073）；湖南省教育厅科技计划项目（13A024）

周知进（1969－），博士，教授，硕士研究生导师。主要从事深海矿产资源开发装备的研究。E-mail:zjzhou@hnust.edu.cn.