基于柱面近场声全息的水下航行器辐射声场重构

万海波，朱石坚，楼京俊，张若愚

（1.海军工程大学 动力工程学院，武汉 430033 2.哈尔滨工程大学 水声工程学院，哈尔滨 150001）

基于柱面近场声全息的水下航行器辐射声场重构

万海波1，朱石坚1，楼京俊1，张若愚2

（1.海军工程大学 动力工程学院，武汉 430033 2.哈尔滨工程大学 水声工程学院，哈尔滨 150001）

为了解决水下航行器这种柱形噪声源的定位与识别问题，采用柱面近场声全息技术，研究了辐射声场重构。利用声场仿真分析验证采用该方法进行声场重构的正确性，并对测试过程中基阵测试距离、全息面阵元位置误差以及相位误差对声场重构精度的影响进行分析。最后开展了水下航行器舱段模型的柱面近场声全息试验研究，得到了舱段内部电磁激振器的水下辐射声场和位置信息，验证了该方法的可行性和有效性。

声学；水下航行器；柱面近场声全息；声场重构；影响因素；试验

鱼雷、潜艇等水下航行器的水下辐射噪声是评估其声隐身性能的重要指标，明确其噪声源的位置、声辐射特性，对制定合理的控制方案、提高其声隐身性能具有重要的研究意义和工程价值。随着水声学和信号处理技术的发展，近场声全息技术取得了长足的进步，不仅利用了声波的幅度信息，还利用了声波的相位信息，可以根据采集的声压数据通过信号处理和反演计算，获得三维空间中任何感兴趣的位置的声场信息和噪声源指向性信息[1]。因此，广泛应用于噪声源的定位与识别领域。

理论上，近场声全息算法包括声场空间变换法[2]、边界元法[3]以及等效源法[4]，其中声场空间变换法由于简单实用、分辨率较高、计算准确高效，因此工程实用性最强。然而该方法要求声源表面形状规则，且测量面与声源面共形。国内学者对该方法进行了大量的理论和实验研究[5-7]，不过往往偏重于平面近场声全息问题，对于水下航行器这种柱形声源，若仍然采用平面近场声全息技术来进行噪声源定位与识别，必然会引起较大的误差。

针对该问题，本文采用柱面近场声全息技术，对水下航行器的噪声源进行定位。首先通过仿真分析验证了采用该方法进行声场重构的正确性，随后对测试过程中基阵测试距离、全息面阵元位置误差以及相位误差对声场重构精度的影响进行了分析，最后开展了水下航行器舱段模型的柱面近场声全息试验研究，得到了舱段内部电磁激振器的水下辐射声场和位置信息，进一步验证了该方法的可行性和有效性，旨在为柱面近场声全息技术的工程应用提供一定参考。

1 柱面近场声全息的基本原理

由均匀理想流体媒质中小振幅声波的波动方程，可以得到Helmholtz方程

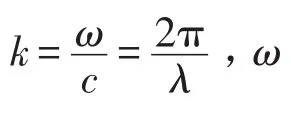
将直角坐标系转换为柱面坐标系，令x=rcosθ，y=rsinθ，则Laplace算子可以表示为

采用分离变量法，假定式（1）的解为

则柱面坐标系下的Helmholtz方程可以表示为

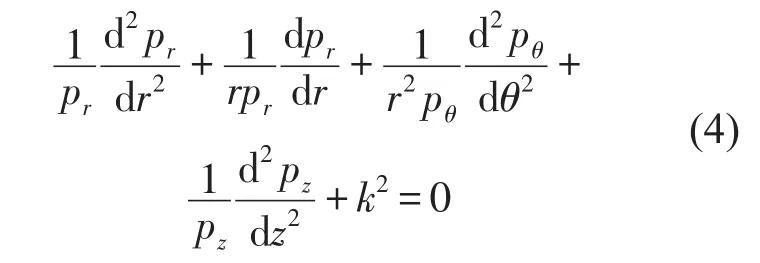
由式（4）可以看出，pz项仅与坐标z有关，因此必然等于常数，可令

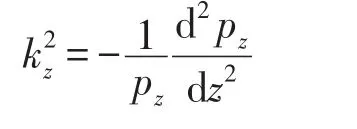
同时，定义

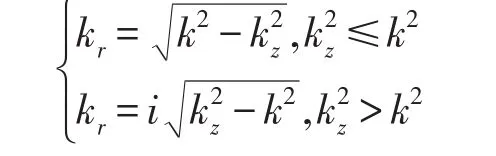
可以得到式（1）的通解[8]

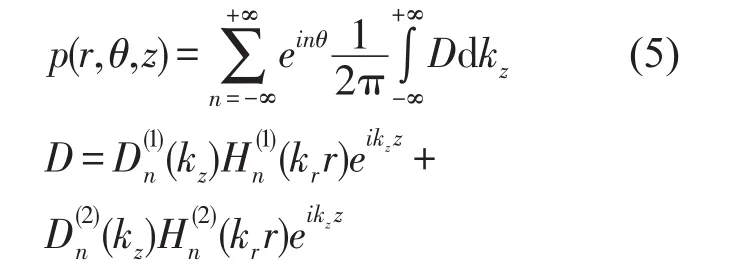
其中D1(kz)、D2(kz)均为任意常数；分别代表阶数为n的第一类和第二类Hankel函数，对应向外发散的波和向内收敛的波。

对于水下航行器，关注重点往往是由源面向外的辐射声场问题，因此仅需求出即可。若将Fourier级数也看作广义的Fourier变换，那么便可以看作是p(r,θ,z)的二维Fourier变换

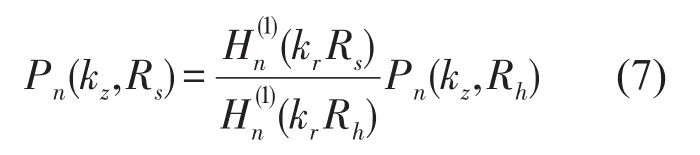
式中Pn(kz,Rs)，Pn(kz,Rh)分别为重建面r=Rs和全息面r=Rh上声压二维Fourier变换。

根据Euler公式，可以得到重建面上径向振速与声压之间的关系，进一步可得到重建面上的径向振速分布同全息面上的声压分布之间的关系

式中Vn(kz,Rs)是径向振速v(Rs,θ,z)分布的二维Fourier变换。

因此，对全息测量面上测得的声压p(Rh,θ,z)做二维Fourier变换，便可以得到重建面上的声压和径向振速的二维Fourier变换，最后通过逆Fourier变换即可得到重建面上的声压和振速，进而可以求出柱面上的声强分布。

为了分析柱面近场声全息声场重构的精度以及测量参数对重构结果的影响，采用相对方式计算全息变换产生的误差，具体定义如下

2 仿真分析

2.1 柱面近场声全息算法仿真

下面通过数值仿真分析验证柱面近场声全息算法的有效性。仿真采用两个脉动球声源，双声源半径各为0.05 m，全息测点空间分布为轴向间距300 mm，周向间距为2.86°，为模拟水下航行器辐射噪声，以双声源所在线为圆柱轴线，坐标原点位于双声源中心，以轴向半径5.5 m为水下航行器壳体，脉动球声源间距r为1 m，振动频率为20 Hz，全息测量距离D为0.5 m，重构距离d为0.3 m，其中测量距离为壳体向外辐射距离，重构距离为逆向重建时与全息面的距离，仿真采用快照法[9]。

图1为全息面理论声压幅值，图2和图3分别为重建面全息重构和理论声压幅值。通过对比可以看出，在全息测量面上已经不能区分两个相干声源，而通过柱面近场全息重建，可以准确地对声源进行识别与定位，且声源位置、声压幅值与理论值基本一致，这充分地验证了水下航行器辐射声场全息重构的正确性，同时也表明近场声全息技术具有不受瑞利判据限制的较高重建分辨率。

图1 全息面理论声压幅值

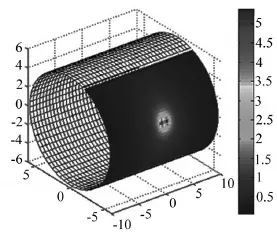
图2 重建面全息重构声压幅值

图3 重建面理论声压幅值

2.2 测量参数对声场重构误差的影响分析

测试参数直接决定了水下航行器辐射声场全息重构的精度，下面就不同全息测量距离D、不同阵元位置误差Le以及不同阵元相位误差Ae对声场重构误差的影响进行仿真分析，其中脉动球声源间距r为4 m，振动频率分别为20 Hz、25 Hz、31.5 Hz、40 Hz、50 Hz、63 Hz、80 Hz、100 Hz、125 Hz、160 Hz、200 Hz、250 Hz、315 Hz、400 Hz、500 Hz、630 Hz、800 Hz、1 000 Hz，重构距离d为0.3 m。

测试实施过程中，首先需要确定基阵的测量距离。图4为测量距离分别为0.3 m、0.5 m、0.8 m、1.0 m的情况下，重构声场与理论声场幅值的误差曲线，可以看出，柱面近场声全息算法能够很好地对声源进行识别与定位，同时由于全息测量能够获得沿法线方向衰减很快的倏逝波成分，因而，测量距离尽量靠近声源面才能获得较高的重建精度。

图4 不同测量距离对声场重构的影响

当测量基阵受到水流影响，阵元容易产生位置误差。图5为基阵测量距离为0.5 m情况下，阵元位置随机误差最大值分别为0.01 m、0.10 m、0.20 m时，重构声场与理论声场幅值的误差曲线。可以看出，阵元的位置误差对柱面近场声全息重建精度有较大的影响，位置误差越大、重建频率越高，重建精度就越低。实际应用过程中，需要在低流速情况下开展测试。

图5 不同阵元位置误差对声场重构的影响

声场重构过程中，需要测得全息面声场的相位信息，当不能准确获得不受干扰的参考信号时，全息测量面相位的误差对全息重建精度的影响便不容忽视。图6为基阵测量距离为0.5 m情况下，阵元相位随机误差最大值分别为1°、5°、10°时，重构声场与理论声场幅值的误差曲线。可以看出，阵元的相位误差造成的全息重建误差较位置误差造成的全息重建误差要大得多，因此，在柱面近场声全息测试过程中，只有获得纯净的、不受干扰的参考信号，才能准确得到全息测量面相位信息，进而实现声场重构。

图6 不同阵元相位误差对声场重构的影响

3 试验分析

为了进一步验证柱面近场声全息技术的有效性和可行性，开展了柱面近场声全息试验研究。选用单层壳体舱段模型作为试验对象，模型径向长1 450 mm，半径为510 mm，其内部安装有电磁式激振器作为振源（激振器安装在壳体下方，距离端部600 mm），利用多边形固定架放置水听器，从而构成共形测试阵列，该阵列可通过操控电机沿轴向和径向运动，具体如图7所示。

图7 舱段测试模型

试验过程中，采用NoisExpert软件[10]完成运动控制和数据采集，其中电磁激振器的激励频率为920 Hz，全息面测量距离壳体为710 mm，轴向采样间隔为50 mm，径向采样间隔为5°，重构距离为550 mm。

图8 全息面声压分布

图9 重构面声压分布

图8和图9分别为全息测量面和重构面声压分布图，其中横坐标为舱段模型周向角度，纵坐标为舱段模型轴向距离。可以看出，通过柱面近场声全息技术可以准确地对舱段模型噪声源的辐射声场进行重构，并且可以清楚地看到噪声源的位置信息（图中椭圆位置），与模型中激振器的安装位置基本一致。因此，柱面近场声全息技术完全可以准确、有效地实现水下航行器这种柱形噪声源的定位与识别。

4 结语

针对水下航行器这种柱形噪声源的定位与识别问题，本文采用柱面近场声全息技术进行了研究，通过声场仿真分析得出如下结论：

（1）柱面近场全息技术可以准确地对水下航行器声源进行识别与定位，且具有不受瑞利判据限制的较高重建分辨率；

（2）测试过程中，基阵测量距离尽量靠近声源面才能获得较高的重建精度；全息测量面阵元的位置误差和相位误差对柱面近场声全息重建精度有较大的影响，并且相位误差较位置误差造成的声场重建误差要大得多，测试过程中必须确保阵元位置和相位的准确性；

（3）柱面近场声全息技术可以准确地对舱段模型噪声源的辐射声场进行重构，并且可以清楚地看到噪声源的位置信息(与模型中激振器的安装位置基本一致)。

[1]Yang-Hann Kim.Can we hear the shape of a noise source? [R].The 18thInternational Congress on Acoustic(ICA 2004),Kyoto International Conference Hall,Japan,April 4 to 9,2004.

[2]Maynard J D,Williams E G Lee Y.Near field acoustical holography I:Theory of generalized holography and the development of NAH[J].J.Acoust.Soc.Am.,1985,78(4): 1395-1413.

[3]张海滨，蒋伟康，万泉.边界元法循环平稳近场声全息理论研究[J].声学学报，2008，33(3)：231-237.

[4]孙超，何元安，刘月婵，等.圆柱壳辐射声场重构的波叠加方法[J].噪声与振动控制，2012，10(5)：31-36．

[5]罗禹贡，李克强，郑四发，等.平面近场声全息重建结果不准确性问题的研究[J].声学学报，2003，28(6)：555-560.

[6]李凌志，李俊，卢炳武，等.平面近场声全息中正则化参数的确定[J].声学学报，2010，35(2)：169-178．

[7]李青，毕传兴，徐亮.基于Labview的近场声全息噪声源识别系统[J].噪声与振动控制，2010，12(6)：140-144．

[8]于飞，陈剑，周广林，等.声源识别的柱面声全息方法与数值实现研究[J].振动工程学报，2004，17(3)：354-358．

[9]L S Jarry.A turiac on underater acoustic imaging[J]. Acoustic Imaging,1979,9:599-630．

[10]张若愚.半空间柱面声全息及可视化[D].哈尔滨：哈尔滨工程大学，2009，2.

Reconstruction ofAUV RadiationAcoustic Fields Based on Cylindrical NAH

WAN Hai-bo1,ZHU Shi-jian1,LOU Jing-jun1,ZHANG Ruo-yu2
（1.College of Power Engineering,Naval University of Engineering,Wuhan 430033,China; 2.UnderwaterAcoustic Engineering,Harbin Engineering University,Harbin 150001,China）

The cylindrical near-field acoustic holography(NAH)method was proposed for localizing and identifying the noise sources of the AUV.Reconstruction of the radiation sound fields was studied.The feasibility and correctness of this method for sound field reconstruction were verified by the acoustic field simulation.The influences of the array test distance, position errors of the holographic planar array and the reconstruction phase errors on the accuracy of the sound field reconstruction were analyzed.Furthermore,the radiation acoustic field and the location information of the electromagnetic actuator in the cabin model were obtained by the method of cylindrical NAH.The experimental result shows that the radiation acoustic field of theAUV can be reconstructed correctly and effectively with this method.

acoustics;AUV;cylindrical NAH;sound field reconstruction;influencing factors;experiment

O322

A

10.3969/j.issn.1006-1335.2015.02.005

1006-1355(2015)02-0019-05

2014－09－14

万海波(1987－)，男，河南省南阳市人，博士，目前从事振动与噪声控制方面研究。E-mail:general3000@126.com