利用几何常数对赋范空间特征性质的研究*
2015-12-02张宏蕃王琍梅王晓丹
张宏蕃,王琍梅,王晓丹
(黑龙江工程学院)
0 引言
几何问题可以定性或定量加以描述,几何常数是其定量描述,通过研究空间几何常数及其取值范围,可以得到其相关几何性质的有无,研究非方常数是一种重要的方法.20世纪80年代开始,包括波兰与中国相关学者在有关空间几何理论等方向得到了很好的结论,为该学科的发展做出了大量的贡献,例如凸性,凹性及非方性等都找到了充要判别准则;在此基础上也开始了从定性到定量的升华.20世纪90年代,Gao J和 Lau K S在James意义下和Schaffer意义下给出了非方常数[1],给出空间中非方常数等价于一致非方的;若dim(X)≥2则1≤CS(X)≤CJ(X)≤2和CJ(X)CS(X)=2成立;空间非方常数CJ(X)<3/2蕴含着空间X具有一致正规结构.2011年文章[5]引入新的几何常数,并给出下界,证明了一个Banach空间X是一致非方当且仅当h(X)>1/2,2012年文章[6]给出利用度量椭圆给出内积空间的一个特征性质.若空间具有不动点则其为一致正规结构,故在理论上对非方常数的研究十分重要.点态几何常数的计算、估计及表示是其主要的研究问题,能够量化的给出点态的几何性质与相关几何常数的空间局部性质.可以通过对赋Orlicz范数或赋Luxemburg范数Orlicz序列空间中满足相关条件的非方常数之间的关系进行研究,得到Orlicz空间中非方常数的有关结论,进而会使得该方向的研究结果更加系统,并在精确计算方面提供了有重要价值的理论公式.
1 预备知识
定义1 Minkowski平面是实二维赋范线性空间,设X是一个Minkowski平面,‖·‖是 X上的范数,集合:
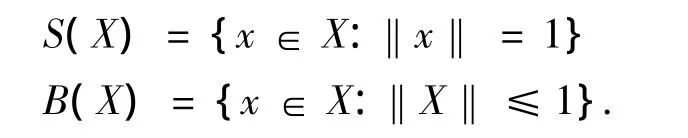
分别称为X的单位球面和单位球.
James在1964年提出一致非方空间时给出了非方常数的概念[1]如下.定义2 一个赋范线性空间X,常数:
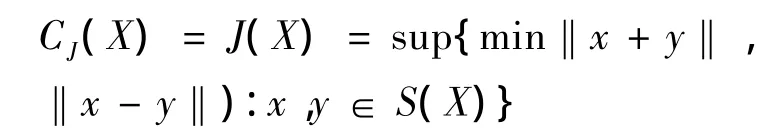
称为X的非方常数或者James非方常数,
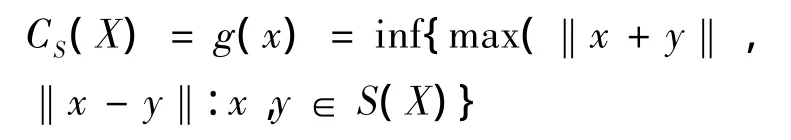
称为X的非方常数或者Schaffer非方常数,
1994年计东海,王廷辅[1]给出了两种定义下非方常数的等价定义表达式:

2 主要内容
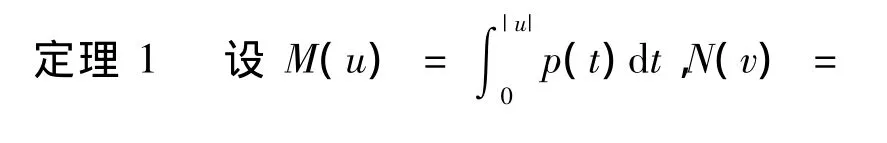



3 结束语
该文通过对赋Orlicz范数或赋Luxemburg范数Orlicz序列空间中满足相关条件的非方常数之间的关系进行研究,得到生成函数的导数满足凹或凸性质时非方常数的关系并且对其进行了证明,进而由于该文关于Orlicz空间非方常数的工作使得该方向的研究结果更加系统,并在精确计算方面提供了有重要价值的理论公式.
[1] James R C.Uniformly Nonsquare Banach Spaces[J].Ann of Math,1964,80:542-550.
[2] Gao J,Jau K S.On the Geometry of Spaces in Normed Spaces[J].J Austral,Math Soc A,1990,48:101-112.
[3] Ji Donghai,Wang Tingfu.Nonsquare Constants of Normed Spaces[J].Acta Sci Math Szeged,1994,59:421-428.
[4] Ji D H,Wang D P.Some Equivalent Representations of Nonsquare Constants and Its Applications[J].Northeast Math J,1999,15:439-444.
[5] 倪柏竹,何婵,计东海.一致非方空间的新特征性质[J].哈尔滨理工大学学报,2011(1):105-108.
[6] 计东海,陶冶.度量椭圆与欧氏空间的一个特征性质[J].哈尔滨理工大学学报,2012(5):84-86.
