QM/MM方法的研究*

刘景林，曹亚杰，吴云飞

(佳木斯大学)

0 引言

分子动力学方法是较成熟的模拟方法之一，其可以对由千万个原子构成的生物大分子体系进行高效地模拟计算．但由于其是以经典力学为基础的，无法充分地描述电子的运动，在二十世纪初诞生的量子力学能够充分的地描述电子运动，现今应用量子力学方法已经可以对电子运动进行精确的计算，但是由于其需要进行大量的并且及其复杂的积分运算，其结果就是产生了巨大的运算量，并且严重的增加了计算成本．即使在现今最优秀的计算环境下，也无法很好地进行这种大规模的运算，这种大规模的运算在化学、生物学等多门学科的发展中占有重要的地位，为了可以高效地进行这种大规模的运算，既能得到精确的结果，同时可以有效地降低计算成本，则应运而生了被称作QM/MM方法的混合动力学计算方法，这是采用量子力学(Quantum Mechanics，QM)与分子动力学(Molecular Mechanics，MM)相结合的方法，对生物大分子体系中需要仔细观察的重点部位中所包含的少数的原子使用QM方法进行精确的计算，而体系中剩余的部分采用MM方法进行计算．这种方法提高计算结果的精确性，同时可以有效地降低计算成本，因此正被更多的科研人员所采用．

1 量子力学(Quantum Mechanics，QM)方法概述

量子力学的方法是以分子中电子的非定域化为基础，电子的运动使用函数描述，依据海森伯的测不准原理，计算在非定域区间内电子出现的几率．量子力学方法中最为普遍的计算方法为从头算方法，而所谓的从头算方法又被称为分子轨域计算方法，指仅仅采用了分子轨道理论的三个基本近似，在此基础上应用变分原理求解分子的Roothaan-Hall方程的方法，把描述体系电子状态的波函数展开为原子轨域波函数的线性组合．原子轨域的波函数却为某些特定数学函数(如高斯函数等)的线性组合．在核运动和电子运动分离的近似条件下，可以得到多原子分子体系的电子的哈密顿量表达式如下:

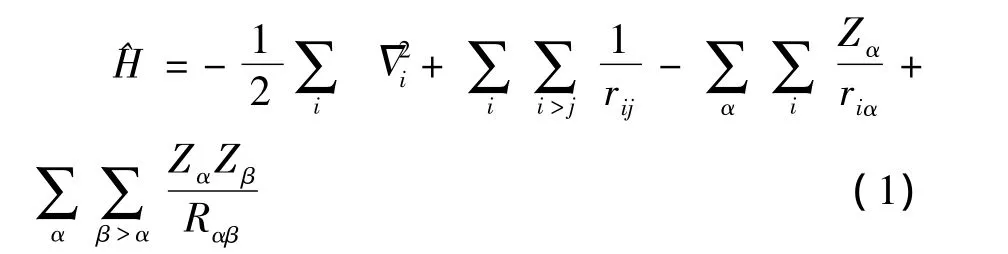
则其薛定谔方程为:

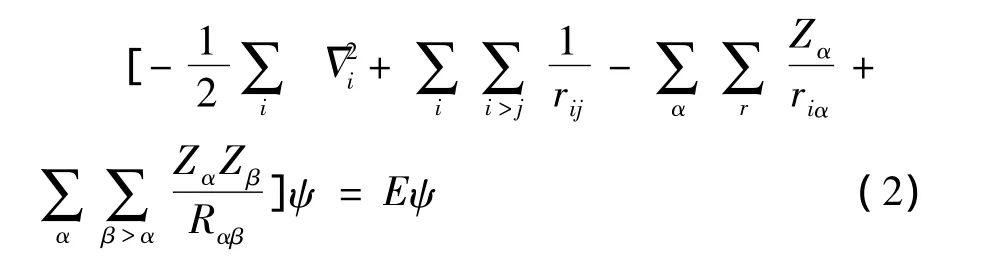
上式都采用原子单位，角标α与β表示的是原子核，i与j表示的是电子．从头算方法十分精确，但是计算速度特别缓慢，导致能计算系统的尺度极其有限，最多不会超过100个原子［1］．为了增加量子力学方法计算的效益，自1960年起，引进了一些实验值作为参数，去替代某些积分项，这种方法被称作半经验分子轨道方法，但还是无法对大体系进行计算．

2 分子动力学(Molecular Mechanics，MM)方法概述

分子动力学理论基本的原理是在一个由N个粒子组成的系统中的每个粒子的运动都遵循Newton方程［2］;通过对每一粒子和其周围的粒子间相互作用势的叠加求得粒子间相互作用势［3］．此方法先使用各粒子的位置坐标计算出系统势能，再由公式(3)、(4)计算出系统中各个粒子受到的力以及其加速度．

只要给出其初始条件，求解体系里各个粒子运动方程获取每一个粒子在不同时刻的运动轨迹，就能够凭借统计学方法去了解体系的状态随时间变化的规律．

分子动力学方法由于使用了保守力场，而它是原子位置坐标的函数，这表明了电子的运动没有被考虑，则电子迁移的过程和电子激发态无法被处理，因此也就不可能去描述化学键的断裂和生成了．

3 QM/MM方法的实现

将量子力学方法与分子动力学方法有机的结合起来，可以有效地避免它们各自缺点，发挥其优点．由此在上世纪70年代发展了QM/MM方法，而其实现的基本原理为ONIOM方法．

3．1 ONIOM方法的基本思想

Morokuma等人提出了ONIOM(Our own nlayered integrated molecular orbital and molecular mechanics)方法［4］，其基本思想是将体系按照其重要性的不同划分成了若干层，每层需要使用不同等级的算法，实现了用多级算法进行模拟计算大体系，这样把大体系给层层分割了．下面以三层ONIOM体系来进行分析．

如图1体系被分成了三层，分别为第一层活跃区，第二层较活跃区及第三层不活跃区．然后再定义三个新体系．即“内核”体系只包含第一层，“媒介”体系包含了第一层和第二层，而“实际”体系包含了全部三层，可采用三种层级算法．例如，“实际”体系可采用经典的分子动力学方法(低层级算法)，“媒介”体系可采用半经验量子化学方法(中层级算法)，“内核”体系可采用最精确的从头算量子化学方法(高层级算法)．

图1 三层ONIOM方法的示意图

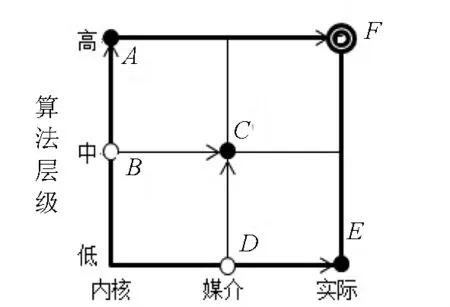
图2 三层ONIOM算法的示意图

图2上的各点代表采用不同的层级算法计算得到对应的体系能量，而F点是采用高层级算法计算得到的“实际”体系能量EF．如果直接使用量子力学方法去计算EF是特别困难的，而ONIOM方法是通过计算A至E五点的能量后近似地获得EF，即

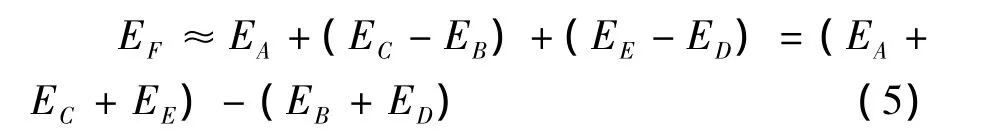
可以看出(EC-EB)和(EE-ED)实际上就是上面定义第二层和第三层能量．计算相邻两个体系的能量差表示各对应层能量是为了保证体系结构的完整性．因此对于被分成n层后的体系使用n个不同层级算法可以得到体系的总能量如下:

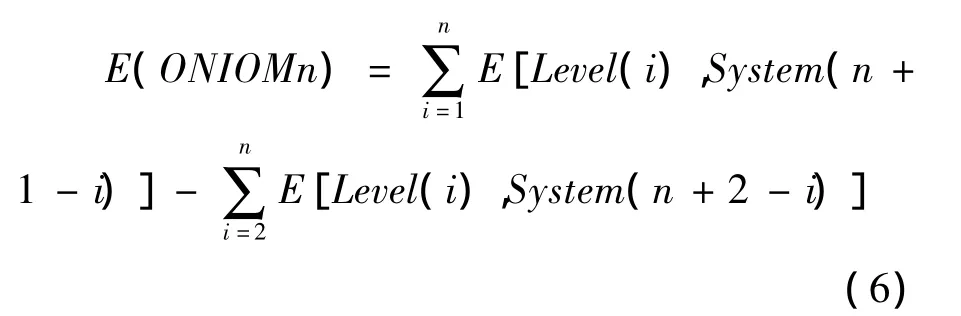
其中E［Level(i)，Model(j)］表示使用第i层级算法计算第j个体系得到的该体系能量．Level(1)为最高层级的算法，Model(1)为包含了所有粒子的“实际”体系．E(ONIOMn)的实质为使用n种层级算法得到了E［Level1(1)，Model(1)］的近似值．

3．2 QM/MM体系的建立

该文中使用双层的ONIOM方法作为例子介绍了QM/MM方法体系的建立．如图3所示，将体系划分为层Ⅰ和层Ⅱ．

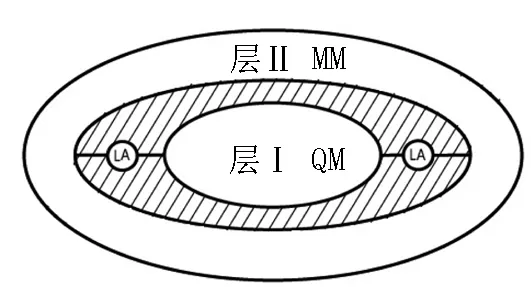
图3 体系分层示意图

图3的层Ⅰ与层Ⅱ是通过加入了链接原子(Link Atom，LA)相连．那么对“实际”体系使用了次层级算法分子动力学(MM)去计算，而对层Ⅰ构成的“内核”体系使用高层级算法量子力学(QM)去计算．显然QM/MM算法得到体系的总能量为［5］

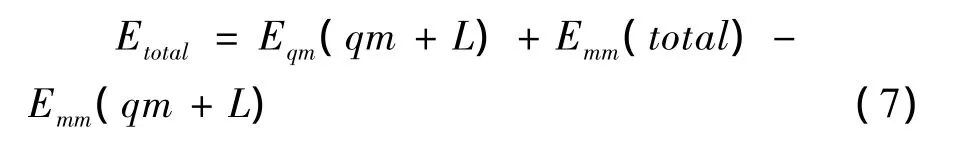
式(7)中的Eqm［6］ 和 Emm

［7］分别为

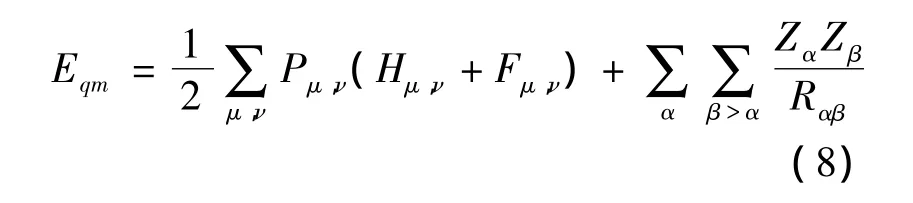
Pμν为密度矩阵元，Hμν为单电子对应原子轨道的哈密顿量矩阵元，Fμ，ν为Fock矩阵元，为核的排斥能．且

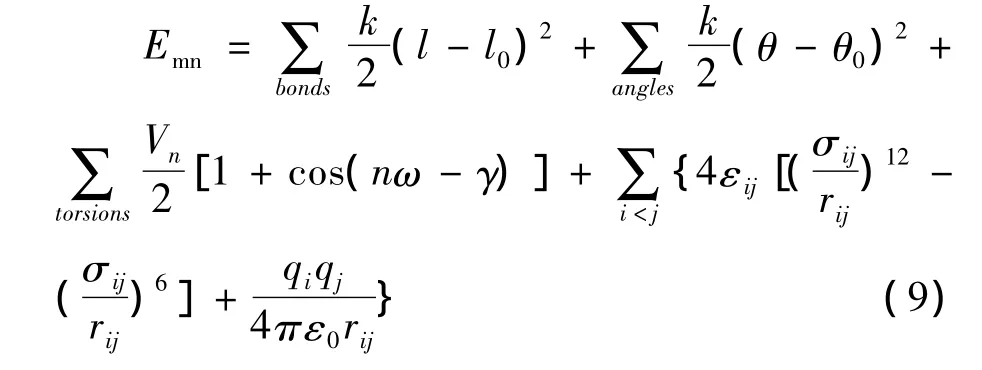
用MOPAC软件［8］中的AM1半经验量子化学方法［9］，选用的是STO-3G基组计算QM区域量子化学能量Eqm(qm+L)，使用GROMACS软件［10］选用OPLS全原子力场去计算QM区域的能量Emm(qm+L)及QM和MM两区域的总能量Emm(total)．

3．3 层边界的处理

如何处理层边界，不同的模拟软件采用不同的方法．在GROMACS软件中是把两层边界的化学键人为断开，将两端组成该化学键的原子分别划归为层Ⅰ与层Ⅱ后再加入一个通常都是虚拟的氢原子的链接原子．链接原子的质量和所带电量都为零，因此对计算的最终结果没影响，而在计算模拟的时候，把它放到使用量子力学计算的层Ⅰ中，链接原子放在断开的成键的两个原子之间，并且这三个原子在一条直线上．例如在OPLASS力场中，断开了键长为0．153 nm的C—C键，用“虚拟的氢原子”来作链接原子，C—H键长为0．108 nm，则链接原子与层Ⅰ的碳原子之间的距离就是0．108 nm，而链接原子与层Ⅱ的碳原子之间距离为0．045 nm，通常令链接原子靠近层Ⅱ那端的原子，两个碳原子的坐标分 别 为 (x1，y1，z1) 和 (x2，y2，z2)，C—H 键 和C—C 键的键长之比是0．108/0．153=0．706．那么链接原子坐标是(x0，y0，z0)，分别为:x0=x1+|x1-x2|× 0．706，y0=y1+|y1-y2|× 0．706，z0=z1+|z1-z2|×0．706，其中角标为1的是层Ⅰ的碳原子，角标为2的是层Ⅱ的碳原子．

4 结束语

目前，QM/MM方法已经用于溶液体系中的化学变化、生物大分子的处理、酶催化原理等方面，得到了很好的发展．在未来的科研工作中，该方法会越来越受到重视．

［1］ 陈光巨，黄元河．量子化学．上海:华东理工大学出版社．

［2］ Alder B J，Wainwright T E．Phase transition for a hardsphere system［J］．J Chem Phys，1957，27:1208-1209．

［3］ 徐筱杰，侯廷军，乔学斌，等．计算机辅助药物分子设计［M］．北京:化学工业出版社．

［4］ Morokuma K，Svensson M，Humbel S，et al．ONIOM:A Multilayered Integrated MO+MM Method for Geometry Optimizations and Single Point Energy Predictions［J］．J Phys Chem，1996，100:19357-19363．

［5］ Obara S，Saika A．Efficient recursive computation of molecular integrals over Cartesian Gaussian functions［J］．J Chem Phys，1986，84，7(1):3963-3974．

［6］ 徐光宪，黎乐民，王德民．量子化学:中册［M］．北京:科学出版社，2009．

［7］ William L，Jorgensen，David S．Maxwell，Julian Tirado-Rives．Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids［J］．J Am Chem Soc，1996，118，11225-11236．

［8］ Dewar M J S．Development and status of MINDO/3 and MNDO［J］．J Mol Struct，1983，100:41．

［9］ Hess B，Bekker H，Berendsen H J C，et al．LINCS:A linear constraint solver for molecular simulations［J］．J Comp Chem，1997，18:1463-1472．

［10］ Bussi G，Donadio D，Parrinello M．Canonical sampling through velocity rescaling［J］．J Chem Phys，2007，126:014101-014101-7．