高阶张量Pareto-特征值的估计

(杭州电子科技大学理学院，浙江 杭州310018)

0 引 言

特征值互补问题在科学工程领域有广泛应用，如机械结构系统、电路仿真、信号处理等问题都可转化成特征值互补问题并求解。众所周知，张量特征值互补问题与其特征值问题关系密切，而后者不可以在多项式时间内求得。著名的Gerschgorin型(圆盘)定理刻划矩阵的特征值估计，在数值分析中有重要应用。张量特征值是2005年提出的新概念[1]，张量特征值互补问题是矩阵特征值互补问题和张量特征值问题的推广，也与一类非线性的微分包含问题密切相关，引起了广泛关注[2]。与矩阵特征值问题不同，张量特征值计算是NP-难问题，张量特征值及其个数计算远比矩阵情形复杂。但与矩阵类型相似，张量特征值或Pareto-特征值可以判别高次多项式的正定性且实际应用广泛。本文给出张量特征值互补问题中的Pareto-特征值的估计，它们是矩阵情形相应结果(如圆盘定理)的张量推广，有重要理论意义和潜在应用价值。

1 问题及相关预备知识

本文考虑张量特征值互补问题(简记TEiCP)，即求λ ∈R和x ∈Rn+{0}，使得:

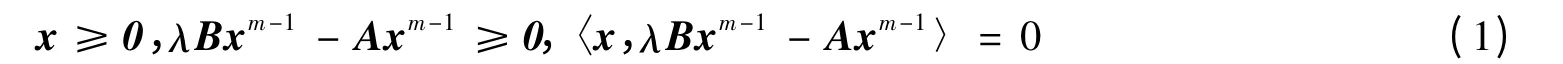
定义1 设A为m阶n维张量。若A的任意元ai1i2…im在下标任意置换下均保持不变，则称A是对称的。

定义2[3]设A为m阶n维张量。若存在非空集I ⊂N:= {1，2，…，n}，使得对任意i1∈I和i2，…，im∉I，均有ai1i2…im=0，则称A为可约，否则称A为不可约。

定义3 设A为m阶n维张量。若A 中任意元素均非负，则称A是非负。若对任意x ∈Rn+{ 0}，均有，则称A为协正定(严格协正定)。

定义4[4]设A为m阶n维张量。若存在满足η≥ρ(C)(η ＞ρ(C))的正实数η和非负张量C，使得A=ηⅠ-C，则称A是M-张量(强-M-张量)。

定义5[5]设A为m阶n维张量。若从Axm-1≥0可推出x ≥0，则称A是单调张量。

命题1[6]设和是m阶n维张量。则λ∈R是张量对(A，B)的Pareto-特征值，当且仅当存在非空集J⊆N和向量使得:

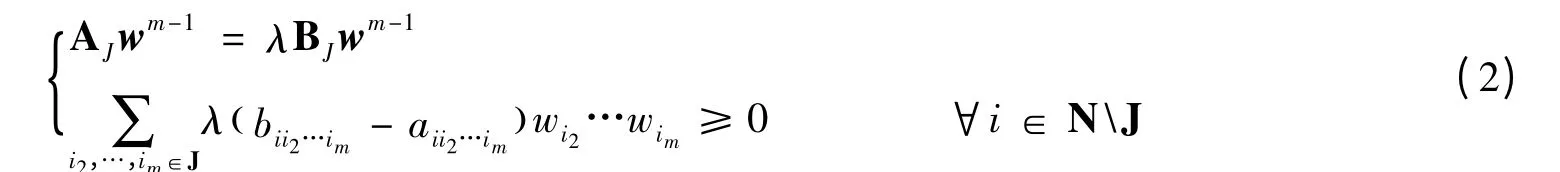
针对满足式(2)的w，定义n维向量x(若i∈J，取xi=wi;否则取xi=0)。易知，x是(A，B)对应于λ的Pareto-特征向量。特别地，若x∈Rn++(即J=N)，则λ 即为(A，B)的特征值。当B =Ⅰ时，λ 被简称为A的Pareto-特征值，其全体记作σP(A)。其中，Ⅰ=(δi1…im)1≤i1，…，im≤n表示单位张量，即δi1…im=1，若i1=…=im;否则 δi1…im=0。此时，式(1)中，Bxm-1变成 x[m-1]，相 应的式(2)变成。其中，x[m-1]表示其分量为的n维向量。

2 Pareto-特征值的估计

张量特征值互补问题与一类高次齐次多项式优化问题关系密切，即使在对称张量的情形下，求解张量特征值互补问题也是一个困难任务。本节关注于Pareto-特征值的估计问题。

定理1 设A=(ai1i2…im)1≤i1，i2，…，im≤n是m阶n维张量，则任意λ ∈σP(A)，有:

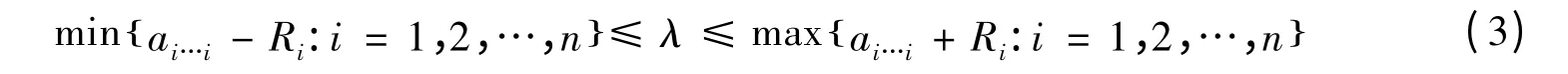
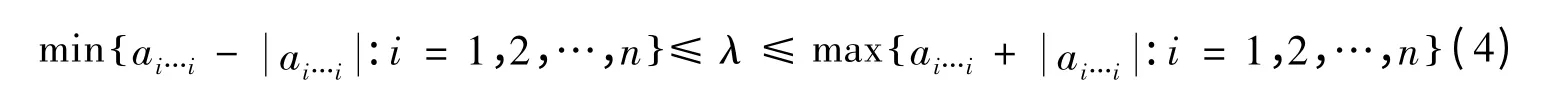
证明 因为λ ∈σP(A)，由命题1 知，存在非空集J ⊆N和，使得:

记wi0=max {wi:i ∈J} 。由式(5)知由此，即得式(3)。特别地，若A 对角占优，则有从而式(4)成立。定理1 证毕。

当m=2时，易知，上述定理即为矩阵特征值互补问题的圆盘定理。关于一般的特征值互补问题Ax =λBx(其中λ ∈C(复数域)，x ∈Cn{ 0})，若A，B是严格对角占优矩阵，则有下面的定理表明，关于张量特征值互补问题也有类似结论。

定理2 设A，B为非零的m阶n维张量。若A 对角占优且B是不可约的，则对任意λ ∈σP(A，B)，有

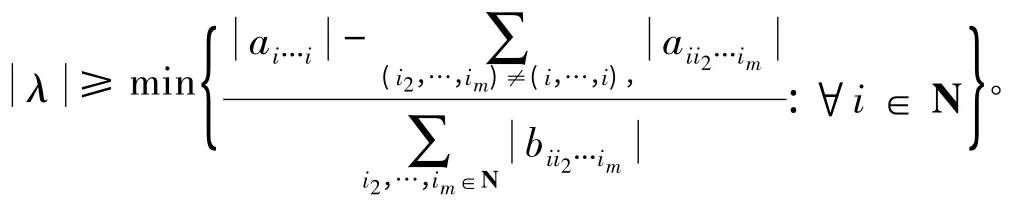
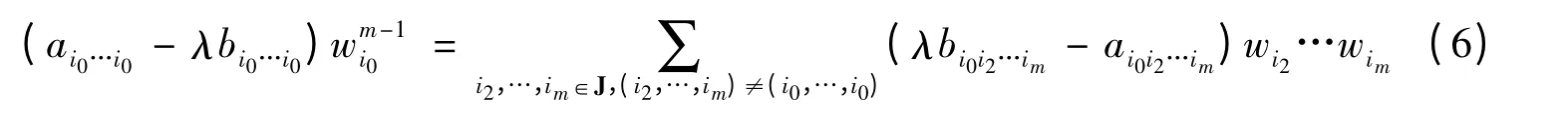
定理3 设A，B是m阶n维张量，其中B 非负且严格协正定。若A 满足条件bi1…im=0⇒ai1…im≤0，则对任意λ ∈σP(A，B)，有其中

证明 记x为对应于λ的Pareto-特征向量。由于B 非负且严格协正定，得Bxm＞0和bii…i＞0。从而由式(1)知，有:

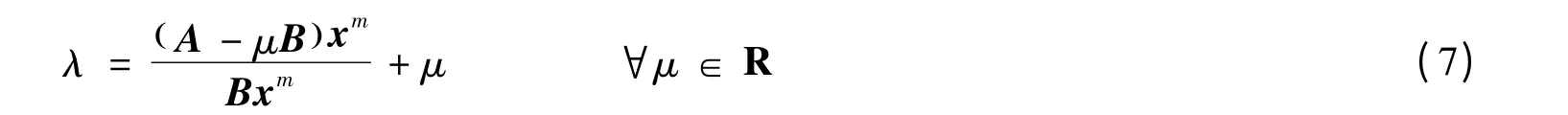
如果m=2，则考虑问题退化成矩阵情形，但所得结论仍然是新的。

3 两类特殊张量Pareto-特征值的非负性

张量Pareto-特征值的非负性有许多实际应用。针对M-张量及单调张量，本文有如下定理，它们分别是矩阵情形相应结论的推广。

定理4 设A，B为m阶n维张量。若A是对称的M-张量，B是严格协正定的，则任意λ∈σP(A，B)都是非负的。进一步，若A是对称的强M-张量，则任意λ∈σP(A，B)都是正的。

证明 设λ∈σP(A，B)，x是相应Pareto-特征向量。因A是M-张量(强-M-张量)，则存在满足η ≥ρ(C)(η ＞ρ(C))的正实数η和非负张量C，使得A=ηⅠ-C。从而，有又由于B为严格协正定，知Bxm＞0(∀x ≠0)。进一步，得:

因A是对称的，从而C是对称的。易知，求解C的谱半径ρ(C)(即最大的H-特征值)等价于求解优化问题[8]所以，有:

由此和式(8)知λ ≥0(λ ＞0)。定理4 证毕。

已知，对称的Z-张量A是强-M-张量，当且仅当A是严格协正定的[9]。从而，由定理4 知，严格协正定对称Z-张量的Pareto-特征值均为正。下面的定理是矩阵相应结论的推广。

定理5 设A，B为m阶n维张量。若m为偶数，A是单调张量且B是非负的，则任意λ∈σP(A，B)都是正的。

证明 设λ∈σP(A，B)。x是相应的Pareto-特征向量。由命题1 知，存在J⊆N和使显然，由于A是单调张量，AJ也是单调张量。若λ≤0，则因m为偶数且B 非负，知由单调张量的定义知，-w≥0。这与矛盾。所以任意Pareto-特征值都是正的。定理5 证毕。

4 结束语

由于张量特征值互补问题的求解是NP-难问题，本文给出若干张量Pareto-特征值的估计式，并证明强M-张量和单调张量的Pareto-特征值均为正。进一步的估计性质将是下一步研究的内容。

[1]Qi L Q.Eigenvalues of a real supersymmetric tensor[J].Journal of Symbolic Computation，2005，40(6):1302-1324.

[2]Song Y S，Qi L Q.Eigenvalue analysis of constrained minimization problem for homogeneous polynomial[EB/OL].[2013-03-16].http://arxiv.org/abs/1302.6085v2.

[3]Chang K C，Pearson K，Zhang T.Perron Frobenius theorem for nonnegative tensors[J].Communications in Mathematical Sciences，2008，6(2):507-520.

[4]Zhang L P，Qi L Q，Zhou G L.M-tensors and some applications[J].SIAM Journal on Matrix Analysis and Applications，2014，35(2):437-452.

[5]Ding W，Qi L Q，Wei Y.M-tensor and nonsingular M-tensors[J].Linear Algebra and its Applications，2013，439(10):3264-3278.

[6]Adly S，Rammal H.A new method for solving Pareto eigenvalue complementarity problems[J].Computational Optimization and Applications，2013，55(3):703-731.

[7]刘裔宏.关于广义特征值估计的一个Gerschgorin 定理[J].工科数学，1994，10(1):49-51.

[8]Qi L Q.Symmetric nonnegative tensors and copositive tensors[J].Linear Algebra and its Applications，2013，439(1):228-238.

[9]陈景良，陈向晖.特殊矩阵[M].北京:清华大学出版社，2000:276-286.