一种基于遗传算法的关联规则改进算法
2015-12-02
(杭州电子科技大学计算机学院,浙江 杭州3150018)
0 引 言
传统的关联规则挖掘算法采用的“支持度-置信度”度量标准存在一定的不足。第一个问题是生成的规则数量随项集数成指数级增长,其中也包含弱关联规则和误导规则。第二个问题是如何从规则中提取出有效的规则。很多学者通过遗传算法对关联规则算法进行改进以解决上述问题。文献[1]提出了一种基于遗传算法和模糊集的关联规则算法进行web 挖掘。为了提高规则的精确度,文献[2]用遗传算法来找到所有潜在的优化规则,文献[3]提出了一种新的遗传算子SSOCF,该算子能够使数据集中的有效信息一直被遗传下去。本文利用遗传算法对Apriori算法进行改进,使用多个度量标准构成适应度函数来综合度量规则的有效性。
1 基于遗传算法的关联规则
1.1 关联规则
一个关联规则是形如X→Y的蕴涵式,其中X 称为规则前件,Y 称为规则后件,且X和Y 都是事务数据库中的频繁项集,X∩Y=Φ。规则的置信度和支持度是度量规则有效性的两个重要标准。大部分关联规则挖掘的任务就是提取出满足这两个阈值的所有规则。
1.2 遗传算法
遗传算法(Genetic Algorithm,GA)中包含了编码、适应度函数和遗传算子。由于GA是一种全局优化算法,避免了搜索过程中局部最优,因此应用遗传算法进行关联规则挖掘能够得到较好的关联规则,且复杂度低于其他的关联规则算法[4]。遗传算法的终止条件有:遗传代数达到最大遗传代数,或者最优个体适应度达到给定的阀值,或者最优个体的适应值和群体适应度不再上升等。
1.3 GA-Apriori算法
Apriori算法是经典的关联规则算法,Apriori算法的设计分解为2个步骤:
1)根据支持度阈值从事务数据库中挖掘出所有频繁项集;
2)基于第1步挖掘到的频繁项集,根据置信度阈值产生全部的关联规则。
本文应用遗传算法对Apriori算法进行改进优化,提出了一种叫做GA-Apriori的算法。
1.3.1 编码
本文应用Michigan的编码方式[4],即一条染色体代表一个规则。假设要挖掘的数据集中有n个属性,规则分为前件和后件两部分。第一个基因代表第一个属性值。染色体中前i个基因代表规则前件部分的属性,后(n-i)个基因代表规则后件部分的属性。
例如脊椎动物数据集,属性如表1所示。

表1 脊柱动物数据集
假设有一个规则:体温=恒温,胎生=是→类别=哺乳类,则染色体编码将为“11##1”,编码为“#”表示规则中没有出现该属性。
1.3.2 适应度函数
适应度函数是一种特殊的目标函数,该函数用于评价个体的优劣程度。一条规则是否有效,要从有用性、确定性、简洁性和新奇性综合度量。因此本文考虑4个度量标准,分别为支持度、置信度、理解度和兴趣度,并与用户定义的权重相结合转化为适应度函数。对于规则X →Y:
支持度是指在事务数据库中包含X ∪Y的事务占整个事务的比例,记为:

式中,σ(N)表示事务的总数,σ(X ∪Y)表示同时包含X和Y的事务数。
置信度是指在事务数据库中包含X ∪Y的事务与含有项集X的事务的比:

式中,σ(X)表示包含X的事务数。置信度值高表示X和Y的关联程度越大。
理解度是度量规则简洁性的标准,规则长度过长,即包含了大量属性的关联规则不利于用户理解。规则越长,用户理解规则也就越困难,关联规则中的理解度定义为:

式中,|Y|表示后件包含的属性数量,|X ∪Y|表示规则中属性的总数量。
兴趣度体现了规则的新奇性,由于关联规则挖掘是要找到一些隐藏的信息,也就是应该发现那些在数据库中发生相对较少的规则。文献[5]中规则的兴趣度定义为:
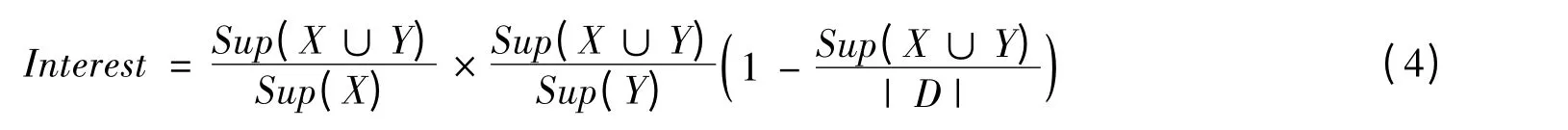
式中,Sup(X ∪Y)/Sup(X)表示根据前件产生规则的概率,Sup(X ∪Y)/Sup(Y)表示根据后件产生规则的概率,Sup(X ∪Y)/|D|表示根据整个数据集包含规则的概率,[1-Sup(X ∪Y)/|D|]表示不包含规则的概率。式中得知具有较高支持度的规则可能具有较低的兴趣度。
根据以上描述,本文定义一条规则的适应度函数为:

式中,W1,W2,W3,W4是用户根据需要定义的权重,从而对规则评价的侧重方面可以发生变化。权值越大,表示该度量标准越重要。
1.3.3 遗传算子
遗传算子是遗传算法中重要的组成部分,包括选择算子,交叉算子和变异算子。
1)选择算子。选择操作的作用就是将环境适应性好的个体遗传到后代。根据个体适应度函数值的大小通过某种方法将个体从父代个体中挑选出来,然后进入下一代,选择算子设计依赖概率,个体Xi选择概率定义为:
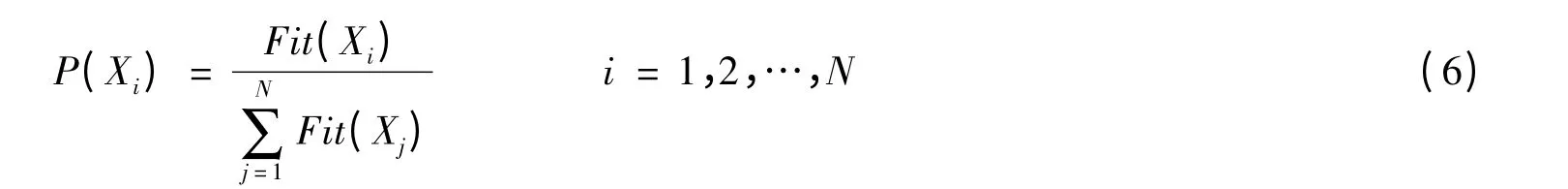
本文选用基于赌轮法的选择算子。根据个体的排序,按照选择概率P(Xi)计算累计概率qi=则P(Xi)= qi-qi-1。产生N个随机数pk,对每一个pk,若qi-1<pk<qi则复制Xi,可以得到选择复制后的N个新一代个体。
2)交叉算子。交叉是把两个父代个体的部分结构加以重组而生成新个体的操作。本文采用单点交叉的方法并且交叉概率Pc=0.95。在基因串中随机设定一个交叉点。实行交叉时,该点前或者后的两个个体的部分结构互换,并生成两个新个体。设双亲为:x=(x1,x2,…,xn),y=(y1,y2,…yn),在随机的第K位交叉,生成的后代为x=(x1,x2,…xk,yk+1,yk+2,…yn),y=(y1,y2,…yk,xk+1,xk+2,…xn)。
3)变异算子。变异是对群体中的个体的某些基因值的改变。变异的作用是使种群中的某些个体的基因(位)产生突变从而引入原种群不包含的基因,形成新个体。本文采用基本变异算子,在群体中染色体随机挑选C个基因位置并对这些基因值以变异概率Pm取反,即0 变成1,1 变成0。
1.3.4 算法流程
GA-Apriori算法通过Apriori算法第一步得到频繁项集,然后对所有频繁项集进行编码,通过选择、交叉、变异操作得到关联规则集。Apriori算法中得到频繁项集的流程如图1所示,GA-Apriori算法的流程如图2所示。
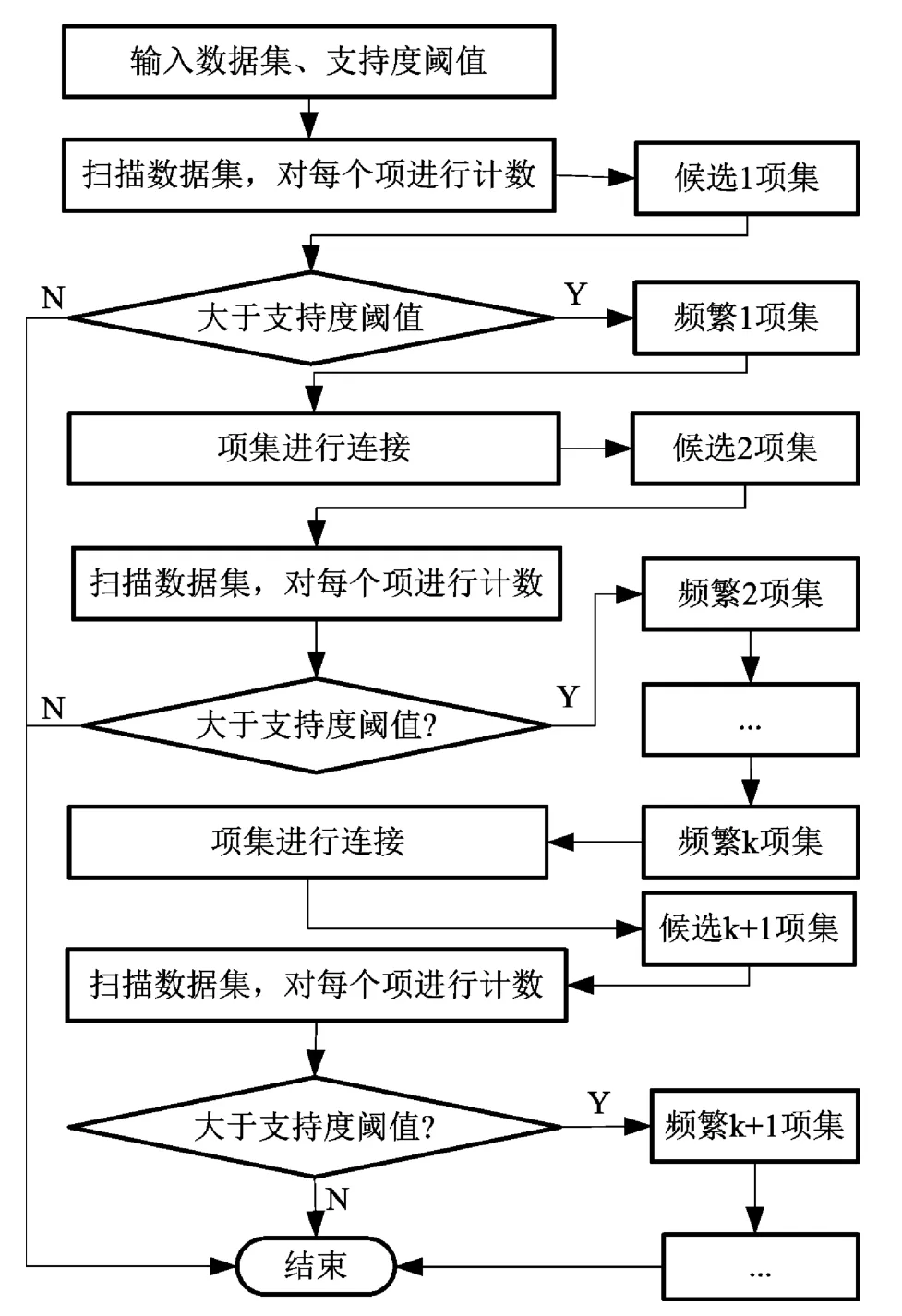
图1 Apriori算法产生频繁项集的流程图
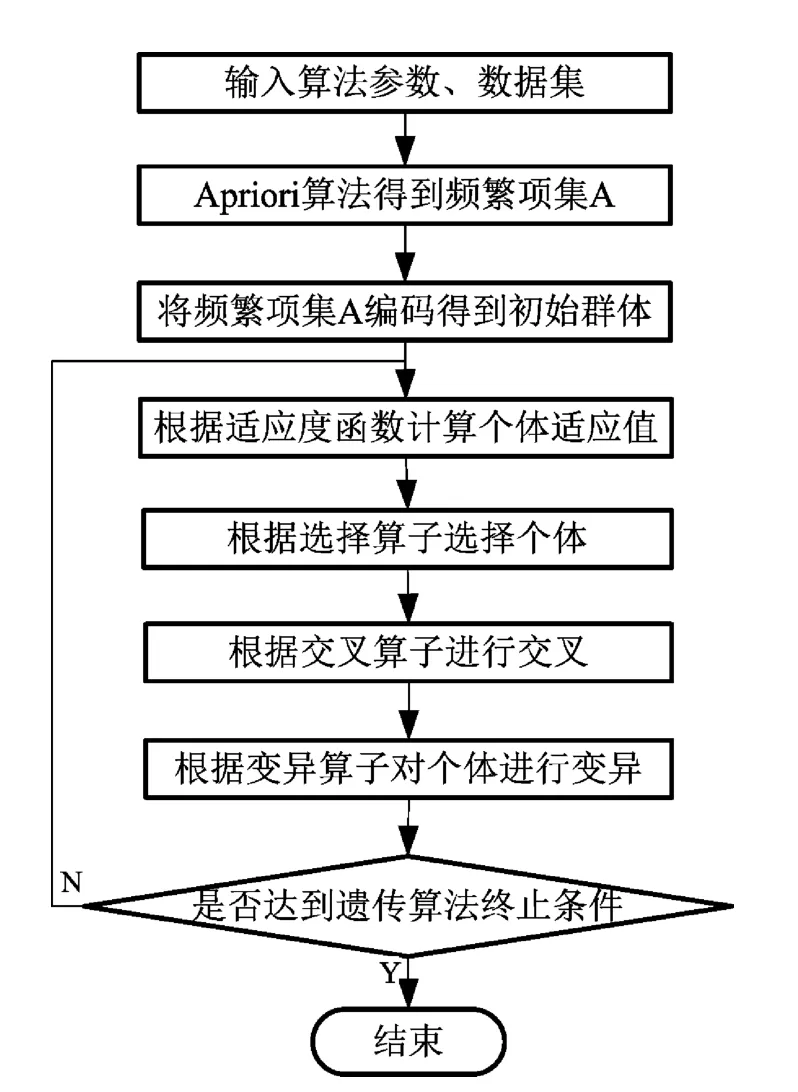
图2 GA-Apriori算法流程图
2 实验结果与分析
本文对加州大学欧文分校(University of California Irvine)提出的UCI数据库中的3个数据集进行测试。遗传算法中含有个体数量为100,遗传代数为200,交叉算子Pc=0.95,变异算子Pm=0.001,结合支持度、置信度、理解度和兴趣度的重要程度,因此本文定义的权重为W1=4,W2=3,W3=2和W4=1。将GA-Apriori算法与Apriori算法得出的结果进行比较分析。测试数据库特性如表2所示,在相同支持度和置信度条件下得到的规则数量如图3、图4所示,规则的平均支持度和平均置信度如图5、图6所示。
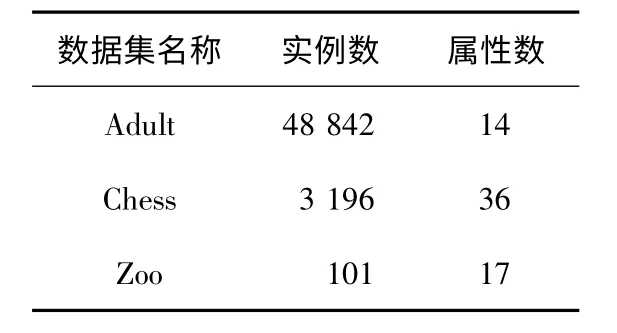
表2 测试数据库特性
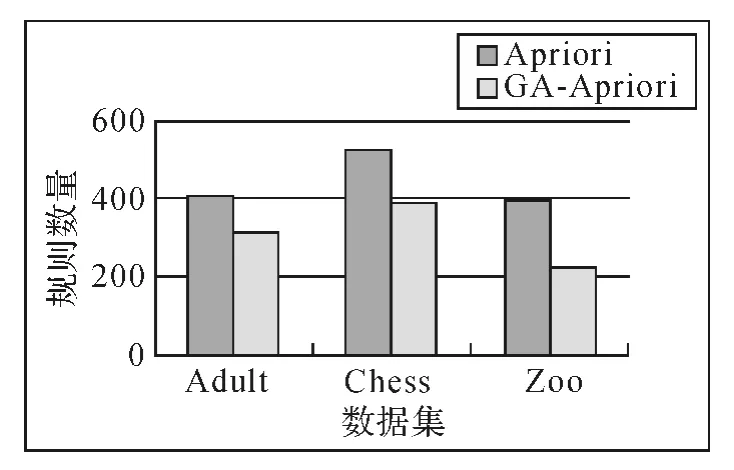
图3 Sup=0.1,Con=0.5时关联规则数量比较
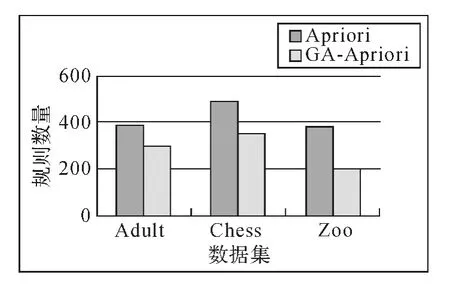
图4 Sup=0.2,Con=0.5时关联规则数量比较

图5 算法平均支持度比较

图6 算法平均置信度比较
由图3、图4得知,在相同支持度和置信度阈值下GA-Apriori算法得到规则数量少于Apriori算法,由图5、图6得知GA-Apriori算法得到的规则平均支持度和平均置信度均高于Apriori算法。通过实验分析可知本文提出的算法GA-Apriori算法能够有效减少规则数量,关联规则的精准率也高于Apriori算法。
3 结束语
本文使用遗传算法对Apriori算法进行改进优化,综合考虑多个度量标准,并对规则的有效性进行分析,有效地减少了基于“支持度-置信度”度量标准算法中的不足,有效减少了关联规则的数量,其中包括一些弱关联规则和误导关联规则。
[1]Chai C,Li B.A Novel Association Rules Method Based on Genetic Algorithm and Fuzzy Set Strategy for Web Mining[J].Journal of Computers,2010,5(9):1448-1455.
[2]Anandhavalli M,Sudhanshu S K,Kumar A,et al.Optimized Association Rule Mining Using Genetic Algorithm[J].Advances in Information Mining,2009,1(2):1-4.
[3]Soto W,Olaya-Benavides A.A Genetic Algorithm for Discovery of Association Rules[C]//Proceedings of the 2011 30th International Conference of the Chilean Computer Science Society.IEEE Computer Society,2011:289-293.
[4]Yan X,Zhang C,Zhang S.Genetic Algorithm-Based Strategy for Identifying Association Rules without Specifying Actual Minimum Support[J].Expert Systems with Applications,2009,36(2):3066-3076.
[5]Qodmanan H R,Nasiri M,Minaei-Bidgoli B.Multi objective association rule mining with genetic algorithm without specifying minimum support and minimum confidence[J].Expert Systems with Applications,2011,38(1):288-298.
