电力亚式期权定价模型的奇摄动解

(杭州电子科技大学理学院，浙江 杭州310018)

0 引 言

一直以来，电力衍生产品在电力市场发展过程中有着重要的需求，电力衍生产品的定价问题受到广泛关注。近年来人们根据奇异期权中路径依赖型期权的思想，设计研究出电力亚式期权，并运用二叉树模型进行估值[1]，得出了这种期权的定价方式，但由于市场机制、国家监管、信息共享等制度的不完善，二叉树每个结点上的数据和估值缺乏准确度。因此对电力亚式期权定价进行渐近分析就显得尤为必要。考虑到电力衍生产品的随机波动和现实电力市场存在一定的差距，本文讨论了一类电力亚式期权定价随机波动率模型，波动率采用快速均值回归的随机波动率模型，通过运用奇摄动渐近展开的方法，求得了电力亚式期权定价所因满足的Black-Sholes 方程及其渐近解，并得到了误差的一致有效估计。

1 模型建立

考虑亚式期权的随机波动率模型，设风险资产价格为S(t)，满足如下的随机微分方程:

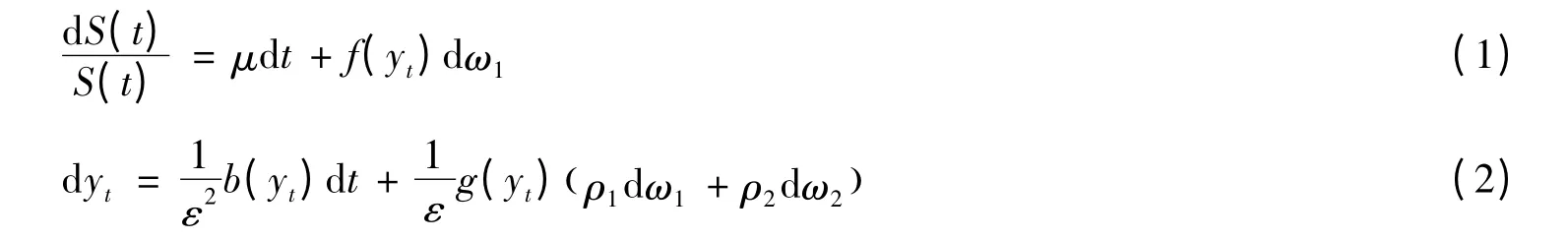
设ρ'T=(ρ1，ρ)2，r为无风险利率，γ(y)为风险期权金因子，r ＞0，所以式(1)、式(2)可改为:

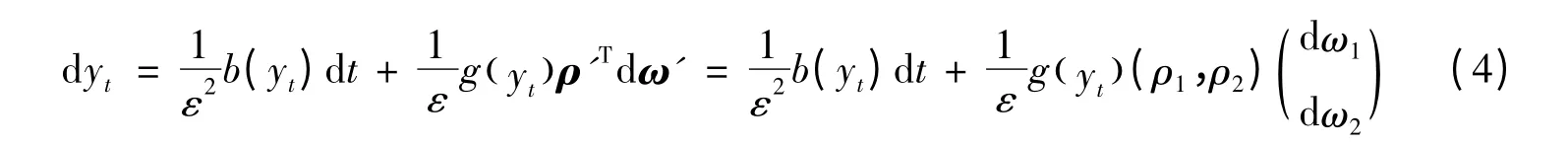
首先假设以下条件:

1)对任一y ∈R，f(y) ≠0;

2)f(y)，γ(y)，b(y)，g(y) 在R 上连续;

引入无风险测度P*[2-3]，令:

将式(5) (7)代入式(3)、式(4)，则式(3)、式(4)可改为:

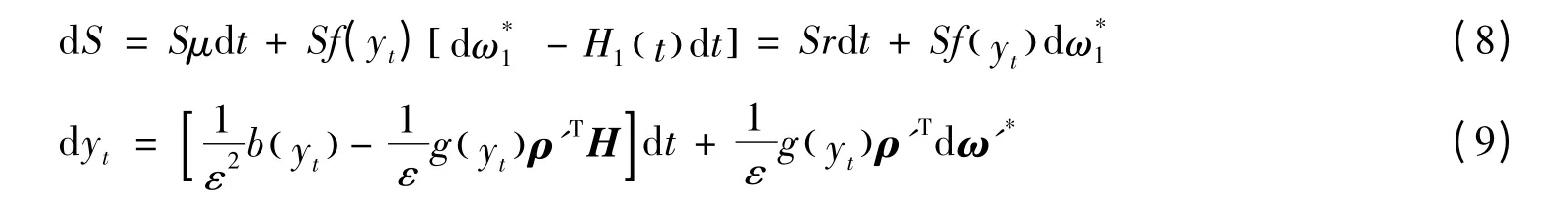
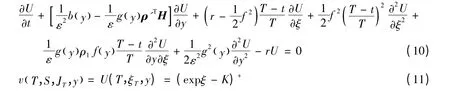
定解区域为D=[0，T]×R2，引入如下算子:

因此有:

2 形式渐近展开

将U(t，ξ，y)，作如下的形式渐近展开式[6]:

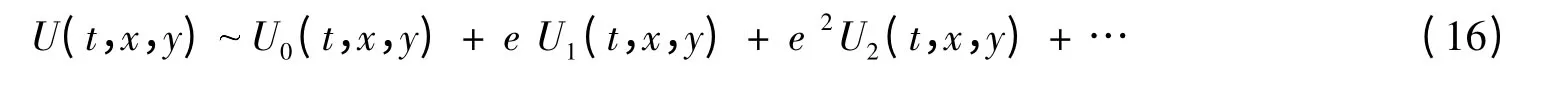
引理1 当条件1～3 满足时，则有L*0P(y)= 0，并有唯一的解P(y)，满足P(y)≥0，y ∈R，L*0是L0的伴随算子，有P(y)在 [-R，R]上Lipshitz 连续。引理1可见文献[7]。

引理2[7]满足条件1～3，L0U0=0，那么U0=U0(t，ξ)与y 无关。

3 一致有效性

对任一紧集Ω ⊆R2，令QT=[0，T]×Ω，则其中M为与ε 无关的正常数。

证明 将式(17)代入式(15)，整理得:

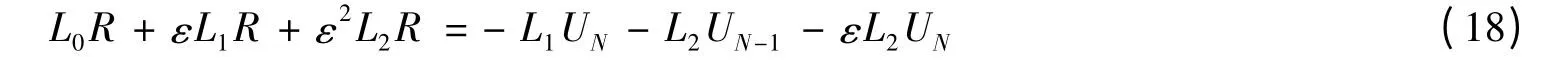
令φ=L1UN+L2UN-1+εL2UN，由条件1-3可知在QT上φ 有界。

当u →0+，有由De Giorgi 迭代技术[9]得到因而进而形式渐近展开式一致有效。定理得证。

4 结束语

本文对于一类电力亚式期权定价模型，波动率采用快速均值回归的随机波动率模型的情形进行了讨论。通过引入无风险测度P*，及测度变换，借助Feynman-Kac 公式得到了电力亚式期权定价Black-Scholes模型;运用奇摄动渐近展开方法得到了电力亚式期权定价的渐近解;并用DeGiorgi 迭代技术证明了渐近解的一致有效性，从而得到了电力亚式期权定价的求解方法。

[1]李江，施泉生.电力奇异期权及其估值研究[J].华东电力，2008，36(6):31-33.

[2]吴恒煜，陈金贤.基于价格随机波动率的衍生产品期权定价[J].西安交通大学学报，2005，39(2):214-217.

[3]Zhu S P，Chen W T.A new analytical approximation for European puts with stochastic volatility[J].Applied Mathematics Letters，2010，23(6)，687-692

[4]林清泉，杨丰.公司债务定价理论与实证:基于条款约束视角[M].北京:中国人民大学出版社，2009:79-81.

[5]姜礼尚.期权定价的数学模型和方法[M].北京:高等教育出版社，2008:288-297.

[6]Fukasawa M.Asymptotic analysis for stochastic volatility:edgeworth expansion[J].Electronic Journal of Probability，2010，16(25):764-791.

[7]包立平.高维欧式期权定价模型的奇摄动解[J].应用数学与计算数学学报，2011，25(2):194-204.

[8]马研生.一类非光滑条件下欧式期权定价模型[J].应用数学学报，2010，33(6):1011-1018.

[9]伍卓群，尹景学，王春明.椭圆与抛物方程引论[M].北京:科学出版社，2003:80-85.