一种基于低秩矩阵逼近的图像去噪算法

诸 亮，周林强，李一啸，黄朝耿

(1.浙江工业大学浙江省信号处理重点实验室，浙江 杭州310023;2.浙江工业大学信息学院，浙江 杭州310023;3.浙江财经大学信息学院 浙江 杭州310018)

0 引 言

图像作为重要的信息来源，在生活中扮演着重要的角色。然而现实中的图像或多或少都存在着噪声的污染，因此图像去噪变得至关重要。文献[1]最早将图像的非局部自相似性(Non-local Selfsimilarity，NSS)应用到图像去噪中，设计了非局部图像去噪算法。非局部图像去噪算法是当前较为新颖的去噪算法，由于更好地保留了图像的细节，得到了进一步的研究和发展[2]。K.Dabov 提出的三维块匹配(BM3D)算法同样基于非局部自相似性，是当前公认的最佳去噪方法。自然图像中往往存在相似图形块，相似块具有相似的结构特征和数据特征，它们组成的矩阵是低秩的。低秩矩阵逼近(Low Rank Matrix Approximation，LRMA)[3]是一种矩阵秩最小问题，可等价为线性约束条件下的核范数最小化(Nuclear Norm Minimization，NNM)[4]问题。文献[5]证明低秩矩阵可以用NNM 近似，NNM 又可通过奇异值的软阈值法(Soft-thresholding operation)实现。本文结合NSS和LRMA 提出了一种新的图像去噪算法。算法的实现分为两步，首先是图像相似块的匹配和分组，其次对图像相似块组成的矩阵进行处理从而达到去噪效果，是一种非常有效、去噪效果好的图像去噪算法。

1 图像去噪算法设计

1.1 算法流程设计

本文的图像去噪算法流程如图1所示。

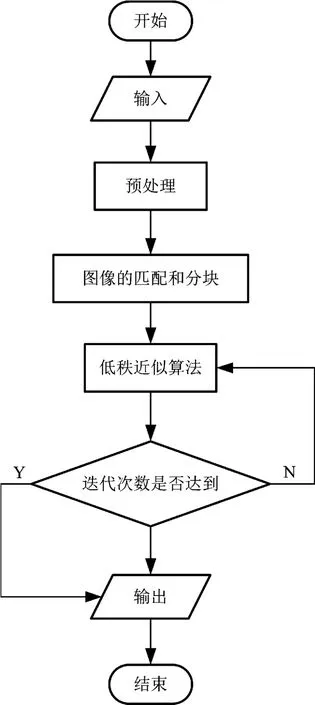
图1 图像去噪算法流程图

输入图像往往是有噪的，直接分块匹配会导致输出结果的不准确，有必要在图像分块匹配前先对有噪图像进行中值滤波的预处理。图像的匹配和分块是以某个像素为中心的一个大小为n×n的图像块p ∈Rn2，寻找与p 相似的非局部的图像块。假设找到m 块这样的图像块，记为然后将每个图像块排成一个列向量组合成一个n2×m的矩阵。低秩矩阵逼近问题可等价于约束条件下的最小化问题，再通过多次迭代得到干净的块矩阵。

1.2 算法设计

传统的噪声图像模型如下:

式中，Y为测量图像，X为原始图像，N为独立同分布的加性高斯白噪声，均值为零，方差为φ2n。

式(1)等价于线性约束下的矩阵核范数最小化问题，目标函数如下:

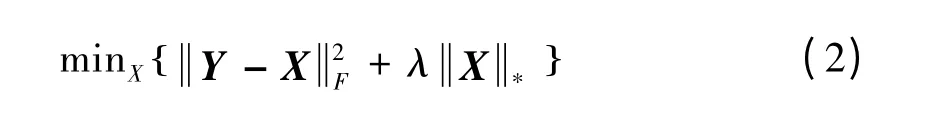
结合NSS，假设ys是噪声图像Y中的一个块，利用块匹配方法在Y 中找出ys的非局部自相似块，将这些非局部自相似块矩阵化，得到一个低秩矩阵，假设为Ys。于是Ys=Xs+Ns，Xs、Ns分别为原始图像和噪声中自相似块的矩阵化，因为Xs是一个低秩矩阵，将式(3)所示的WNNM模型应用于Ys，得到:

假设∀Ys∈Rm×n，Ys=U∑YsVT是其奇异值分解，Ys的秩为M，Xs的秩为N，因为Xs是低秩的，所以N ＜M。式(4)模型的解可以表示为Xs=UBVT，证明如下:

设U⊥是酉矩阵U的正交补，所以Xs=UX1+U⊥X2，这里X1和X2是Xs在空间U和U⊥下的分量，根据Courant-Fisher 极小极大定理[7]得到

因为WNNM模型等价于约束条件小的最小化问题，不等式可以取等，式(4)化简可得:

根据奇异值的物理意义，越大的奇异值对矩阵的作用越大，对应的权重系数ωi应取越小。设定ωi=c/σi(B)，c是一个常数，此时是一个常数，与B 无关，于是式(5)进一步化简为如下式的最优化问题:

式中，B 必须满足低秩条件，设B={ bij}，将式(6)展开如下:

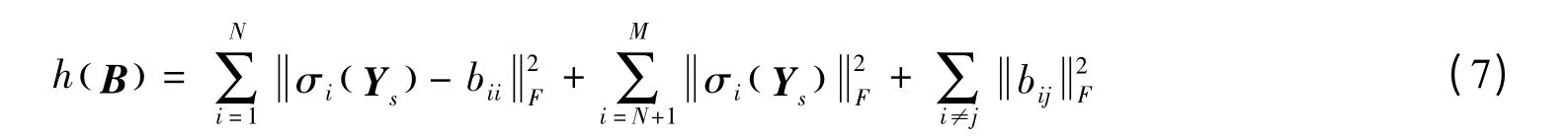
当式(7)中第1 项和第3 项为0时，取得最小值，即当i=1，2，...，N，bii=σi(Ys)，其余 { bij}均为零时，式(6)得到最优解，图像成功去噪。

2 仿真实验

2.1 实验参数设置

实验中，通过多次迭代来加强去噪效果，每次迭代将f (Xs)的最优解重新赋值给Ys进入下一次迭代。设K为迭代次数，另外根据噪声标准差设置图像分块大小和自相似块Xs的秩N，具体如表1所示。

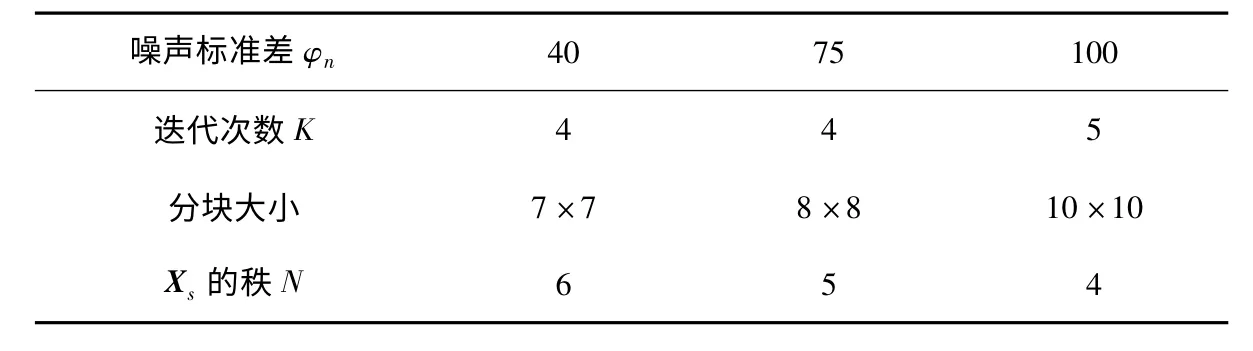
表1 参数设置表

设定3种噪声，φn分别为40，75，100，分别代表较低噪声，中等噪声和强噪声。

2.2 仿真结果

选择同样基于非局部平均的图像去噪算法NCSR、LSSC、EPLL、与本文算法进行对比。用“帝王蝶”图和浙江工业大学图书馆的图片进行算法比较，峰值信噪比(Peak Signal to Noise Ratio，PSNR)作为比较标准，其中“帝王蝶”图的比较结果如表2所示。

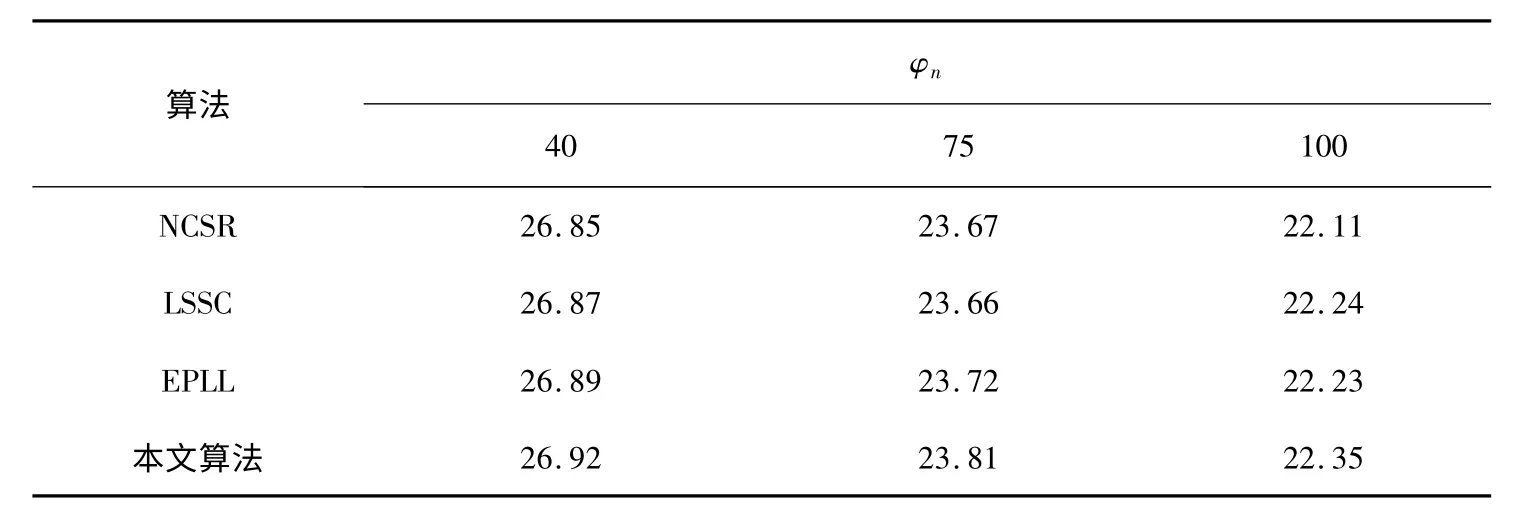
表2 基于“帝王蝶”图的不同算法去噪性能(PSNR)比较表

从表2可以发现本文算法总体上优于其它3种算法。在不同的噪声级别下，本文算法都具有更好的峰值信噪比。当噪声很小时，所有算法都具有很好的PSNR，但当噪声增强时，本文的算法比其它3种算法的优势更大，这说明本文的算法性能更好。再结合表1中的参数设置，可以发现本文算法具有更好的收敛速度，在不同的噪声级别下，本文算法最多只要5次迭代就可以达到最好的去噪输出。

在φn为40的较低噪声环境下，将本文算法与其它3种算法进行比较，选用浙江工业大学图书馆的图片进行视觉比较，比较结果如图2所示。

图2 φn =40时，基于浙江工业大学图书馆图的不同算法的去噪效果比较

图2中图2(a)为原始图像，图2(b)为有噪图像，PSNR =16.06 dB，图2(c)为NCSR 去噪输出，PSNR=28.31 dB，图2(d)为LSSC 去噪输出，PSNR =28.36 dB，图2(e)为EPLL 去噪输出，PSNR =28.43 dB，图2(f)为本文算法的去噪输出，PSNR =28.51 dB。从图2中可以看出，相对于其它3种算法，本文算法具有更好的去噪性能和视觉效果，输出结果更平滑，拥有更好的纹理和边缘区域。为了从视觉上验证当噪声增大时，本文算法具有更好的噪声鲁棒性。

在强噪声环境下选用“帝王蝶”图将本文算法与其它3种算法进行视觉上的比较。φn为100时，比较结果如图3所示。

图3 φn =100时，基于“帝王蝶”图的不同算法的去噪效果比较

图3中图3(a)为原始图像，图3(b)为有噪图像，PSNR=8.10 dB，图3(c)为NCSR 去噪输出，PSNR=22.11 dB，图3(d)为LSSC 去噪输出，PSNR=22.24 dB，图3(e)为EPLL 去噪输出，PSNR=22.23 dB，图2(f)为本文算法的去噪输出，PSNR=22.35 dB。从图3可以在视觉上生动地感受到本文算法优异的去噪性能，即使在φn为100的强噪声下，本文算法依然具有较好的视觉效果。

3 结束语

作为对图像去噪的一种尝试，本文结合非局部自相似性和低秩矩阵逼近提出了一种新的图像去噪算法。实验结果显示本文算法总体上优于NCSR，LSSC，EPLL 经典的图像去噪算法，具有更高的PSNR和更好的去噪输出。但是，与BM3D 相比，本文算法还存在不足，BM3D的收敛速度非常快，而本文算法的收敛性还有待进一步提高。本文只选用一种噪声测试去噪效果，接下来将把算法用于不同噪声的去噪，扩大算法的普适性。

[1]Buades A，Coll B.A non-local algorithm for image denoising[C]//Computer Vision and Pattern Recognition，2005.CVPR 2005.IEEE Computer Society Conference on.IEEE，2005:60-65.

[2]Kervrann C，Boulange R J.Optimal spatial adaptation for patch-based image denoising[J].IEEE Transactions on Image Processing，2006，15(10):2866-2878.

[3]范云鹏.矩阵低秩逼近在图像压缩中的应用[D].西安:西安电子科技大学，2012:26-30.

[4]赵新斌.一类带有核范数的优化问题的梯度算法[D].北京:北京工业大学，2012:13-25.

[5]Candes E J，Recht B.Exact matrix completion via convex optimization[J].Foundations of Computational mathematics，2009，9(6):717-772.

[6]Gu S，Zhang L，Zuo W，et al.Weighted Nuclear Norm Minimization with Application to Image Denoising[C]//Computer Vision and Pattern Recognition(CVPR)，2014 IEEE Conference on.Columbus，OH:IEEE，2014:2862-2869.

[7]张吉慧.关于极小极大原理[J].纯粹数学与应用数学，1999，15(2):1-6.