截断傅里叶变换加密系统的安全性分析

(杭州电子科技大学理学院，浙江 杭州310018)

0 引 言

1995年，美国学者Refregier和Javidi[1]提出双随机相位编码光学加密系统后，光学信息安全技术得到了快速的发展[2-4]。加密系统的线性特性使其存在一定的安全隐患，通过选择明文和已知明文的方法可以恢复出原始图像信息[5-6]。文献[7]提出了基于相位截断傅里叶变换的非对称光学加密系统，利用振幅截断处理产生的两个与加密密钥完全不同的解密密钥来恢复原文。尽管相位截断傅里叶变换破坏了加密系统的线性性质，在一定程度上增强了系统的安全性。但是，文献[8-9]利用迭代傅里叶变换算法恢复了原文信息，说明该系统还是存在一定的安全问题。文献[10]通过一种改进措施来增强相位截断傅里叶变换加密系统的安全性，在原有加密系统的频谱域中加入一个振幅掩膜，有效地抵抗迭代傅里叶变换的攻击。在一种新的攻击下，文献[11]发现这个加密系统的明文还是可以被攻击的，因此该加密系统的安全性还需要进一步提高。针对以上情况，本文经过分析和讨论，提出了一种新的改进措施，对原有的振幅掩膜板分布进行了调整，模拟实验表明，在各种已有的攻击下，改进后的系统都表现出很强的安全性。

1 相位截断傅里叶变换加密系统的安全性增强

相位截断傅里叶变换加密系统的安全性有一定提高，但是，用一种特殊的攻击方法依然可以恢复出原始图像[8]。文献[10]提出在相位截断傅里叶变换加密系统的傅里叶平面加入一个振幅掩膜A1来提高抗攻击能力，其加密流程如图1所示。

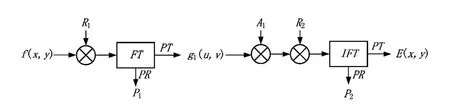
图1 修正后的加密流程图

图1中，A1为一个未公开的随机振幅掩膜，由振幅透过比为1和一个正实数k (k ＜1)随机分布组成的。加密过程表示为:

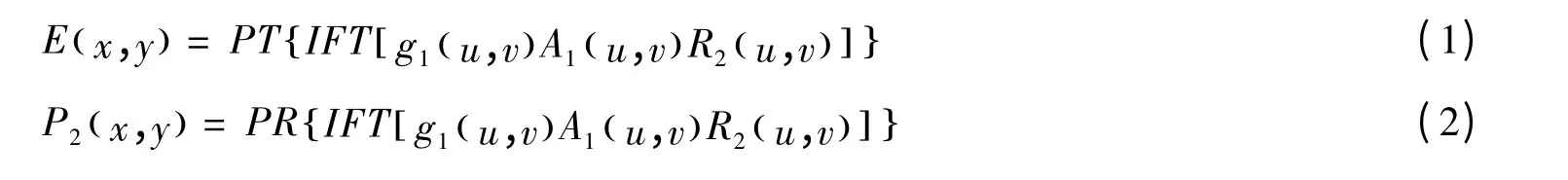
解密过程是加密过程的逆过程:

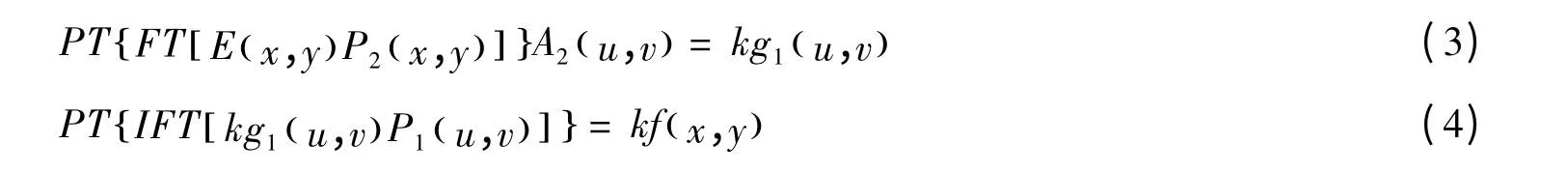
式中，A2(u，v)·A1(u，v)=k，A2(u，v)可以当作一个附加的密钥。这个加密系统对某些攻击的安全性已经得到验证，可见安全性有了一定的提升。

截断傅里叶变换加密系统中，加密密钥被当做公钥，而解密密钥被当做私钥，通过振幅-相位的截取破坏了传统加密系统的线性性质。私钥是在加密的过程中产生的，而且随着明文的改变而改变的。在光学信息加密领域对非对称加密系统的概念还没有一个严格的定义，由于加密解密密钥的不同，本文把相位截断加密系统称作“非对称加密系统”。

2 一种新型的攻击方法

文献[11]提出了一种新型的攻击算法，并且成功地恢复出相位截断傅里叶变换加密系统原始图像的信息。这种新型的攻击是基于调制的振幅-相位迭代恢复算法，其中公钥RPM1和RPM2及密文是约束条件。它的收敛性是由迭代过程中的振幅K (x，y)和密文C (x，y)的均方误差(MSE)决定的，其中K (i，j)和C (i，j)分别表示图像对应像素点的像素值，[M，N ]表示图像矩阵的大小。当MSE的值或迭代次数达到预设的值时循环停止。MSE可表示为:

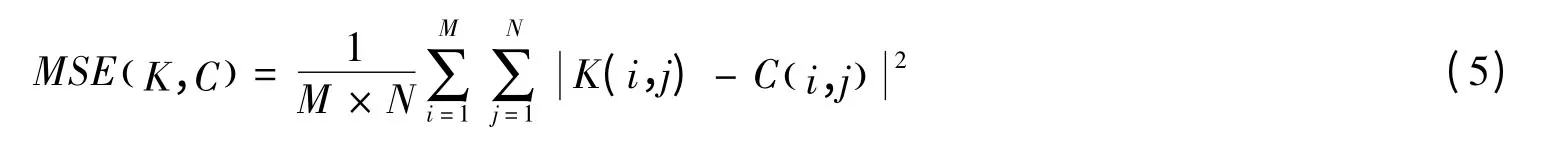
用这种新型的攻击算法去攻击经过改进后的相位截断傅里叶变换加密系统，攻击结果如图2所示，图2(a)为原始图像，图2(b)为k=0.5时的加密图像，图2(c)为对其攻击所得的结果，图2(d)为密钥全部正确时的解密结果。从中可以看出原始图像的信息被攻击。当k的取值变小时，是否都可以得到原始图像的信息呢?模拟结果如图3所示。图3(a)为k=0.2时的Lena 加密图像，图3(b)为攻击后的图像，此时无法观察到任何原始图像的任何信息了，迭代次数为250次时，MSE的值为0.003。图3(c)为循环30次时k的取值和MSE值的关系曲线图，从图3(c)中可以看出，k的取值越小，MSE的取值就越大，系统的安全性就越高;k的取值越接近于1，MSE的取值就越小，系统的安全性就越低。分析发现，当某一像素的周围像素值扩大或缩小超过10倍以上时，图像像素之间的关联性就得到了破坏，图像就很难被攻击出来了。

图2 模拟攻击结果

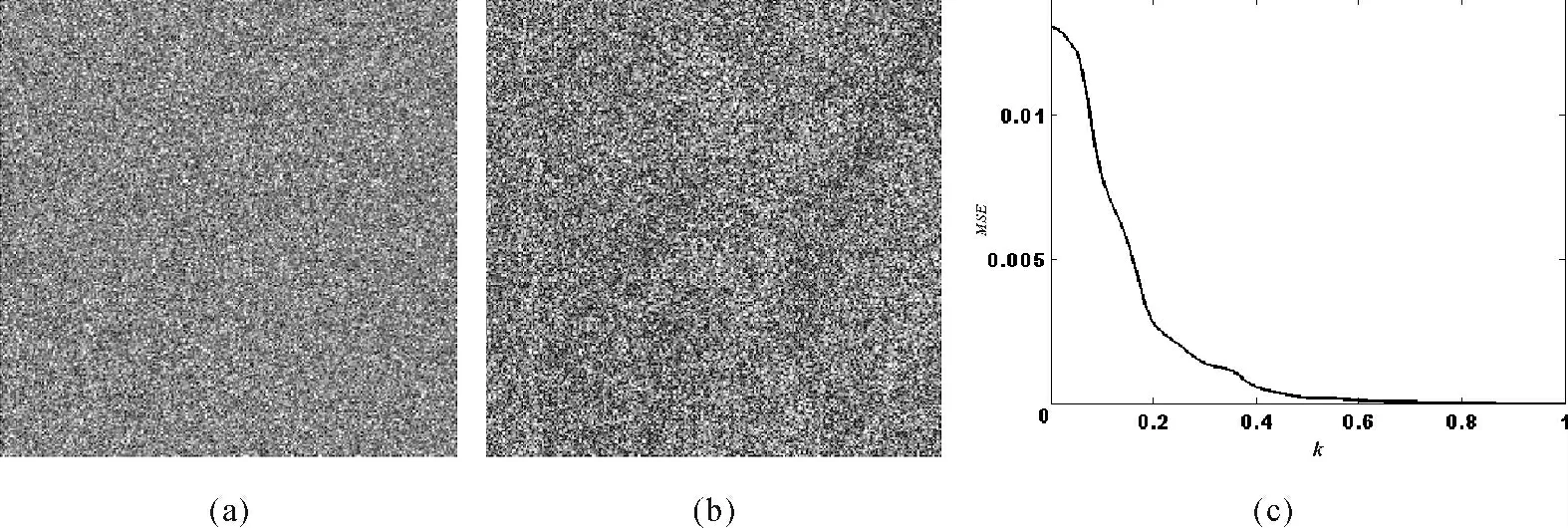
图3 不同k值的模拟结果

3 对随机振幅掩膜的改进

由前面的分析得知，当k的取值越小这种攻击就会变得更加困难，所以本文设计了一种特殊的振幅掩膜板，放置在相位截断傅里叶变换加密系统的傅里叶频谱面上。A1(u，v)的振幅透过率在 [0，1]上是均匀随机分布，设振幅透过率阈值为r，则:

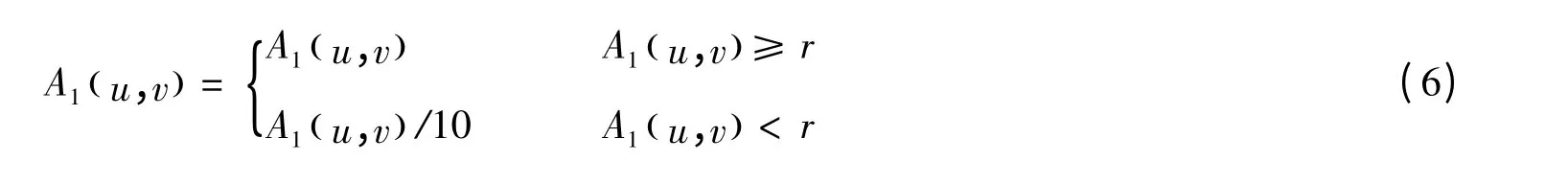
解密过程如下:

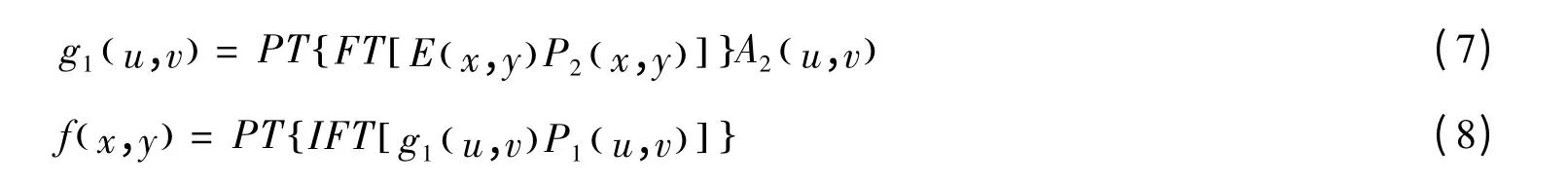
需要的指出是:A2(u，v)是A1(u，v)的倒数，即A1(u，v)·A2(u，v)=1。通过式(7)和式(8)得到原始图像，同时A2(u，v) 又可以作为一个附加的密钥。

4 计算机模拟结果及分析

对改进振幅掩膜板后的加密系统进行安全性分析，加密解密模拟结果如图4所示。图4(a)为原始图像，图4(b)为改进后的振幅掩膜，其中r=0.8，p=0.8，p表示振幅掩膜中像素值小于阈值r的像素在全部像素中所占的比例，图4(c)为加密后的图像，图4(d)为密钥全部正确的情况下恢复的图像。

图4 加密解密模拟结果

用新的攻击方法对该加密系统进行攻击，这里阈值r=0.7，p=0.7。结果如图5所示，图5(a)图5(c)为不同迭代次数所对应的攻击结果，分别为30次、150次和350次，图5中看不到任何与原始图像有关的信息。图5(d)为迭代次数和MSE值的关系曲线，可以看出，随着迭代次数的增加MSE的值趋向于平行而不减小，因此无法恢复出原始图像。所以经过改进后的相位截断傅里叶变换非对称加密系统可以抵抗这种新型的攻击，安全性有了进一步地提升。

图5 不同迭代次数的解密图像

5 结束语

通过对傅里叶频谱域振幅掩膜的改进，本文提出了一种新的基于截断傅里叶变换的非对称加密系统。公钥由两块随机相位板组成，在加密过程中产生两个相位私钥，频谱域的振幅掩膜也可以作为一个附加的密钥。在仅知道公钥和密文的情况下，各种常见的攻击方法都无法获得原始图像的任何信息。说明经过改进的加密系统的安全性有了很大地提升。在光学信息加密领域，非对称光学加密系统仍将是以后发展的一个重要方向。

[1]Pefregier P，Javidi B.Optical image encryption based on input plane and Fourier plane random encoding[J].Optics Letters，1995，20(7):767-769.

[2]Unnikrishan G，Joseph J，Singh K.Optical encryption by double-random phase encoding in the fractional Fourier domain[J].Optics Letters，2000，25(12):887-889.

[3]Situ G H，Zhang J J.Double random-phase encoding in the Fresnel domain[J].Optics Letters，2004，29(14):1584-1586.

[4]史稀诗，司徒国海，张静娟.级联菲涅尔衍射光学图像安全系统[J].光子学报，2008，37(9):1779-1782.

[5]Peng X，Wei H Z，Zhang P.Chosen-plaintext attack on lensless double-random phase encoding in the Fresnel domain[J].Optics Letters，2006，31(22):3261-3263.

[6]Peng X，Zhang P，Wei H Z，et al.Known-plaintext attack on optical encryption based on double random phase keys[J].Optics Letters，2006，31(8):1044-1046.

[7]Qin W，Peng X.Asymmetric cryptosystem based on phase-truncated Fourier transforms[J].Optics Letters，2010，35(2):118-120.

[8]Wang X G，Zhao D M.A special attack on the asymmetric cryptosystem based on phase-truncated Fourier transforms[J].Optics Communications，2012，285(6):1078-1081.

[9]Wang X G，Zhao D M.Amplitude-phase retrieval attack free cryptosystem based on direct attack to phase-truncated Fourier-transform-based encryption using a random amplitude mask[J].Optics Letters，2013，38(18):3684-3686.

[10]Wang X G，Zhao D M.Security enhancement of a phase-truncation based image encryption algorithm[J].Applied optics，2011，50(36):6645-6651.

[11]Wang X G，Zhao D M.Discussion and a new attack of the optical asymmetric cryptosystem based on phase-truncated Fourier transform[J].Applied optics，2014，53(2):208-213.