负m次幂函数与排列数的交错级数型线性微分方程

高忠社，孙小瑞

（天水师范学院 数学与统计学院，甘肃 天水 741001）

负m次幂函数与排列数的交错级数型线性微分方程

高忠社，孙小瑞

（天水师范学院 数学与统计学院，甘肃 天水 741001）

使用数学归纳法证明了把系数中含有负m次幂函数与排列数的交错级数型线性微分方程化为可逐次积分的线性微分方程结论,并给出了求解此类方程通解的方法，最后通过例子进行了说明.

负m次幂函数；排列数；交错项级数；通解

引言

微分方程

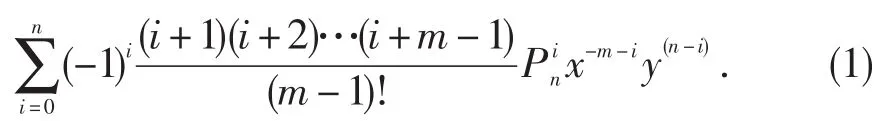
根据文献[2-6]对含负 j(j=1,2,3,4,5)次幂函数与排列数的交错级数型线性微分方程的解法探讨的启示,这类方程可用逐次积分的方法求解,故需将其化为可逐次积分的线性微分方程.文中给出了方程(1)通解的求法,以下是主要定理及其证明过程,并通过例题介绍其应用.

1　主要结果的证明及其应用

定理1

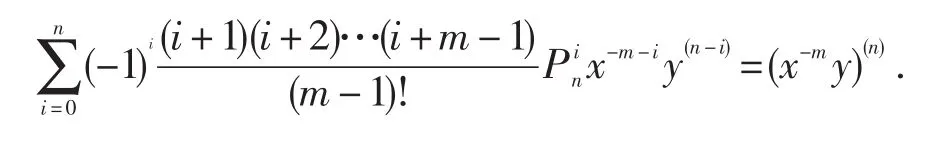
(3)下证当n=k+1时等式成立,对(2)式两边求导得

证得当n=k+1时(3)式等式成立.

综上所述，对任意自然数n等式成立,即

定理2微分方程

证明 由定理1可知微分方程

对(4)式两边积分得y=xm[∫[∫…[∫f(x)dx]…]dx]dx,故定理2成立.

例1求微分方程

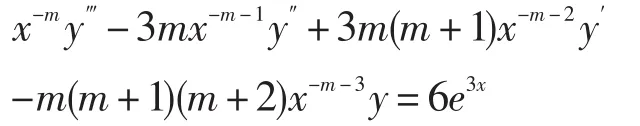
的通解.

解原方程为

推论2线性微分方程

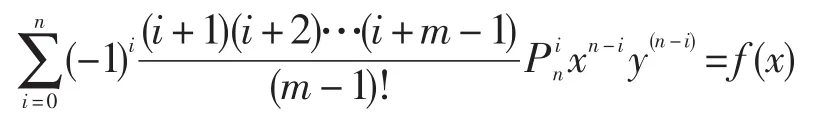
的通解为y=xm[∫[∫…[∫x-n-mf(x)dx]…]dx]dx,积分符号共有n个.

对(6)式两边逐次积分得

y=xm[∫[∫…[∫x-n-mf(x)dx]…]dx]dx,共有n个积分符号.

例2求线性微分方程

的通解.

解 原微分方程为

对(7)式两边逐次积分可得

故所求微分方程的通解为

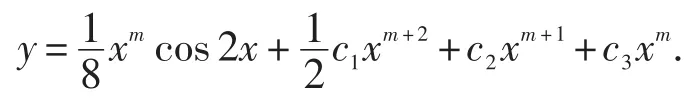
推论3线性齐次微分方程

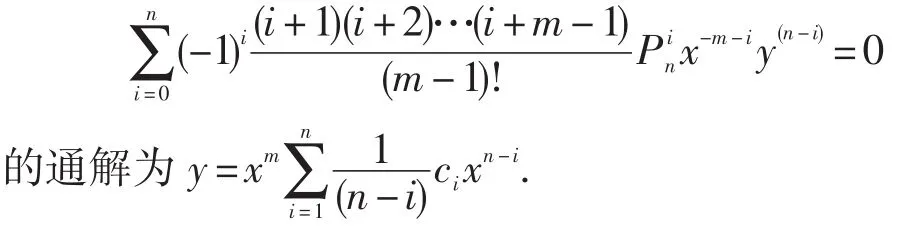
证明 线性齐次微分方程，即为(x-my)(n)=0,两边逐次积分可得

故所求通解为

例3求微分方程

x-my″-2mx-m-1y′+m(m+1)x-m-2y=0的通解.

解 原齐次微分方程可化为

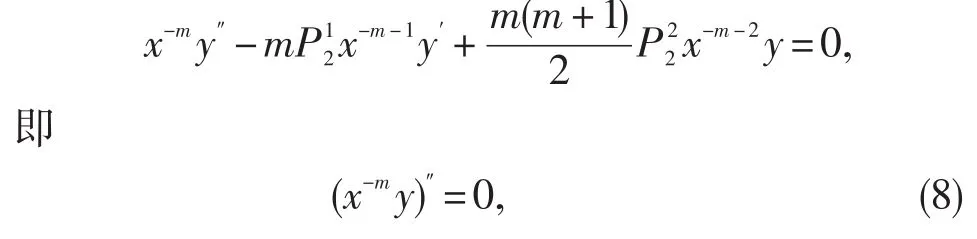
对(8)式两边逐次积分可得

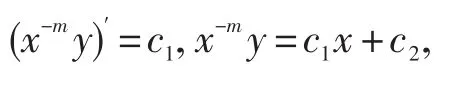
故所求通解为

2　总　结

文中主要介绍了系数含有负m次幂函数与排列数的交错级数型线性微分方程化为可以逐次积分的线性微分方程的方法，并用数学归纳法对其进行了证明.其次，给出这类方程通解的求解方法及其推论的证明过程，并分别加以例子说明其应用.最后给出求解此类齐次线性方程的通解的方法，且通过例子进行了说明.通过文中结论可知，求解此类问题时并不一定要严格按照给出的通解公式求解，可以由定理1将方程化为(x-my)(″)=f(x)，再对等式两边逐次积分即可求出方程的通解.

[1]王高雄,周之铭,朱思铭,王寿松.常微分方程[M].北京：高等教育出版社,2006.

[2]孙长军.一类可化为逐次积分的n阶线性微分方程的解法[J].河北理工学院学报,2004,26(3)：79-82.

[3]孙长军.负二次幂函数与排列数的交错级数型线性微分方程[J].山东理工大学学报,2004,18(5)：86-89.

[4]孙长军.负三次幂函数与排列数的交错级数型线性微分方程[J].河北理工学院学报,2005,27(3)：88-91.

[5]孙长军.负四次幂函数与排列数的交错级数型线性微分方程[J].成都大学学报,2006,25(1)：12-15.

[6]梁雪峰,郭振,田俊红.负五次幂函数与排列数的交错级数型线性微分方程[J].天水师范学院学报,2014,34(2)：11-12.

〔责任编辑艾小刚〕

Alternating Series Type of Linear Differential Equation of Negative m Numbers of Times of Power Function and Number of Permutation

Gao Zhongshe,SunXiaorui
(School of Mathematics and Statistics,Tianshui Normal University,Tianshui Gansu74100,China)

Mathematical induction is used to prove the conclusion that the alternating series type of linear differential equation of negative m numbers of times of power function and number of permutation is reduced to successive integral linear differential equation,and the general solution to this kind of equations is provided with examples following.

negative m numbers of times of power function;number of permutation;alternating series;general solution

O175

A

1671-1351（2015）05-0001-03

2015-06-26

高忠社（1979-），男，甘肃宁县人，天水师范学院数学与统计学院副教授，硕士。