堆芯熔融物对压力容器壁面烧蚀过程的数值模拟

张小英 姚婷婷 李志威 黄 凯

1（华南理工大学 电力学院 广州 510640）

2（中科华核电技术研究院 深圳 518026）

堆芯熔融物对压力容器壁面烧蚀过程的数值模拟

张小英1姚婷婷1李志威1黄 凯2

1（华南理工大学 电力学院 广州 510640）

2（中科华核电技术研究院 深圳 518026）

研究堆芯熔融物对压力容器壁面的动态烧蚀，对于反应堆冷却剂严重丧失事故(Loss of coolant accident, LOCA)后果的预测以及缓解方案的设计具有重要意义。本文以AP600为研究对象，在假设冷却剂全部丧失事故工况下，采用堆芯熔融物两层结构模型，计算熔池对壁面的加热；建立压力容器壁面的非稳态二维传热模型，并考虑安全壳水池对压力容器外侧的冷却，采用移动边界模型模拟烧蚀引起壁面局部厚度变薄；计算了堆芯熔融物坍塌后15000s范围内，压力容器下封头壁面温度和厚度的变化。

反应堆，冷却剂丧失，堆芯熔融物，压力容器，壁面烧蚀

在反应堆发生冷却剂严重丧失事故(Loss of coolant accident, LOCA)[1]后，堆芯由于长时间得不到冷却而发生熔化，堆芯熔融物跌落到压力容器底部，使底部结构受到持续强烈的加热而烧蚀，破坏压力容器底部结构的完整性。因此，研究堆芯熔融物对压力容器下封头材料的烧蚀问题，对于预测反应堆冷却剂严重丧失事故的发生以及研究相应的缓解方案都有重要的参考意义。对此， 采用熔池分层结构研究了下封头壁面的热负荷[2]，并假定材料厚度不变情况下，采用二维导热模型计算壁面温度；基于熔池两层结构模型，计算了对下封头壁面的对流与辐射热流[3]，用一体化严重事故计算程序计算了小破口和大破口事故下，下封头壁面的热流密度和熔池结构[4]。

炽热的堆芯熔融物沉积在压力容器下封头，强烈加热壁面材料，引起壁面局部烧蚀，危及压力容器的完整性。对于堆芯熔融物加热作用下，压力容器壁面的温度上升及烧蚀过程还有待研究。为此，本文建立了熔池下封头壁面传热模型，其中熔池采用两层结构模型，壁面传热采用非稳态二维传热模型，熔池对壁面加热考虑对流和辐射换热，非稳态计算中壁面烧蚀引起局部厚度的变化采用移动边界模型。在假设压力容器沉浸于安全壳水池中，外壁温度接近安全壳环境压力下的饱和水温度情况下，计算了AP600反应堆[5–7]堆芯熔融物坍塌后15000s范围内，壁面温度及厚度的变化。

1 熔池两层结构模型

反应堆堆芯熔融后，形成铀氧化物和金属熔融物，由于铀氧化物密度大，其熔融物沉积在熔池的下部，金属熔融物的密度较轻，浮升在熔池的上部，故采用图1所示的两层结构模型[8]，模拟堆芯熔融物在压力容器下封头的滞留状态。铀氧化物熔池周边由于与温度较低的压力容器壁面和金属熔融层接触，形成薄薄一层凝固壳层(图2)。根据堆芯熔融物的体积，由于下封头形状近似为球形，从球冠的体积可依据式(1)计算熔融层高度，得到铀氧化物熔池的高度HU和金属熔融层的高度HM，及铀氧化物熔池和金属熔融层上表面的极角Uθ和Mθ。

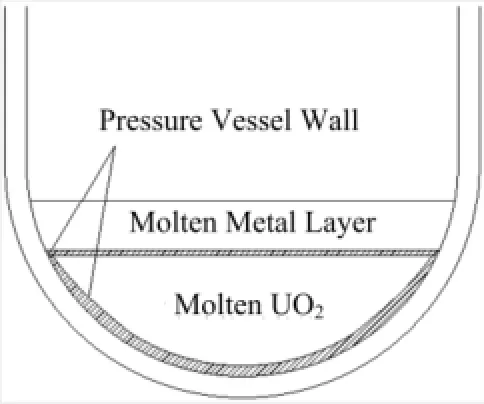
图1 堆芯熔融物在压力容器下封头形成的两层结构熔池Fig.1 Two-layer structure of melt core in the lower head of pressure vessel.

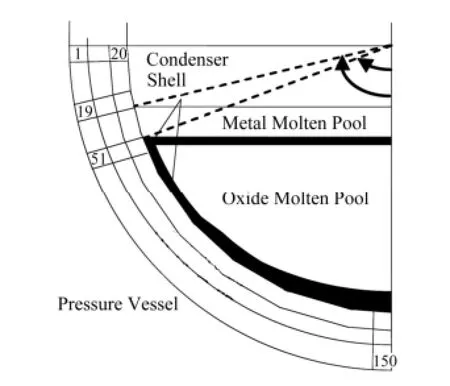
图2 壁面网格离散化示意图Fig.2 Grid discretization of the pressure vessel wall.

2 压力容器壁面传热的计算模型

2.1 微分方程及离散

为计算堆芯熔融物对压力容器壁面的烧蚀过程，考虑到压力容器下封头的球面形状，几何上具有轴对称性，因此对压力容器下封头壁面的传热可采用沿壁面厚度和下封头圆周角的二维球面导热模型，见图3所示，AB段为熔池以上的部分，BC段为金属熔池部分，CD段为铀氧化物熔池部分。壁面导热的微分方程为：

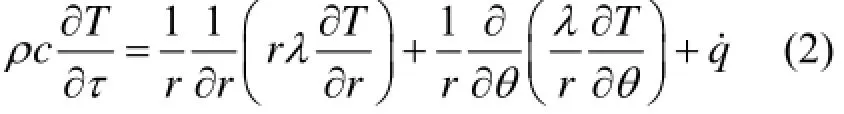
对图3所示的下封头壁面沿半径和圆周角方向等间隔划分控制体，采用控制容积积分法得到离散方程为[9]：

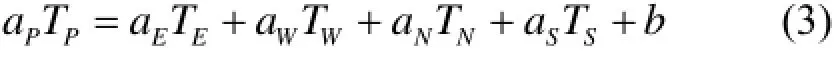
其中：

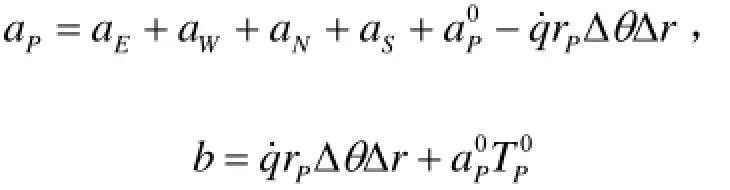
在熔池对压力容器壁面的烧蚀过程中，压力容器壁面局部因烧蚀而变薄，故壁面传热的计算区域将发生变化[10]。为模拟壁面烧蚀过程中计算区域的变化，本文采用移动边界模型。对每一个新的计算时刻，首先判断前一时刻的壁面温度，将超过材料熔点的那些节点从计算域中去掉，采用未熔的节点构造新的计算域，如图4所示。

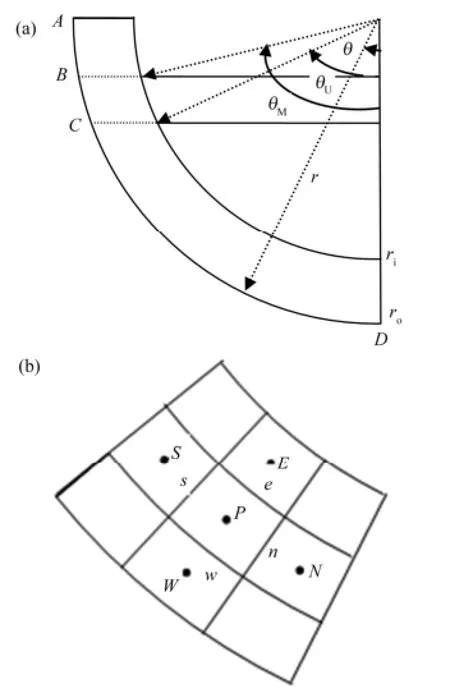
图3 压力容器壁面传热计算几何模型 (a) 径向，(b) 局部Fig.3 Geometry model of heat analysis of pressure vessel wall. (a) Radial, (b) Part

图4 移动边界模型示意图Fig.4 Moving boundary model scheme.

2.2 计算的边界条件

对于边界控制体的离散方程，采用补充虚拟边界控制体方法，并令虚拟边界控制体的温度始终等于相邻边界控制体的温度，由此边界控制体与虚拟控制体之间虽有导热项却没有导热热流，式(3)对边界控制体可适用。在壁面内侧，需计算壁面与熔池的对流与辐射换热。壁面外侧浸泡在安全壳水池中，近壁区的水受到壁面加热达到沸腾，因此可令外壁温度接近安全壳压力下水的饱和温度。

图3所示的压力容器内侧边界各部分的受热不同，需分别计算。AB段的内边界热流需计算金属熔池上表面对壁面的辐射换热；BC段的内边界热流需计算金属熔池对壁面的对流换热凝固壳层的释热；CD段的内边界热流需计算铀氧化物熔池对壁面的对流换热。

为计算AB段内边界的辐射热流qW,r，只考虑金属熔融层上表面对壁面的辐射，忽略压力容器的自辐射反射，根据Lambert定律计算金属熔融层对压力容器内表面的净辐射热流：

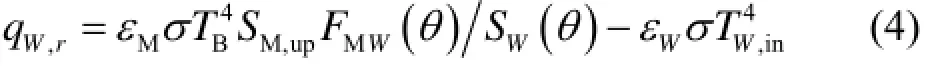
BC段内边界的热流为金属熔融层对壁面的对流热流MWq，计算为：

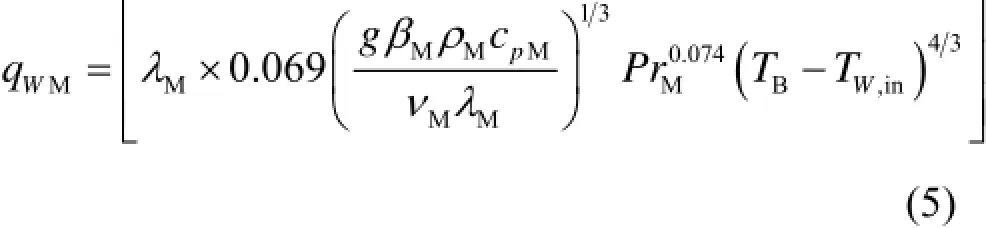
式中，BT是金属熔融层主体温度，K，需根据金属熔融层的换热计算。

CD段内边界的热流包括铀氧化物熔池对壁面的对流换热qU,dn(θ)及凝固壳层的释热：

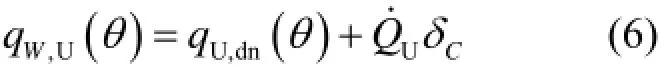
根据文献[2]，铀氧化物熔池由于温度分层形成上对流层和下对流层，上对流层与金属熔融层对流换热，下对流层与壁面对流换热，换热热流计算为：式中，U,dnq为下对流层与所接触壁面的平均换热热流。

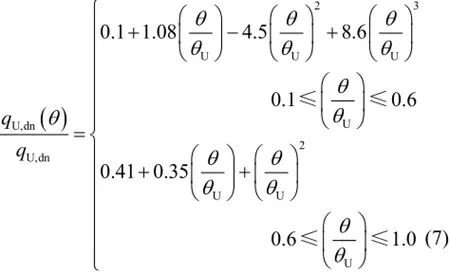
式中，'Ra是内部Rayleigh数。

2.3 金属熔融层主体温度TB的计算

在前面计算金属熔池对压力容器内壁的对流与辐射换热当中，均用到金属熔池的主体温度TB。为计算TB，对金属熔融层列热平衡方程，单位时间铀氧化物熔池通过对流传给上凝固壳层，并进一步传给金属熔池的热量MUq，等于金属熔池向压力容器壁面的辐射换热量,Wrq和对流换热量MWq之和，即：

式中，AM是熔池的横截面积；AW是与金属熔池接触的压力容器内壁面积；FM–W是金属熔池对压力容器AB段内壁的辐射角系数。铀氧化物熔池对金属熔融层的对流换热计算采用Globe Dropkin的关系式计算[11]：

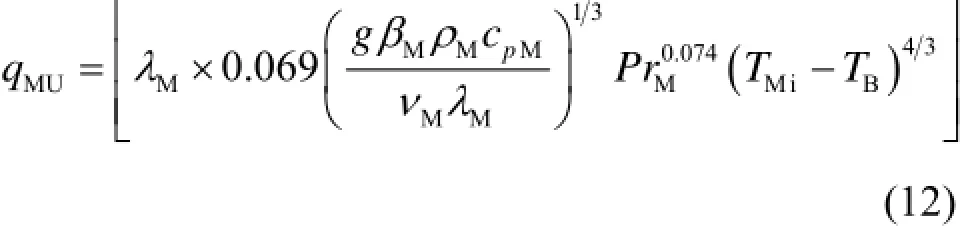
将式(5)、(6)、(12)代入式(11)，TW,in采用前一计算时刻的数值，求解可得到金属熔池的主体温度TB。

2.4 凝固壳层厚度的计算

凝固壳层厚度是熔池结构的重要参数，为计算凝固壳层的厚度，采用一维平板导热模型，对凝固壳层和压力容器壁面沿厚度方向列热平衡方程，即凝固壳层的径向导热热流=压力容器的径向导热热流=熔池对壁面的对流热流+堆芯的衰变热流，由此求解得到凝固壳层的厚度。

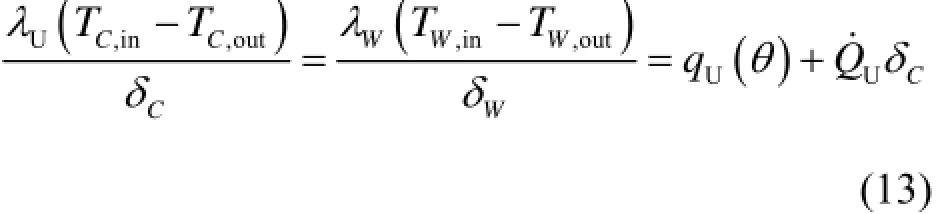
3 计算结果与分析

在计算压力容器下封头壁面温度时，取计算段高度为下封头至金属熔融层以上0.5m高度的壁面，考虑几何的对称性，取一个圆周方向的壁面加以计算，有关参数如下：铀氧化物密度ρU=8450kg·m−3；铀氧化物熔点TU=2973K；铀氧化物热导率λU=5.3W·(m·K)−1；铀氧化物体积膨胀系数βU=1.05×10−4K−1；铀氧化物动力粘性系数铀氧化物发射率εU=0.8；AP600下封头半径R=2m；铀氧化物熔池体积VU=8.6 m3；金属熔池体积VM=3.14m3；金属熔融物密度ρM=6890kg·m−3；金属熔融物熔点TM=1600K；金属熔融物热导率λM=25.5W·(m·K)−1；金属熔融物体积膨胀系数βM=1.1×10−4K−1；金属熔融物动力粘性系数金属熔融物发射率εM=0.45；AP600压力容器壁厚δV=0.015m；AP600停堆4 h后，单位体积释热量压力容器壁面初始温度322K；安全壳工作压力0.1MPa。

本文计算堆芯熔融物对下封头壁面内侧的加热热流如图5(a)所示，相应地文献[2]计算的结果如图5(b)所示，文献给出了将金属熔融层以上壁面视为绝热（实线）和考虑金属熔融层以上壁面传热的两组结果（虚线）。可以看到：(1) 在下封头与铀氧化物熔池接触的部分，熔池对壁面的加热热流随倾角而上升；(2) 在下封头与金属熔融层接触的部分，加热热流下降，因为在金属熔融物以上部分的壁面主要的加热来自金属熔融层表面的辐射，热流比金属熔融层以下壁面受到的对流加热小得多，导致金属熔融层接触部分的壁面加热热流也有所下降。

本文计算铀氧化物熔池凝固壳层的厚度如图6(a)所示，而文献[2]根据严重事故下堆芯熔融物在压力容器内滞留的分析程序IVRASA计算得出的数据，以及USCB (DOE/ID-10460)和INEEL的实验数据如图6(b)所示。可以看到：(1) 凝固壳层厚度在压力容器下封头底部（倾角为零）最大，约为0.06m，随着倾角增大，壳层厚度逐渐减小，壳层顶部厚度约为 0.002m；(2) 本文计算的凝固壳层厚度数值及随倾角的变化规律与USCB (DOE/ID-10460)的实验结果一致性较好。

图5 封头壁面内侧的加热热流(a) 本文计算，(b) 文献[2]计算Fig.5 Heat flux at internal wall of downward part. (a) Our computation, (b) Ref.[2]

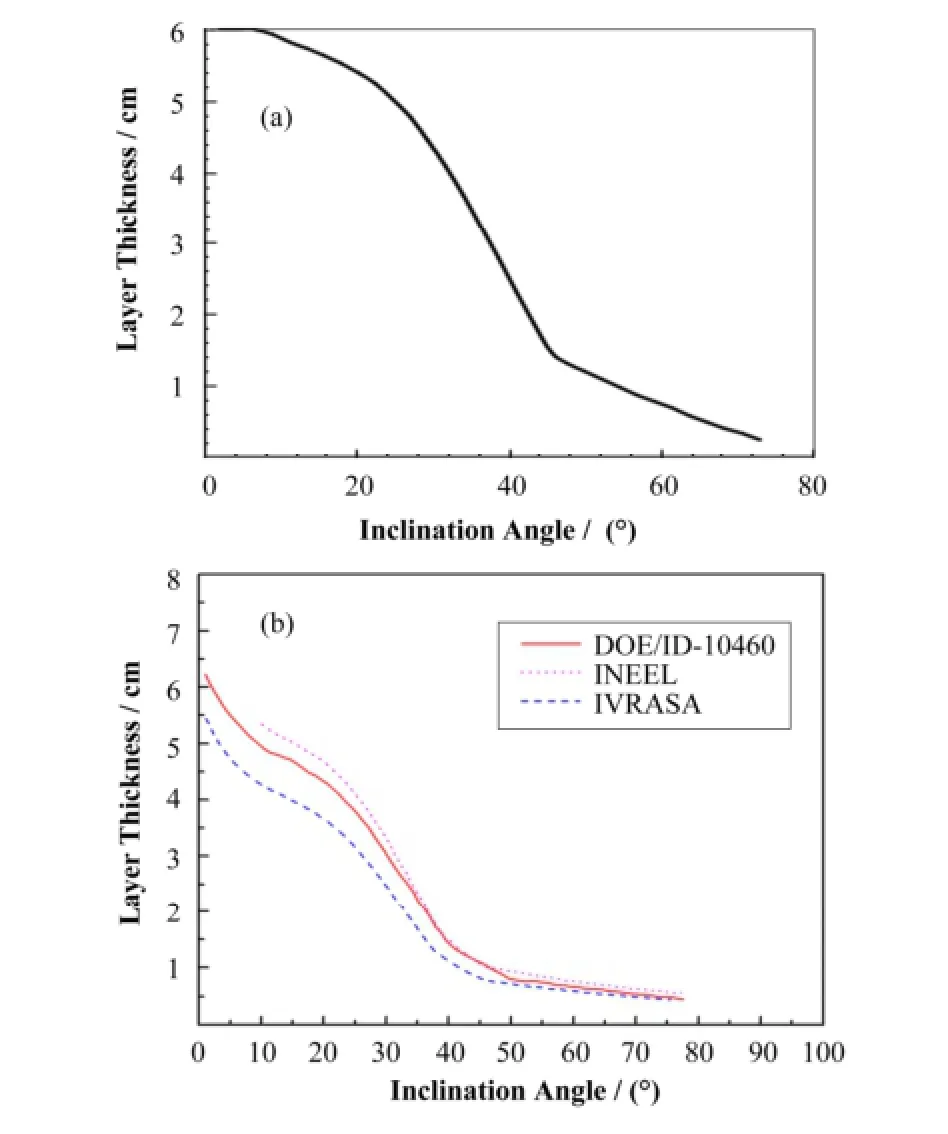
图6 铀氧化物熔池凝固壳层的厚度(a)，文献[2]凝固壳层的计算与实验数据(b)Fig.6 Thickness of condensed layer of UO2 (a), computing and experimental result of condensed layer in Ref.[2] (b).

本文计算在堆芯熔融物加热作用下，压力容器下封头壁面温度随时间的发展过程如图7所示，图7中共给出了自初始时刻至其后15000s范围内的计算结果。可以看到：(1) 从初始时刻开始，壁面温度逐渐上升，在1000s时金属熔池周围的壁面温度达到1500K，文献[2]中的图也表明，烧蚀点附近的壁面温度为1500K左右；(2) 当金属熔池周围的壁面温度超过压力容器壁面的熔点温度，如在2000s时，壁面发生烧蚀；(3) 熔池的热量不断向壁面深处传递，壁面温度全面上升，在3 000s及以后直至9000s的时间内，壁面上的烧蚀区域不断扩宽并加深；(4) 9000s以后，压力容器与熔池、外侧安全壳水池之间趋于热平衡，壁面温度分布与烧蚀区域形状与大小趋于稳定，如10000s和15000s的结果所示，与图8所示文献[2]中ABAQUS计算的壁面烧蚀轮廓相符。

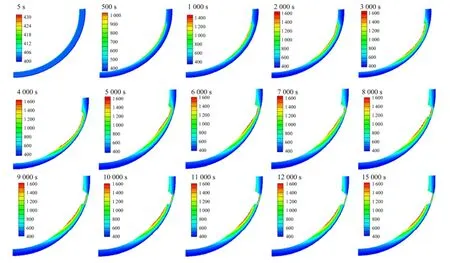
图7 压力容器下封头壁面厚度的变化Fig.7 Variation of wall thickness in downward part of pressure vessel.

图8 文献[2]中ABAQUS计算的壁面轮廓Fig.8 Wall configuration of wall in Ref.[2].

4 结语

采用堆芯熔融物的两层结构模型，计算熔池对压力容器下封头壁面的加热热流；建立壁面的移动边界二维平板导热模型，计算在熔池加热和安全壳水池冷却作用下，压力容器壁面的动态烧蚀过程；以AP600为研究对象，计算堆芯熔池形成后15000s范围内，压力容器下封头壁面温度及厚度的变化。

研究表明：(1) 铀氧化物熔池对下封头壁面的加热热流随倾角而上升，金属熔融层对壁面的加热热流略低；(2) 内壁温度随时间上升很快，两熔融层界面处最先出现烧蚀，之后烧蚀深度和宽度增加；(3) 在9000s以后，熔池-壁面-安全壳水池间趋于热平衡，壁面温度分布和烧蚀区基本不再发生变化。

1 Frepoli C. An overview of westinghouse realistic large break LOCA evaluation model[J]. Science and Technology of Nuclear Installations, 2008, 498737

2 Theofanous T G, Liu C. In-vessel coolability and retention of a core melt[J]. Nuclear Engineering and Design, 1997, 169: 1–48

3 Guan Z H, Yu H X, Jiang G M. Study on cooling model for debris in lower plenum and countermeasures for prevention of focusing effect[J]. Nuclear Engineering and Design, 2008, 29(5): 72–76

4 Fu X L, Yang Y H, Zhou W H, et al. Analysis of process for core melt and debris pool formation in IVR evaluation for CPR1000[J]. Nuclear Engineering and Design, 2010, 31(5): 102–107

5 Luis E H, Mark H A. A diffusion layer model for steam condensation within the AP600 containment[J]. Nuclear Engineering and Design, 1998, 183: 133–150

6 Rafael M J, Kostadin I. Numerical diffusion and the tracking of solute fields in system codes (Part III): application to a boron dilution transient analysis in the AP600[J]. Nuclear Engineering and Design, 1998, 179: 345–356

7 Mark H A, Luis E H. Experimental analysis of heat transfer within the AP600 containment under postulated accident conditions[J]. Nuclear Engineering and Design, 1998, 185: 153–172

8 Li L, Zang X N. The research on molten corium coolability measures for the PWR severe accident[J]. Nuclear Security, 2007, 4: 39–44

9 赵静, 余红星, 李锋. 1000MW级压水堆安全壳压力温度计算分析[J]. 核动力工程, 2003, 24(5): 409–411

ZHAO Jing, YU Hongxing, LI Feng. Calculation and analyses of containment pressure and temperature for PWR 1000MW[J]. Nuclear Engineering and Design, 2003, 24(5): 409–411

10 陶文铨. 数值传热学[M]. 第二版. 西安: 西安交通大学出版社, 2001 TAO Wenquan. Numerical heat transfer[M]. 2ndEd. Xi'an: Xi'an Jiao tong University Press, 2001

11 Globe S, Dropkin D. Natural-convection heat transfer in liquids confined by two horizontal plates and heated from below[J]. Journal of Heat Transfer, 1959, 81: 24–28

CLC TL99

Numerical simulation of the ablation process of the nuclear pressure vessel heated by core melt

ZHANG Xiaoying1YAO Tingting1LI Zhiwei1HUANG Kai2
1(School of Electricity, South China University of Technology, Guangzhou 510640, China) 2(China Nuclear Power Technology Research Institute, Shenzhen 518026, China)

Background: The study on the transient ablation of the pressure vessel wall, acted by the detained melt core, is very important for damage prediction after occurrence of serious loss of coolant accident (LOCA), and design of accident mitigation scheme. Purpose: This paper attempts to study the ablation process of downward part of pressure vessel of AP600, in condition of losing all coolant. Methods: A two-layer of melt material model was used to simulate the structure of melt core, and the heat flux on the vessel wall was computed. The unsteady 2-D heat conduction model was developed for the downward part of pressure vessel, and water boiling in containment was considered as cooling of outer wall. A moving boundary model was used to simulate the decreasing wall thickness on some point in the ablation process. The variation of wall temperature and thickness with time, from occurrence of the accident, till 3000s after the accident, was computed in detail. Results and Conclusion: Simulation results shows that heat flux from the molten UO2on the vessel wall grows up with increasing inclination angle, and heat flux from the molten metal is a little small. Temperature on internal wall grows up rapidly with time, which causes the ablation firstly appearing at interface of the two molten layers, and the ablation zone tends to deepen and widen after that. The heat balance between molten material, vessel wall and containment pool will come 9000s after occurrence of accident, and temperature and ablation zone would not change after 9000s.

Reactor, Coolant loss, Core melt, Pressure vessel, Wall ablation

TL99

10.11889/j.0253-3219.2015.hjs.38.020606

项目(No.51176052、No.51376065)资助

张小英，女，1973年出生，2002年于北京航空航天大学获博士学位，研究领域为反应堆热工水力计算、核电安全理论与技术

黄凯，E-mail: hkai@cgnpc.com.cn

2014-01-12，

2014-05-26