纳米器件的非零点能Casim ir排斥力
2015-11-30宋开宏王娟娟黄志祥吴先良
方 明,宋开宏,王娟娟,黄志祥,吴先良,2
(1.安徽大学计算智能与信号处理教育部重点实验室,合肥 230039;2.合肥师范学院物理与电子工程系,合肥 230061)
文章编号:1001⁃246X(2015)01⁃0101⁃06
纳米器件的非零点能Casim ir排斥力
方 明1,宋开宏1,王娟娟1,黄志祥1,吴先良1,2
(1.安徽大学计算智能与信号处理教育部重点实验室,合肥 230039;2.合肥师范学院物理与电子工程系,合肥 230061)
结合边界元方法,利用离散点表面电流及表面磁流的格林函数得到任意三维几何体及任意材料纳米器件互相作用离散点之间的Casimir力.给出浸泡在液体中纳米器件的“非零点能”Casimir效应,分析Casimir排斥力产生的条件,为实际纳米器件之间Casimir效应分析提供新的数值方法.
Casimir力;频域电磁算法;非零点能;Casimir排斥力
0 引言
Casimir效应是由荷兰物理学家Hendrik Casimir提出的,他指出真空中充满了各种波长的粒子,当两个不带电的金属板平行靠近时,会形成谐振腔较长波长粒子会被隔断在平板之外,导致平板系统外能量高于系统内产生吸引力,这就是Casimir效应[1].近十年随着微机电系统技术的发展,纳米器件之间Casimir效应越来越受到关注.如果纳米器件距离小于一定量级,器件之间的Casimir力将占主导地位成为强吸引力[2],它会使本来可以移动的器件粘滞在一起,导致微机电系统[3](MEMS)失效.所以需要一种精准的方法对复杂几何体微系统进行建模分析计算纳米器件之间的Casimir效应,尤其是Casimir排斥力[4],这是MEMS技术商用化的关键.
近年来国内外很多学者做了很多Casimir排斥力的研究,给出了几种Casimir排斥力产生的方法,如使用特殊材料:左手材料[5]、负折射材料[6]、各向异性单负超材料[7]、基于饱和亚硝酸盐对Casimir力极性调节[8]和通过磁光效应理论[9]等,以及特殊的系统中:浸没在液体中的介质体之间[10],交错间隔的几何体之间[11].但是都只给出了Casimir排斥力产生的条件,或者简单理想模型Casimir力的计算.真实MEMS应用中需要面对任意温度下复杂的三维几何体任意材料的器件Casimir力,所以分析Casimir排斥力产生条件需要精确的数值方法.本文使用频域电磁算法边界元法,通过经典电磁理论频域求解散射问题,通过电磁场的量子化得到物体表面的Maxwell应力张量,由应力张量得到Casimir力.计算出MEMS中器件之间Casimir排斥力产生的距离范围,甚至得到吸引力转变为排斥力的平衡位置,克服MEMS器件粘附现象.
1 基本原理
1.1 基于Maxwell应力张量求解Casimir效应
通常计算Casimir效应从两方面出发,①是直接计算各模式真空零点能进行重正化[12],该方法对于对称几何体之间Casimir计算可以快速收敛而且精度较高,但是此方法只适合简单的模型,对复杂几何体很难操作;②是使用Maxwell应力张量[13].本文使用应力张量方法,结合电磁算法可以求解任意材料和几何体之间Casimir力.
如图1所示,考虑两个任意材料的三维物体A和B放置在真空中,根据“零点能”理论,真空环境中存在无穷多频点的电磁能,A和B会改变真空中“零点能”的边界.B表面S面上会产生感应电流,这些感应电流产生的散射电磁场会在A上产生的Maxwell应力张量,对A表面S′应力张量面积分即为A和B之间的Casimir力
FCasimir= ∮S′
Fm=∫∞
0
∮S′
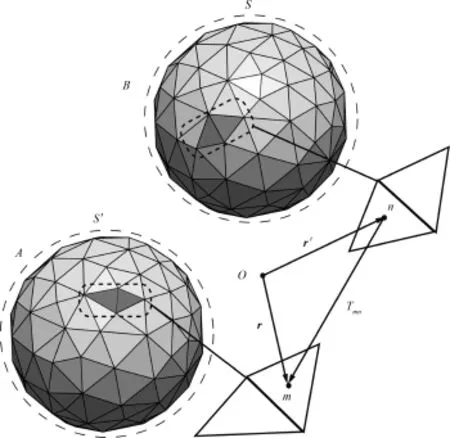
图1 两个物体使用三角形面元离散,使用RWG基函数对电磁流描述Fig.1 Schematic of electromagnetic currents discreted by RWG basis functions

Fm(ξ)dξ. (1) Fm(ξ)表示A上的m点在虚频率ξ下Casimir力频点分量,它可以表示为对物体B表面S的面积分(r)表示S面上r点的内法线方向,Tmn表示n点电磁流对应的散射电磁场在m点产生的Maxwell应力张量,对电磁场进行量子化可以得到
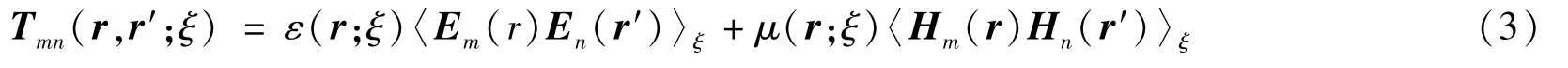
在绝对零度,将上式中〈Em(r)En(r′)ξ〉和〈Hm(r)Hn(r′)ξ记为
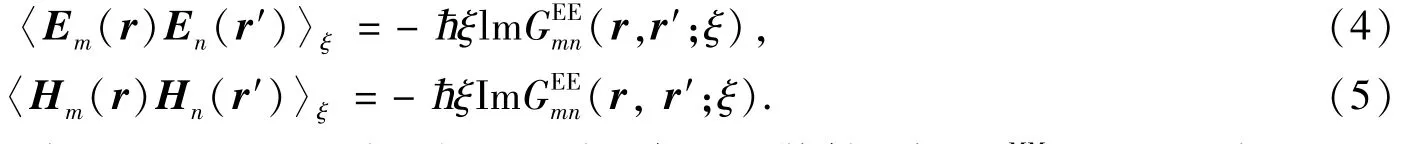
ħ为普朗克常量,GEEmn(r,r′;ξ)表示电流源r′(n点)在r(m点)产生的散射电场,GMMmn(r,r′;ξ)表示磁流源r′(n点)在r(m点)产生的散射磁场.将(2)-(4)式代入(1)便可以得到m点Casimir力的为
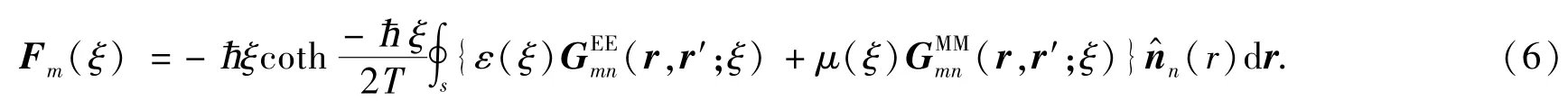
所以对于任意材料和几何体物体之间的Casimir力计算首先我们要得到GEEmn(r,r′;ξ)和GMMmn(r,r′;ξ)两个格林函数.
1.2 离散求解
对经典电磁理论部分求解使用PMCHW方程[14],分别由等效原理和介质体表面电磁场切向连续边界条件可以得到介质体内外的电场积分方程和磁场积分方程,将电场积分方程和磁场积分方程叠加可得到PMCHW方程
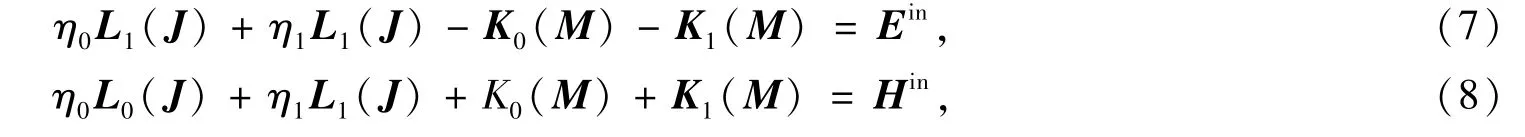
这里L0、L1、K0和K1为积分算子[14],对电流和磁流使用RWG基函数[15]离散J(r)=∑ajafa(r),M(r)=∑amafa(r).使用加勒金法进行检测可得到矩阵方程

通过求解矩阵方程(9)得到电流和磁流离散系数,通过该系数可以得到散射场.记PMCHW阻抗矩阵的逆为

则待求电流磁流为

将RHS向量中的激励场更换为n点上的点电磁流源在m点产生的电磁场,计算m点电磁流产生的散射场即可得到(r,r′;ξ)和(r,r′;ξ),由此可得到
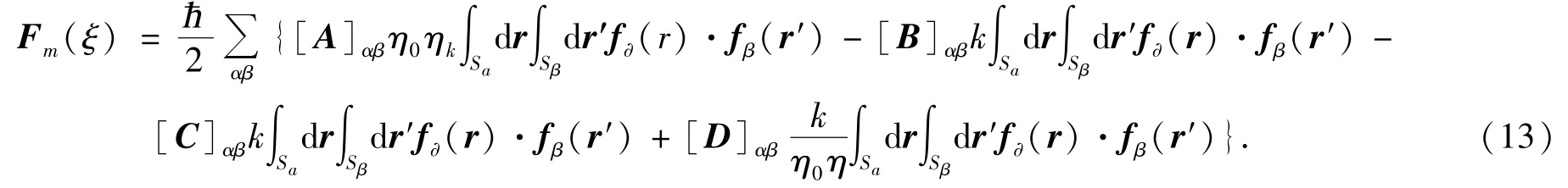
将(13)式代入到(1)式中,得到物体间相互作用Casimir力为
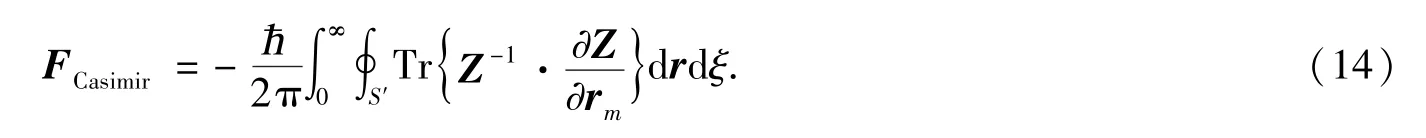
2 计算结果
2.1 Casimir排斥力分析

图2 各种材料相对介电常数ε(iξ)随虚频率ξ变化Fig.2 Materials relative permitivity as functions of image frequency
如图2所示,使用Drude⁃Lorentz模型描述不同色散材料虚频率下相对介电常数随频率的变化.浸没在液体里介质体之间的介电常数满足
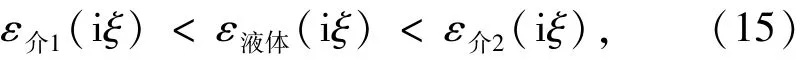
则此时Casimir力表现为排斥力[16],即在液体的虚频率相对介电常数介于两介质之间时,介质体之间Casimir力为排斥力.当两个物体距离较近时,高频率Casimir分量占到主导地位;而在物体距离较远时,低频率Casimir分量占主导地位[17].由此可以推测两个材料为聚四氟乙烯和硅的器件放入乙醇中,当两物体距离较近时Casimir力为排斥力而距离较远时为吸引力.为了验证这个猜想使用本文方法计算不同材料放在液体中的Casimir力,同时准确地计算出物体之间的平衡距离(物体之间Casimir力为0).
如图3所示,两个浸没在乙醇液体中平行放置的立方体边长分别为150 nm和300 nm,计算不同材料下两个立方体之间的Casimir力(曲线上方标注前者为小立方体材料后者为大立方体材料),曲线都是使用PFA Casimir力归一化[18].本文归一化方式是首先计算出介质体之间Casimir力,然后使用介质体相同的几何模型,将介质体的介电参数改为理想导体,计算出此时的Casimir力,使用后者的Casimir力对介质体计算结果进行归一化.图中归一化Casimir力为正表示吸引力,负值表示排斥力.计算结果与预测趋势相同,同时给出了不同材料之间的平衡距离.
2.2 非零点能Casimir力计算
对于非零点能Casimir计算,需要在式(3)量子化过程加入温度T的影响[18].则(4)、(5)式改写为
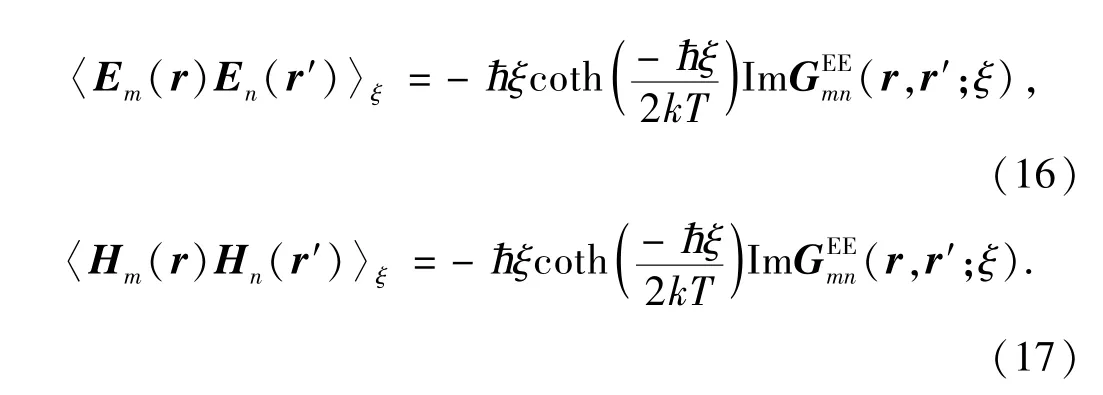
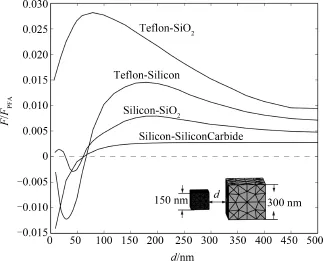
图3 不同材料立方体之间经PFA归一化的Casimir力随距离变化Fig.3 Casimir force between cubes with differentmaterials normalized with PFA predictions
如图4(a)所示模型,高为50 nm,直径为120 nm的聚四氟乙烯圆饼和厚度为100 nm长度为400 nm的正方形硅板浸没在乙醇中.图4(b)所示曲线,为圆饼旋转角度为0°时,在不同温度下,Casimir力随着聚四氟乙烯圆饼和正方形硅板距离变化.图中可以看出温度对Casimir力的影响,随着温度从0 K增加到400 K,Casimir力平衡距离从58 nm逐渐增加到100 nm.将聚四氟乙烯圆饼旋转,图4(c)所示曲线,计算圆饼旋转不同角度下Z方向的Casimir力,随着旋转角度增大,圆饼在硅板上的投影变小,Casimir平衡距离逐渐变大.
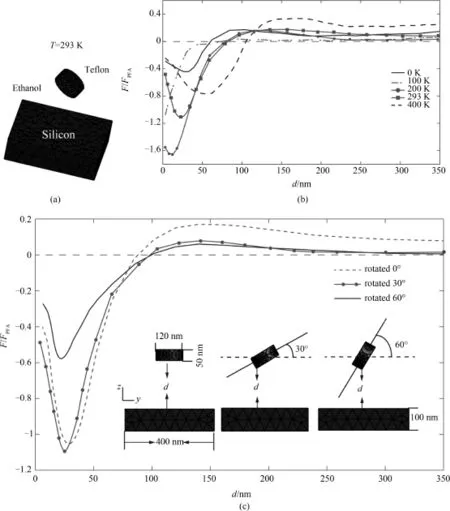
图4 常温下聚四氟乙烯圆柱和硅板浸没在乙醇中不同放置下Casimir力Fig.4 Casimir forces between silicon plate and Teflon cylinder immersed in ethanol
3 结论
使用频域电磁方法即边界元法对经典量子现象Casimir效应求解,对Drude⁃Lorentz模型的色散材料任意几何体器件表面电磁流使用RWG基函数进行离散,求解经典电磁场理论中的散射问题,经过电磁场量子化得到离散元上的Maxwell应力张量.由应力张量得到Casimir力.本文给出的几个算例包括不同材料物体之间Casimir力计算,分析了Casimir力排斥力出现的条件并且通过计算得到验证.同时从实际应用出发,给出非零点能Casimir力计算方法,为实际应用MEMS系统器件之间Casimir效应分析提供了精确的数值方法.
[1] Casimir H B G.On the attraction between two perfectly conducting plates[J].Proc Kon,1948,51:793.
[2] Buks E,Roukes M L.Stiction adhesion energy and the Casimir effect in micromechanical systems[J].Physical Review B,2011,63:033402.
[3] 樊康旗,贾建援,朱应敏,刘小院.原子力显微镜在轻巧模式下的动力学模型[J].物理学报,2007,56:6345-6351.
[4] Buks E,Roukes M L.Stiction adhesion energy and the Casimir effect in micromechanical systems[J].Physical Review B,2001,63:033402.
[5] Yang Y,Zeng R,Xu JP,Liu S T.Casimir force between left⁃handed⁃material slabs[J].Physical Review A,2008,77:015803.
[6] 曾然,羊亚平,刘树田.负折射率材料对产生Casimir排斥力的影响[J].物理学报,2008,57:4947-4952.
[7] Zeng R,Yang Y P,Zhu SY.Casimir force between anisotropic single⁃negativemetamaterials[J].Physical Review A,2013,87:063823.
[8] Zeng R,Yang Y P.Tunable polarity of the Casimir force based on saturated ferrites[J].Physical Review A,2011,83:012517.
[9] Zeng R,Yang Y P.Repulsive and restoring casimir forces based onmagneto⁃optical effect[J].Chinese Physical Letter,2011,28:054201.
[10] Munday J,Capasso F,Parsegia V A.Measured long⁃range repulsive Casimir⁃Lifshitz forces[J].Nature,2008,457:170.
[11] Rodriguez AW,Joannopoulos JD,Johnson SG.Repulsive and attractive Casimir forces in a glide symmetric geometry[J]. Physical Review A.2008,77:062107.
[12] Klinchitskaya G L,Mohideen U,Mostepanenko V M.Casimir and van derWaals forces between two plates or a sphere(lens)above a platemade of realmetals[J].Physical Review A.2000,61:062107.
[13] TomašM S.Opposites attract:A theorem about the Casimir force[J].Physical Review Letter.1995,97:160401.
[14] Medgyesi⁃Mitschang L N,Putnam J M,Gedera M B.Generalized method of moments for three⁃dimensional penetrable scatterers[J].JOpt Soc Am A,1994,11:383.
[15] Rao SM,Wilton D R,Glisson AW.IEEE.Electromagnetic scattering by surface of arbitrary shape[J].Trans on Ant Prop,1982,30:409.
[16] AlejandroW R,Alexander PM,David W,Federrico C,Joannopoulos JD,Johnson SG.Bonding,antibonding and tunable optical forces in asymmetric membranes[J].Physical Review Letter,2010,104:160402.
[17] Yang Y P,Zeng R,Chen H,Zhu S Y,Zubairy M S.Controlling the Casimir force via the electromagnetic properties of material[J].Physical Review A,2010,81:022114.
[18] Homer M T.Fluctuating surface currents:A new algorithm for efficient prediction of Casimir interactions among arbitrary materials in arbitrary geometries[D].Massachusetts:Masssachusetts Institute of Technology,2011.
Nonzero⁃point Casim ir Force Between Nano Devices
FANG Ming1,SONG Kaihong1,WANG Juanjuan1,HUANG Zhixiang1,WU Xianliang1,2(1.Key Laboratory of Intelligent Computing and Signal Processing,Ministry ofEducation,Anhui University,Hefei 230039,China;2.Department ofPhysics and Electronic Engineering,Hefei Normal University,Hefei 230061,China)
A frequency domain electromagnetic algorithm boundary element method is applied for computation of Casimir forces between arbitrarymaterialswith arbitrary geometry.Considering electric andmagnetic surface currentdistributions,Casimir force of two objects in terms of interactions of surface currents is obtained.Casimir effects between dielectric objects embedded in dielectric fluid are presented and numerical conditions of repulsive Casimir force are investigated.Non⁃zeropoint energy Casimir force calculation method is provided.It can be used for design of realistic MEMS.
Casimir force;electromagnetic algorithm;nonzero⁃point energy;repulsive Casimir force
O413.2
A
2014-01-15;
2014-06-07
国家自然科学基金(61101064,51277001);安徽省杰出青年基金(1108085J01);教育部新世纪优秀人才基金(NCET⁃12⁃0596);安徽省高校自然科学基金(KJ2011A002,KJ2011A242,KJ2012A013)及教育部博士点基金(20123401110009)资助项目
方明(1990-),男,研究生,从事量子光学中电磁算法研究,E⁃mail:lyqy007@gmail.com
Received date: 2014-01-15;Revised date: 2014-06-07
