二维磁性系统和准一维磁性纳米管的内能
2015-11-30米斌周冯翠菊祁云平薛永红华北科技学院基础部北京060西北师范大学物电学院甘肃兰州730070
米斌周,冯翠菊,祁云平,丁 东,薛永红(.华北科技学院基础部,北京 060;.西北师范大学物电学院,甘肃兰州 730070)
文章编号:1001⁃246X(2015)01⁃0086⁃07
二维磁性系统和准一维磁性纳米管的内能
米斌周1,冯翠菊1,祁云平2,丁 东1,薛永红1
(1.华北科技学院基础部,北京 101601;2.西北师范大学物电学院,甘肃兰州 730070)
采用量子统计理论的多体格林函数法计算二维单离子各向异性海森伯铁磁体、反铁磁体以及单壁铁磁纳米管的内能,对比铁磁体和反铁磁体的结果.在相同的参量下,反铁磁能量总是低于相应的铁磁能量(相变点除外).由于反铁磁能量随温度上升的速度较铁磁能量快,当温度升高到居里点TC和奈尔点TN时(TC=TN),铁磁能量和反铁磁能量相等.横向关联效应对系统内能的影响较大,不能忽略.
海森伯模型;二维系统;磁性纳米管;内能;多体格林函数法
0 引言
近年来,在纳米科技蓬勃发展的背景下,低维磁性材料研究引起了科学家们的极大兴趣.为了研究二维和一维磁性系统的磁化行为和物理机制,人们发展了不同的理论技术方法.文献[1]采用自旋动力学方法研究了磁偶极相互作用表现的边界效应对小尺寸正方形铁磁薄膜的磁化翻转过程的影响,文献[2]采用Monte Carlo模拟对自旋为1/2的一维钻石链反铁磁Ising系统的磁化进行研究,文献[3]采用变分法研究了具有反铁磁界面交换耦合的铁磁/反铁磁双层膜系统中交换偏置场和矫顽力场随冷却场的变化等.在众多的理论方法中,涉及多体格林函数法的研究相对较少.由于多体格林函数法考虑了量子涨落效应[4-12]并且可以从低温到高温统一地处理铁磁理论问题,此方法运用于处理海森伯磁性系统被证明是非常成功的[6-9,12-19],因而具有更加诱人的吸引力.对于一个海森伯磁性系统,人们成功地运用量子统计理论的多体格林函数方法求出磁化强度随温度的变化,有一个对于任意自旋量子数S都适用的普遍公式[4-6].内能是热力学系统的基本物理量.在量子统计力学中,内能就是哈密顿量的系综平均值.文献[7]严格给出了S=1/2,1时铁磁体的内能公式.文献[8]给出了一个铁磁系统对于任意自旋量子数都适用的考虑横向关联函数时比较严格的内能表达式.文献[9]利用多体格林函数方法计算了单壁铁磁纳米管的内能,并与二维平面的情况做了比较.其
实,文献[7-9]都是将海森伯交换相互作用项中的纵向和横向部分放在一起处理的,计算过程较复杂,而且只适用于铁磁系统.文献[7]的近似更严格,只给出了S=1/2,1时铁磁体的内能,对于大的自旋量子数则会涉及到更高阶的格林函数,而且不同自旋量子数的内能公式不统一.本文的做法是将海森伯交换相互作用项中的纵向和横向部分分开成两项分别计算.对于纵向部分(1/2)J,采用无规相近似:≈,(i≠j)[4-5],相应的能量称为纵向平均场能;对于横向部分(1/2)J,利用谱定理[5-6]做严格的计算,相应的能量称为横向关联能.对于简单格子和复式格子都可以计算.既适用于铁磁系统,也适用于反铁磁系统和亚铁磁系统,还适用于单壁磁性纳米管.本文数值计算二维单离子各向异性海森伯铁磁体和反铁磁体的内能.对于铁磁体,包括准一维的单壁铁磁纳米管,将数值结果与文献[8-9]的结果做了比较.自旋量子数较小时(S=1,3/2),接近零温时,文献[8-9]的内能曲线更低.当温度升高时,本文的内能曲线更低.自旋量子数较大时(S=2,5/2,3),在接近零温的低温区,本文与文献[8-9]的计算结果较为一致;温度升高时,文献[8-9]的内能曲线较低.在接近居里点的高温区,本文的内能曲线较低.
1 模型、方法和计算公式
描述一个海森伯磁性体的哈密顿量为

其中,第一项是海森伯交换相互作用项,下标i、j表示格点,Jij表示格点i、j之间的交换积分.本文只考虑最近邻交换作用,求和遍及所有最近邻格点,设最近邻格点间的交换积分Jij=J.J<0表示铁磁交换,J>0则表示反铁磁交换.最近邻格点间的距离设为a.第二项是单离子各向异性项,D是各向异性强度,也称为各向异性场.由于各向同性的海森伯模型在二维和一维情况下是没有自发磁化的[10-11],要加上各向异性项才会出现自发磁化,即低于三维情形时(1)式中的D必须不为零.一般认为D比 |J| 小两个数量级.第三项是有外磁场时的能量.本文设玻尔兹曼常数kB=1,则交换强度J、各向异性强度D、外磁场Bz和温度T等参量都是无量纲的量.本文的数值计算中取:|J |=100,D=1,2,5.
采用多体格林函数法计算二维正方格子单离子各向异性海森伯铁磁体(FM)、反铁磁体(AFM)和单壁铁磁纳米管的内能.要计算该磁性系统的内能,需要先计算出磁化强度.计算磁化强度时,要对高阶格林函数做分解近似,对于海森伯交换相互作用项和单离子各向异性项分别采用了无规项近似[5,15-16](RPA)和Anderson⁃Callen(AC)分解近似[14,20-21].内能是哈密顿量的系综平均值.整个晶体有N个格点.考虑到晶格的平移周期性和对称性,只需要计算出平均每个自旋的能量,以下简称铁磁(或反铁磁)能量,记为E,即
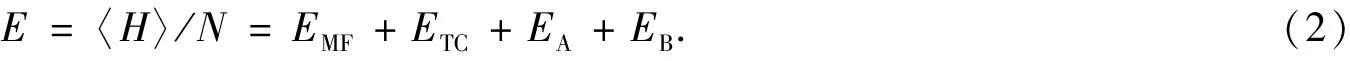
式(2)中的能量包含了四项,其中前两项分别是纵向平均场能EMF和横向关联能ETC,后两项分别是各向异性能EA和外磁场能EB.为了简单起见,本文只计算不加外磁场(Bz=0)时的内能,令EB≡0.为了讨论方便,我们在后面的数值计算中将纵向平均场能、各向异性能之和称为经典能量,计为EC=EMF+EA.用S表示自旋量子数,〈Sz〉表示铁磁体的z分量磁化强度,〈Szμ〉(μ=1,2)分别表示反铁磁体两个子晶格的z分量磁化强度.下面分别给出铁磁、反铁磁能量的计算公式.
1.1 铁磁能量的计算公式
对于铁磁系统,(2)式中的纵向平均场能为

其中,

式(2)中的横向关联能为

其中,

式(6)、(8)中的自旋波能谱为

这里波矢k=(p,q),晶格常数为a.在方程(9)中,
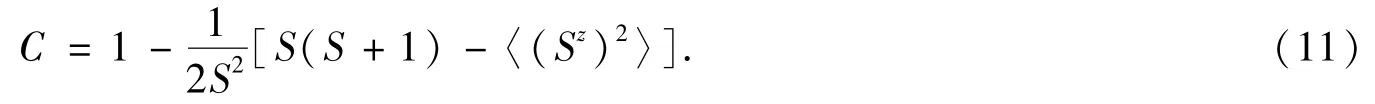
式(2)中的各向异性能为

其中
1.2 反铁磁能量的计算公式
对于反铁磁系统,晶格分成了两个子晶格(复式格子).整个晶体有N个格点,其中两个子晶格各有N/2个格点.无外磁场时,两个子晶格的自发磁化强度大小相等,方向相反,〈〉=-〈〉=-〈Sz〉.式(2)中的纵向平均场能为
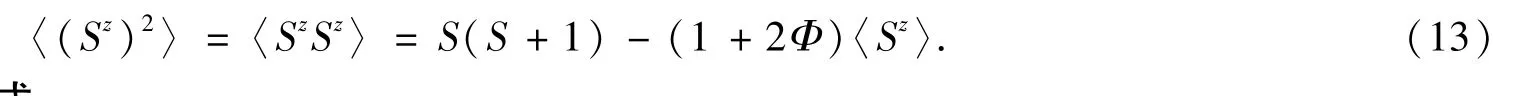

其中
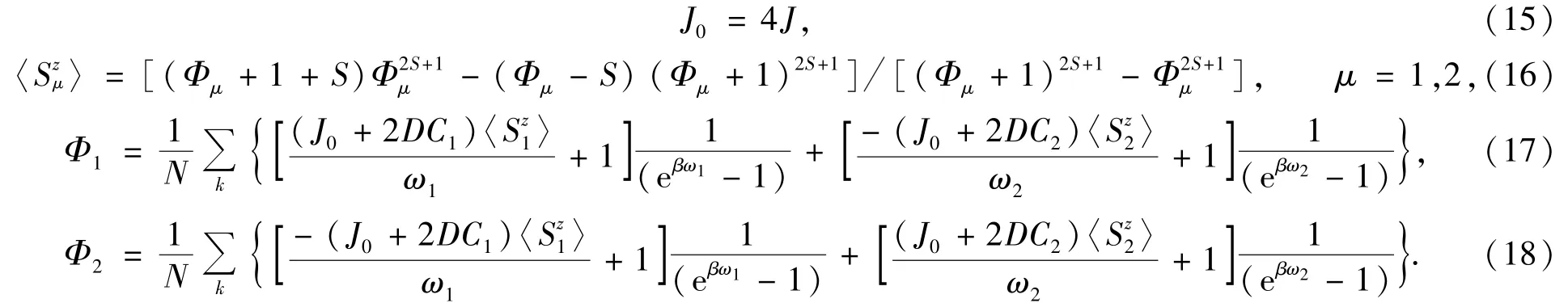
式(17)、(18)中的自旋波能谱分为两支

其中
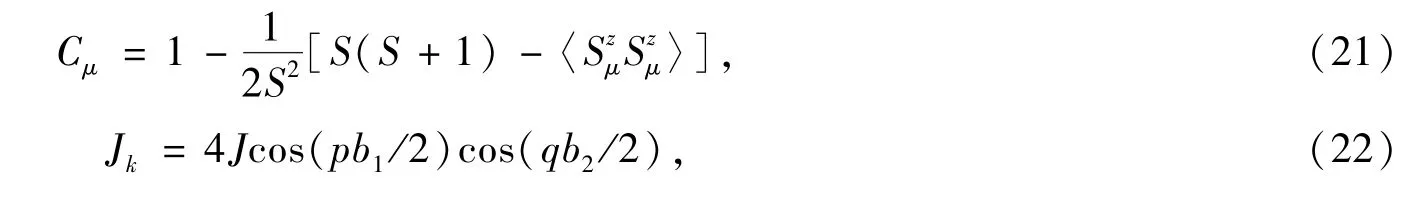
晶格常数b1=b2=2a.式(2)中的横向关联能为
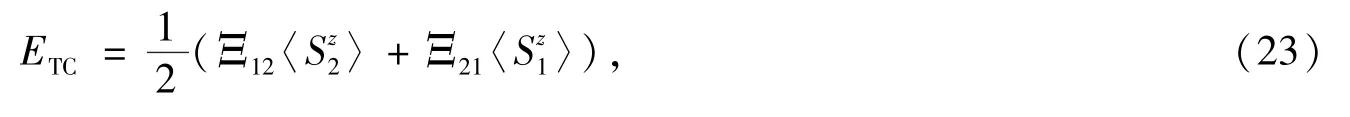
其中
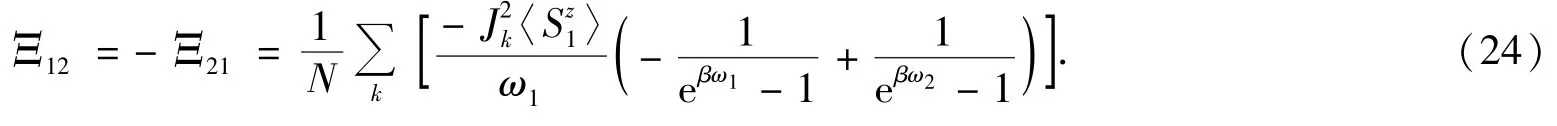
式(2)中的各向异性能为

其中

当S=1/2时,(Sz)2=1/4,即使加上式(1)等号右边的第二项,即单离子各向异性项,也不显现各向异性[8-9,12].因此,计算S=1,3/2,2,5/2,3时的情况.
2 数值结果和讨论
不加外磁场时,将铁磁(或反铁磁)能量分成了两部分:经典能量EC=EMF+EA和横向关联能ETC.图1 (a)、(b)、(c)给出了几个不同自旋量子数(S=1,3/2,2,5/2,3)时铁磁体、反铁磁体的内能随温度的变化,并将二者做了比较.其中,图1(a)是铁磁能量,图1(b)是反铁磁能量,图1(c)将二者对比.可以看出,若自旋量子数一定,在零温时,铁磁能量高于反铁磁能量.温度升高,铁磁能量和反铁磁能量都上升.反铁磁能量随温度上升的速度较铁磁能量更快,当温度升高到居里点TC和奈尔点TN时(这里TC=TN),铁磁能量和反铁磁能量相等.在零温和相变点之间,包括零温,反铁磁能量总是低于铁磁能量.
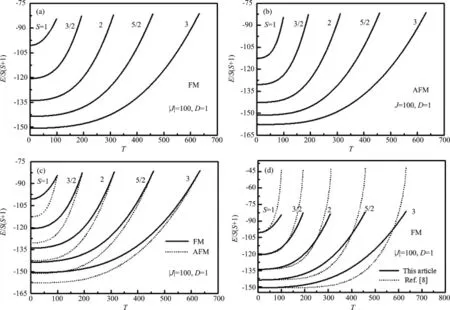
图1 不同自旋量子数(S=1,3/2,2,5/2,3)时:(a)铁磁体(FM)、(b)反铁磁体(AFM)的内能随温度的变化;(c)铁磁能量和反铁磁能量;(d)本文和文献[8](原文图4)的铁磁能量Fig.1 Intrinsic energy versus temperature:(a)FM energy,(b)AFM energy,(c)FM and AFM energies,and(d)FM energies(Spin quantum number S=1,3/2,2,5/2,3.)

此外,我们利用本文的近似方法计算了几个不同自旋量子数(S=1,3/2,2,5/2,3)和管径[9]m=20时铁磁纳米管(FM⁃nanotube)的内能随温度的变化,并与文献[9]的近似作了比较,如图2所示.本文与文献[9]结果差别的主要原因在于能量表达式中近似项的多少,本文的近似项数较少,得到的内能数值更准确一些.在这里需要指出和强调的一点是,本文计算内能的近似方法对于简单格子和复式格子都适用.既适用于铁磁系统,也适用于反铁磁系统和亚铁磁系统,还适用于准一维单壁磁性纳米管.关于亚铁磁体的内能,将会在后续工作中做详细计算.
图3给出了自旋量子数S=2时,铁磁体和反铁磁体的经典能量、横向关联能和内能随温度的变化.其中,图3(a)是铁磁体,图3(b)是反铁磁体.可以看出,经典能量EC和内能E都随温度的升高而升高,横向关联能ETC随温度的升高而降低.三者之间的关系是E=EC+ETC.在某一有限温度处,横向关联能等于经典能量.对于铁磁体,零温时,横向关联能为零,铁磁能量和经典能量相同.这是因为,在零温时,不存在热力学涨落,对于铁磁系统,也不存在量子涨落.对于反铁磁系统,情况大不一样,零温时,横向关联能不为零,铁磁能量低于经典能量.这是因为,在零温时,反铁磁系统存在量子涨落.温度升高,量子涨落和热力学涨落效应出现并逐渐增强,磁化强度减小,铁磁能量和反铁磁能量上升.温度升高到相变点时,对于铁磁系统和反铁磁系统,经典能量都非常接近零,铁磁能量和反铁磁能量分别等于相应的横向关联能.在零温和相变点之间,铁磁能量、反铁磁能量总是低于相应的经典能量,这表明横向关联效应是很重要的,不能忽略.此外,图3表明,在居里点TC和奈尔点TN,铁磁能量和反铁磁能量的数值都不为零.这是因为,在铁磁系统和反铁磁系统中,由于横向关联效应,体系具有某种程度的短程序,这样,在居里点TC和奈尔点TN,即使磁化强度为零,铁磁能量和反铁磁能量也是非零的.
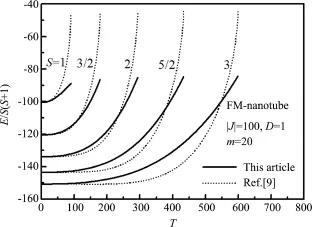
图2 不同自旋量子数(S=1,3/2,2,5/2,3)时铁磁纳米管的内能随温度的变化Fig.2 Intrinsic energy of FM nannotubes versustemperature at several S

图3 (a)铁磁体(FM)、(b)反铁磁体(AFM)的经典能量、横向关联能和内能随温度的变化Fig.3 Longitudinalmean⁃field energy,transverse correlation energy,and intrinsic energy versus temperature:(a)FM,(b)AFM

图4 不同自旋量子数(S=1,3/2,2,5/2,3)时:(a)铁磁体(FM)、(b)反铁磁体(AFM)的横向关联能随温度的变化Fig.4 Transverse correlation energy versus temperature at several S:(a)FM and(b)AFM
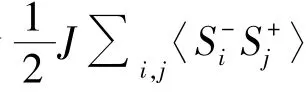

图5 不同各向异性强度(D=1,2,5)时铁磁体(FM)、反铁磁体(AFM)的横向关联能随温度的变化Fig.5 Transverse correlation energy versus temperature (a)FM,(b)AFM
图5给出了几个不同各向异性强度(D=1,2,5)时铁磁体和反铁磁体的横向关联能随温度的变化.参量都相同时,在零温和相变点之间,包括零温,反铁磁体比铁磁体的横向关联能更低.在相同的参量下,铁磁体的横向关联能随温度减小的更快,这样到达相变点(TC=TN)时,铁磁体和反铁磁体的横向关联能相同.可以看出,对于铁磁体在有限温度下和反铁磁体在全温区,横向关联能的绝对值随着各向异性强度D的增大而减小.
本文虽然没有计算加外磁场时的内能,从哈密顿量可以看出,加上外磁场后能量会降低.我们可以推测出,对于铁磁体在有限温度下和反铁磁体在全温区,横向关联能的绝对值随着外磁场Bz的增大而减小.
3 结论
采用量子统计理论的多体格林函数法计算了二维单离子各向异性海森伯磁性体的经典能量、横向关联能和内能,将铁磁体和反铁磁体的结果作了比较.对于铁磁体的内能,包括准一维的单壁铁磁纳米管,将本文的计算结果与文献[8-9]的结果做了比较.主要结论如下:
1)温度升高,铁磁能量和反铁磁能量都上升.参量相同时,在零温和相变点之间,包括零温,反铁磁能量总是低于铁磁能量.由于反铁磁能量随温度上升的速度较铁磁能量更快,当温度升高到居里点TC和奈尔点TN时(TC=TN),铁磁能量和反铁磁能量相等.
2)对于铁磁体的内能,包括单壁铁磁纳米管,我们将本文的数值结果与之前文献的结果做了比较.本文与文献[8-9]结果差别的主要原因在于能量表达式中近似项的多少.由于本文的近似项数较少,因此得到的内能数值更准确.
3)横向关联效应对系统内能的影响较大,不能忽略.对于铁磁体在有限温下和反铁磁体在全温区,横向关联能(数值为负)的绝对值随着自旋量子数S、各向异性场D和外磁场Bz的增大而减小.
[1] Li M,Su Y C,Hu JG.Boundary effects in magnetization reversal ofmicro⁃square ferromagnetic thin films[J].Chinese J Comput Phys,2012,29(2):285-290.
[2] Feng L Y,Xin ZH,WangW T.Magnetic properties of one⁃dimensional antiferromagnetic Ising diamond chain[J].Chinese JComput Phys,2010,27(4):613-618.
[3] Xu X Y,Gu J Y,Meng R N,Li T,Hu J G.Thickness dependence of positive exchange bias in ferromagnetic/antiferromagnetic bilayers[J].Chinese JComput Phys,2011,28(5):786-790.
[4] Callen H B.Green function theory of ferromagnetism[J].Phys Rev,1963,130:890-898.
[5] Tyablikov S T.Methods in the quantum theory ofmagnetism[M].New York:Plenum,1967.
[6] Wang H Y.Green's function in condensedmatter physics[M].Beijing:Science Press and Alpha Science International Ltd,2012. [7] Fröbrich P,Kuntz P J.Many⁃body Green′s function theory of Heisenberg films[J].Phys Rep,2006,432:294-297.
[8] Wang H Y,Xia Q.The total energy of Heisenberg ferromagnetic systems[J].Acta Phys Sin,2007,56(9):5466-5470.
[9] Mi B Z,Wang H Y,Zhou Y S.Theoretical investigations ofmagnetic properties of ferromagnetic single⁃walled nanotubes[J]. JMagn Magn Mater,2010,322(8):952-958.
[10] Mermin N M,Wagner H.Absence of ferromagnetism or antiferromagnetism in one⁃or two⁃dimensional isotropic Heisenberg models[J].Phys Rev Lett,1966,17:1133-1136.
[11] Tao R B,Pu F C.On the absence of the phase transition in a low⁃dimensionalmagnetic system withmulti⁃quadratic exchange interactions[J].Acta Phys Sin,1980,29(5):658-660.
[12] Mi B Z,Wang H Y,Zhou Y S.Theoretical investigations ofmagnetic properties of ferromagnetic single⁃layered nanobelts[J]. Phys Status Solidi B,2011,248(5):1280-1286.
[13] Zheng Q Q,Pu FC.Application of the Green's fuctionmethod to the theory of antiferromagnetism for S≥1/2[J].Acta Phys Sin,1964,20(7):624-635.
[14] Anderson F B,Callen H B.Statisticalmechanics and field⁃induced phase transitions of the heisenberg antiferromagnet[J]. Phys Rev,1964,136:A1068-A1087.
[15] Wang H Y,Zhou Y S,Wang C Y,Lin D L.Investigation of ultra⁃thin ferromagnetic films with a simple cubic lattice[J]. Chin Phys,2002,11(2):167-173.
[16] Wang H Y,Zhou Y S,Wang C Y.Magnetization of coupled ultrathin ferromagnetic films[J].Commun Theor Phys,2002,38:107-112.
[17] Wang H Y,Dai Z H.Quantum statistical calculation of exchange bias[J].Commun Theor Phys,2004,42:141-145.
[18] Xiong Z J,Wang H Y,Ding Z J.Theoretical investigation of exchange bias[J].Chinese Phys,2007,16(7):2123-2130. [19] Xiong Z J,Wang H Y,Ding Z J.Theoretical investigation of exchange bias in compensated cases[J].Commun Theor Phys,2008,50:1241-1244.
[20] Schwieger S,Kienert J,NoltingW.Theory of field⁃induced spin reorientation transition in thin Heisenberg films[J].Phys Rev B,2005,71:024428.
[21] PiniM G,Politi P,Stamps R L.Anisotropy effects on themagnetic excitations of a ferromagnetic monolayer below and above the Curie temperature[J].Phys Rev B,2005,72:014454.
Article ID:1001⁃246X(2015)01⁃0093⁃08
Abstract: Magnetic properties of single⁃wall ZnSnanotubes(NTs)doped with Fe atoms are studied with first⁃principles calculations. Formation energies of doped NTs are smaller than that of pristine one,which indicating that doping is an exothermic reaction. Monodoped NTs has atom⁃likemagnetic momentsmainly due to 3d componentof Fe atoms.It indicates that Fe⁃doped ZnSNTs tend to adopt antiferromagnetic(AFM)configurations.To obtain room temperature ferromagnetism,we replaced an S atom by a C atom and found that C atom prefers to substitute Satom connecting two Fe atoms.Ferromagnetic(FM)state energy is lower than that of AFM state by 164 meV.It implies that room temperature ferromagnetism is expected in these systems.
Key words: codoping;nanotube;magnetic properties;density functional theory
0 Introduction
ZnS is an important II⁃VIcompound semiconductorwith potentialapplications in electronics and optoelectronics due to itswide direct band gaps,3.77 eV for the wurtzite structure[1]and 3.72 eV for the zinc⁃blende structure[2].Nanodimensional ZnS is found to exhibit excellent optical and optoelectronic properties that are remarkably different from the bulk[3-5],making it a versatile building block for nanoscale electronic and photonic devices.
Over the past few years,considerable efforts have been placed on the synthesis of ZnS tubular structures[6-10].Magnetic NTs are interesting and technologically important objects of physical researches with many promising applications of future generations of nanoelectronic devices[11-13]. Previous computations have made on magnetic properties of Mn⁃doped ZnO NTs[14]and transition atom(TM)doped GaN NTs[15].Several theoretical researches have made on the magnetic properties of Mn⁃doped ZnS surfaces[16-17],TM doped ZnSbulk materials[18-20]and ZnSNWs[21]. Our previous work on ZnS NTs focused on the magnetic property of monodoped ZnS NTs[22].To obtained room temperature ferromagnetism,interaction between two TM atomsmust be considered.
In thiswork,we carried outa systematic computational study on Fe⁃doped ZnSNTs.The paper is organized as follows.We first describe computational details in Sec.1 and then present results and discussions in Sec.2.Finally,conclusions are given in Sec.3.
1 Theoreticalmethod and com putational details
The calculations were performed by using spin⁃polarized density functional theory(DFT)asimplemented in the DMOL package[23-24].All electron treatments and double numerical basis set including d⁃polarization functions(DND)were chosen when thismethod was used.The exchange⁃correlation interaction was treated using generalized gradient approximation(GGA)with the functional parameterized by Perdew⁃Burke⁃Ernzerhof correction(PBE)[25].SCF calculations were performed with a convergence criterion of 10-6hartree on total energy.All structures were fully optimized with no symmetry constraint,with a convergence criterion of0.002 hartree·Å-1for forces and 0.005Åfor displacement.Mulliken population analysis[26]was performed to determine charge transfer and magneticmoment on each atomic site.
2 Results and discussions
2.1 Pristine ZnS tube
The pristine ZnSnanotube(P⁃ZnS)with a 1.00 nm diameter is cut from a bulk ZnSalong the [0001]direction.The relaxed structures are shown in Fig.1.Distinct surface relaxation occurred on the facets after geometry optimization.Zn atoms move inward whereas S atoms move outward,forming a buckle of Zn⁃S dimer.
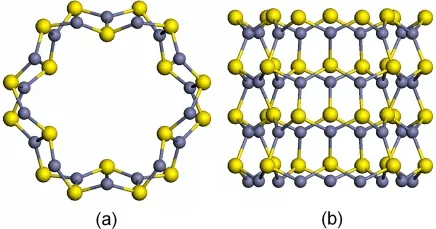
Fig.1 (a)Top⁃view and(b)side view of P⁃ZnSNT(The small and big balls represent Zn and Satoms,respectively.)
2.2 Femonodoped ZnS tube
Since Fe atoms adopt divalent ionic states,they substitute readily for divalent cations. Therefore,only substitutional doping was considered.This scenario has been confirmed by previous experiments[27-28].To achieve realistic experimental doping concentrations(approximately 2% -3%),a super cell that consisted of 36 Zn and 36 S atoms was used,in which one Zn atom is replaced by a Fe atom,named M⁃ZnS.This corresponds to a doping concentration of 2.8%.A structural optimization was subsequently performed for P⁃ZnS.The electronic properties of P⁃ZnS had been calculated in our previous work[22].It has been shown that P⁃ZnS is a direct band gap semiconductor with a band gap(3.52 eV)larger than that of the bulk ZnS(2.23 eV)due to quantum confinement effects.M⁃ZnS was further optimized in this investigation.The optimized structures are plotted in Fig.2(a).We observedminor changes in lattice constants and bond lengths after structural optimization due to the different ionic radii of Zn and Fe atoms.This indicates that Fe atom doping does not change the crystal structure of ZnS NTs,which is in agreement with experimental results[27-28].
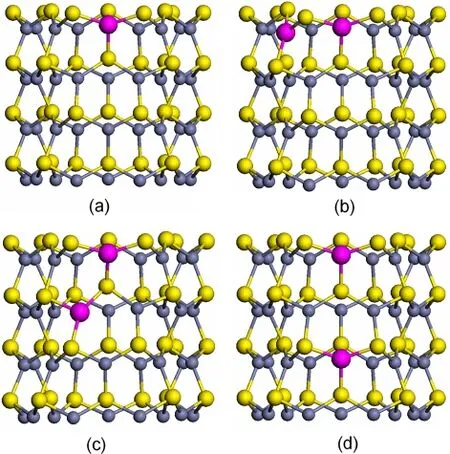
Fig.2 (a)Side⁃view of Femonodoped and(b)to(d)bidoped ZnSNTs(Small,middle,and big balls represent Zn,S,and Fe atom,respectively.)
To compare energy stability of doped ZnSNTs,the formation energy Efwas calculated Ef=Etot-EP-ZnS-n1EFe-n2EC+n3EZn+n4ES,where Etot,EP-ZnS,EFe,EC,EZn,and ESare the total energy of doped NT,the energy of P⁃ZnS,the energy of Fe,C,Zn,and Satom,respectively.n1,n2,n3and n4are numbers of Fe,C,Zn,and S atoms in the doped NTs,respectively.It is known that themore negative the Efis,themore stable a NTwould be.The calculated results are shown in Table 1.The formation energy of doped NT is lower than thatof P⁃ZnSNT,which indicated that the Fe⁃doped NT is exothermic.

Table 1 Formation energy Ef,band gap Ep,local charge QFeand localmagnetic momentμFeof Fe atom,and total magnetic m omentμtotof M⁃ZnS,magnetic moments contributed by the nearest neighboring S and Zn atom sμS,μZn
Electronic properties of M⁃ZnSwere calculated.The band gap is shown in Table 1.Clearly,the band gap of M⁃ZnS is smaller than that of P⁃ZnS(3.52 eV).The band structures of M⁃ZnS alongΓ⁃Z direction are shown in Fig.3.It can be seen that certain localized states existed near Fermi levels,which would make the band gap narrower than that of P⁃ZnS.In addition,M⁃ZnS shows semiconducting characteristic with indirect band gap.These indicate that Fe⁃doping changes significantly electronic properties of P⁃ZnS.

Fig.3 Band structures ofmonodoped ZnSNTs
We performed Mulliken population analysis to determine charge transfer and magnetic moment on each atomic site.Themagnetic properties of doped NT are presented in Table 1.3d electrons of Fe atom followed Hund's rule and maximized the magnetic moment.Our results indicate that the magneticmoment is very close to those of free atom,which suggesting that the defect behaved like an isolated Fe atom at this doping level.This aspect of DMS has been observed previously and explained alongwith the large ferromagnetic exchange splitting of the impurity's defectband[29-30].
An important quantity characterizing the delocalization ofmagnetic moments around Fe atom is induced magnetic moments in surrounding atoms of the host semiconductor.The hybridization between Fe and S atoms plays an important role in the formation of induced magnetic moments. Their magnetic moments have same direction,indicating that Fe atom induces FM interactions between surrounding S atoms(Table 1).Substitutionally doping a Fe atom at a Zn site in ZnSNT changes the number of spin⁃majority or spin⁃minority states in the valence band of ZnS NT.The spin⁃majority states of Fe atom are occupied,and the spin⁃minority states are partially occupied. Thus,the spin⁃majority states in S atoms becomemore occupied than the spin⁃minority states,and the induced magneticmoments in them are parallel to those in Fe atom.Zn atoms interacte with S atoms in the same way as Fe atoms.
2.3 Fe bidoped ZnS tube
In this section,two Zn atoms in a super cell substituted by two Fe atoms is studied formagnetic interaction.We considered three possible configurationswith different spatial positioning of Fe atoms (B1,B2,and B3),respectively.Each was fully relaxed before the magnetic moments were calculated.The optimized structures are plotted in Figs.2(b)-2(d).The distances between two Fe atoms are listed in Table 2.The formation energy and the relative energyΔEr=EFM(AFM)-Egroundstatebetween the AFM (FM)states and the ground state are presented in Table 2.Energy differencesΔE=(EFM-EAFM)between AFM and FM states are also listed in Table 2.
Magnetic properties of all bidoped structures were computed and presented in Table 3.Again,Fe atoms induced FM interactions between surrounding Satoms.
For isomers B3 with a large distance over 5Å,AFM and FM states are degenerate in energy,and have same geometry,local charge,and magnetic moment except that the AFM state has a slightly larger band gap.It means that magnetic coupling between two Fe atoms is short⁃ranged,which has been confirmed by previous researches[31-34].

Table 2 Distances between two Fe atom s dFe,formation energy Ef,band gap Ep,relative stabilityΔEr,and relative energiesΔE=(EFM-EAFM)of Fe⁃bidoped ZnSNTs

Table 3 Local charge QFe1and QFe2and magnetic mom entμFe1andμFe2of two Fe atom s,magneticmoment of thenearest neighboring S atomsμS,and totalmagnetic momentμtot,of Fe⁃bidoped ZnSNTs
The lowest energy configuration B1 is an AFM state where Fe atoms replace two nearest Zn atoms,which implies that Fe atoms have a tendency to form clusters around Ssites.For isomers B1 and B2,the states with AFM coupling are lower in energy than the states with FM coupling.It indicates that Fe⁃doped ZnS NTs tends to adopt AFM configuration.How can we obtain FM coulping?
2.4 Fe/C codoped ZnS tube
Additional hole doping may further promote ferromagnetism.A similar idea was proposed by Huang et al[35]who showed that an acceptor like N codoping in Mn doped ZnSe nanocrystal can induce ferromagnetism.This is because the holesmediate Mn⁃Mn spins.Sharma et al[36]found that C codoping in Mn doped ZnO has room temperature ferromagnetism due to carriers introduced by oxygen vacancies and the substitution of C atO sites.Here,we replaced a Satom by a C atom in Fe doped ZnSNTs.We only considered the configuration that C atom replace a S atom between Fe atoms,named CB1 and CB2.The optimized structures are plotted in Fig.4.After relaxation,the local structure around C dopant shrinks slightly,with Fe atomsmoving closer to C atom.
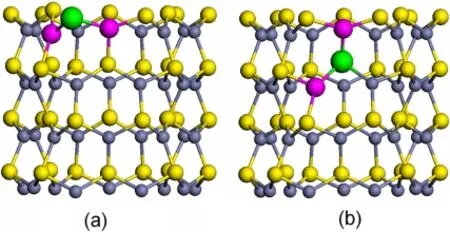
Fig.4 Side⁃view of Fe/C codoped ZnSNTs(The small,middle,big,and huge balls represent S,Zn,Fe,and C atom,respectively.)
Calculated formation energies,relative energies,and energy differences between AFM and FM states are listed in Table 4.After C codoping,all doped NTs show FM coupling.For CB1 configuration,the formation energy of FM state is lower than that of AFM state by 164 meV.Such energy differences imply that room temperature ferromagnetism may be expected in these systems.

Table 4 Totalmagnetic momentsμtot,local charges QFe1,QFe2and localmagnetic momentsμFe1,μFe2andμCof Fe and C atoms,formation energies Ef,relative energiesΔEr,energy differencesΔE of Fe/C codoped ZnSNTs
Mulliken population analysis for charge transfer and magnetic moment on each atomic site of Fe/C codoped ZnS NTs are presented in Table 4.Due to hybridization with C atom,the local magnetic moments of Fe atoms decrease.For CB1 and CB2 configurations,totalmagnetic moments are only 4μBfor FM states.The localmagnetic moment of C atom is always antiparallel to those of neighboring Fe atoms.
3 Conclusions
Structural,electronic,and magnetic properties of ZnS NTs doped with Fe atoms were systematically studied by using first⁃principles calculations.The formation energies of doped NTs are smaller than that of P⁃ZnSNT,which indicating that the process for forming the Fe⁃doped NTs is exothermic.Mulliken population analysis shows that all monodoped ZnS NTs have atom⁃like magnetic moments,which ismainly contributed to the 3d component of Fe atoms.The hybridization between Fe atoms and S atoms playes an important role in the formation of induced magnetic moments.Fe atoms induced FM interactions between surrounding S atoms of the host semiconductor.To obtain ferromagnetism,we replaced a Satom by a C atom.The FM state energies are lower than those of AFM states by 0.164 eV.Such energy differences imply that room temperature ferromagnetism could be expected in these systems.
[1] Ong H C,Chang R P H.Optical constants of wurtzite ZnS thin films determined by spectroscopic ellipsometry[J].Appl Phys Lett,2011,79(22):3612-3614.
[2] Tran T K,Park W,Tong W,et al.Photoluminescence properties of ZnS epilayers[J].JAppl Phys,1997,81(6):2803-2809.
[3] Wang Y W,Zhang L D,Liang C H,et al.Catalytic growth and photoluminescence properties of semiconductor single⁃crystal ZnS nanowires[J].Chem Phys Lett,2002,357(3-4):314-318.
[4] Dinsmore A D,Hsu D S,Gray H F,et al.Mn⁃doped ZnS nanoparticles as efficient low⁃voltage cathodoluminescent phosphors[J].Appl Phys Lett,1999,75(6):802(1-3).
[5] Denzler D,Olschewski M,Sattler K.Luminescence studies of localized gap states in colloidal ZnS nanocrystals[J].JAppl Phys,1998,84(5):2841-2845.
[6] Wang X D,Gao P X,Li J,et al.Rectangular porous ZnO⁃ZnS nanocables and nanotubes[J].AdvMater,2002,14(23):1732-1735.
[7] Zhou T Y,Xin X Q.Room temperature solid⁃state reaction—A convenient novel route to nanotubes of zinc sulfide[J].Nanotechnology,2004,15(5):534-536.
[8] Shen X P,Han M,Hong JM,et al.Template⁃based CVD synthesis of ZnS nanotube arrays[J].Chem Vapor Depos,2005,11(5):250-253.
[9] Yin LW,Bando Y,Zhan J H,et al.Self⁃assemble highly faceted wurtzite⁃type ZnS single⁃crystalline nanotubeswith hexagonal cross⁃sections[J].Adv Mater,2005,17(14):1972-1977.
[10] Zhai T Y,Gu Z J,Ma Y,et al.Synthesis of ordered ZnS nanotubes by MOCVD⁃template method[J]. Mater Chem Phys,2006,100(2-3):281-284.
[11] Zutic I,Fabian J,Sarma SD.Spintronics:Fundamentals and applications[J].Rev Mod Phys,2004,76 (2):323-410.
[12] Fu L,Cao L C,Zhu D B.Molecular and nanoscalematerials and devices in electronics[J].Adv Colloid Interface Sci,2004,111(3):133-157.
[13] Lu J G,Chang P C,Fan Z Y.Quasi⁃one⁃dimensional metal oxide materials⁃Synthesis,properties and applications[J].Mater Sci Eng R,2006,52(1-3):49-91.
[14] He A L,Wang X Q,Fan Y Q,et al.Electronic structure and magnetic properties of Mn⁃doped ZnO nanotubes:An ab initio study[J].JAppl Phys,2010,108(8):084308(1-5).
[15] Chen G X,Zhang Y,Wang D D,et al.Structural,electronic and magnetic properties of the 3d transition metal⁃doped GaN nanotubes[J].Solid State Communications,2011,151(2):139-143.
[16] Li L,LiD,Liu SY,et al.Electronic properties of Mn doping ZnS(001)surfaces[J].Chinese JComput Phys,2010,27(2):293-298.
[17] Song DW,Niu Y,Xiao L,et al.Structural,electronic,and magnetic properties of Mn⁃doped ZnS(110)surfaces:First⁃principles study[J].Chinese JComput Phys,2012,29(2):277-284.
[18] Stern R A,Schuler T M,MacLaren JM,et al.Calculated half⁃metallic behavior in dilute magnetically doped ZnS[J].JAppl Phys,2004,95(11):7468-7470.
[19] Tablero C.Electronic and magnetic properties of ZnS doped with Cr[J].Phys Rev B,2006,74(19):195203(1-9).
[20] McNorton R D,Schuler T M,MacLaren JM,et al.Systematic trends of first⁃principles electronic structure computations of Zn1-xAxB diluted magnetic semiconductors[J].Phys Rev B,2008,78(7):075209(1-11).
[21] Chen H X,Shi D N,Qi J S.Comparative studies on magnetic properties of ZnS nanowires doped with transition⁃metal atoms[J].JAppl Phys,2011,109(8):084338(1-9).
[22] Chen H X,Liu C L.Stability,electronic and magnetic properties of ZnS nanotubes:A comparative study [J].Chinese JComput Phys,2013,30(1):148-158.
[23] Delley B.An all⁃electron numericalmethod for solving the local density functional for polyatomic molecules [J].JChem Phys,1990,92(1):508-517.
[24] Delley B.From molecules to solids with the DMol3approach[J].JChem Phys,2000,113(18):7756-7764.
[25] Perdew JP,Burke K,ErnzerhofM.Generalized gradient approximationmade simple[J].Phys Rev Lett,1996,77(18):3865-3868.
[26] Mulliken R S.Electronic population analysis on LCAO⁃MO molecular wave functions.II.Overlap populations,bond orders,and covalent bond energies[J].JChem Phys,1955,23(10):1841-1846.
[27] Yuan H J,Yan X Q,Zhang Z X,et al.Synthesis,optical,and magnetic properties of Zn1-xMnxS nanowires grown by thermal evaporation[J].JCryst Growth,2004,271(3-4):403-408.
[28] Kang T,Sung J,Shim W,et al.Synthesis and magnetic properties of single⁃crystalline Mn/Fe⁃doped andco⁃doped ZnS nanowires and nanobelts[J].JPhys Chem C,2009,113(14):5352-5357.
[29] Himpsel F J.Exchange splitting of epitaxial fcc Fe/Cu(100)versus bcc Fe/Ag(100)[J].Phys Rev Lett,1991,67(17):2363-2366.
[30] Orteg JE,Himpsel F J.Inverse Photoemission from V,Cr,Mn,Fe,and Co monolayers on Ag(100)[J].Phys Rev B,1993,47(24)16441-16446.
[31] Wang Q,SunQ,Jena P.Ferromagnetism in Mn⁃doped GaN nanowires[J].Phys Rev Lett,2005,95 (16):167202(1-4).
[32] Schmidt T M,Venezuela M P,Arantes J T,et al.Electronic and magnetic properties of Mn⁃doped InP nanowires from first principles[J].Phys Rev B,2006,73(23):235330(1-5).
[33] Schmidt T M.Surface effects on the energetic and spintronic properties of InP nanowires diluted with Mn:First⁃principles calculations[J].Phys Rev B,2008,77(8):085325(1-6).
[34] Ghost S,Wang Q,Das G P,et al.Magnetism in ZnO nanowire with Fe/Co codoping:First⁃principles density functional calculations[J].Phys Rev B,2010,81(23):235215(1-10).
[35] Huang X,Makmal A,Chelikowsky J R,et al.Size⁃dependent spintronic properties of dilute magnetic semiconductor nanocrystals[J].Phys Rev Lett,2005,94(23)236801(1-4).
[36] Sharma V K,Najim M,Varma G D.Effect of carbon co⁃doping on the magnetic properties of bulk Mn doped ZnO[J].JMagn Magn Mater,2011,323(24)3198-3201.
Intrinsic Energies of Two⁃dimensional Heisenberg M agnets and Ferromagnetic Single⁃walled Nanotubes
MIBinzhou1,FENG Cuiju1,QIYunping2,DING Dong1,XUE Yonghong1
(1.Department of Basic Curriculum,North China Institute ofScience and Technology,Beijing 101601,China;2.College of Physics and Electronic Engineering,Northwest Normal University,Lanzhou 730070,China)
Intrinsic energy of two⁃dimensional square lattice single⁃ion anisotropic Heisenberg ferromagnets,antiferromagnets,and ferromagnetic single⁃walled nanotubes are calculated withmany⁃body Green's functionmethod in quantum statistical theory.Calculated results of ferromagnets and antiferromagnets are compared.Between zero temperature and phase transition point,including zero temperature,anti⁃ferromagnetic energy is always lower than that of ferromagnetic energy.Calculationmethod of intrinsic energy in this paper is applicable not only to ferromagnetic system,butalso suitable for antiferromagnetic system and ferrimagnetic system,aswellas ferromagnetic single⁃walled nanotubes.Intrinsic energies are greatly lower than classical energies,which shows that transverse correlation effect is important.
Heisenbergmodel;two⁃dimensional systems;magnetic nanotubes;intrinsic energy;many⁃body Green's functionmethod
M agnetic Properties of Single⁃wall ZnS Nanotubes Doped w ith Fe Atom s
XIE Jianming,CHEN Hongxia
(College of Physical Science and Electronic Techniques,Yancheng Teachers University,Yancheng 224002,China)
O469 Document code:A
O469
A
2013-12-28;
2014-06-03
收稿日期:2014-01-06;修回日期:2014-06-17
中央高校基本科研业务费专项资金(3142012017)、河北省教育厅科技基金(A2013024)和河北省高等学校科学技术研究项目(QN2014330)资助项目
米斌周(1980-),男,硕士,讲师,博士生,主要利用多体格林函数法进行磁性材料的理论计算,E⁃mail:mbzfjerry2008@126.com
Received date: 2014-01-06;Revised date: 2014-06-17
Received date:2013-12-28;Revised date:2014-06-03
Foundation item s:Supported by Natural Science Foundation of China(11247235,11404279)and Qinglan Project of Jiangsu Province
Biography:Xie Jianming(1976-),male,major in first⁃principles calculations of structure and property ofmaterials,E⁃mail:dtxiejianming@sina.com
