纤维缠绕复合材料气瓶内衬的屈曲分析

付 敏，林 松，陈 亮，周文龙

(1.大连理工大学材料科学与工程学院，大连 116023;2.航天材料及工艺研究所，北京 100076)

复合气瓶通常由金属内衬和复合材料增强层共同组成［1］.此类气瓶继承了复合材料比强度和比刚度高、抗疲劳性能好等诸多优点［2］，可明显提高压力容器的可靠性、安全性、承载能力、使用寿命，并能大大减小压力容器的质量［3-4］.

由于复合气瓶内衬厚度较小，在一定压应力状态下会发生屈曲，因此确定临界失稳外压是复合气瓶结构设计中十分重要的任务.王荣国等［5］采用简化模型，分析了超薄内衬复合材料压力容器在卸载过程中由内衬压应力导致的内衬屈曲现象，并验证其模型分析的可靠性.左惟炜等［6］对三维编织复合材料圆柱壳进行屈曲分析，计算了高压储气瓶的临界失稳载荷.Cai等［7-8］结合有限元法和水压屈曲试验研究，结果表明，复合材料的纵向弹性模量和缠绕层厚度在很大程度上影响复合气瓶的失稳行为.Moon等［9］对中等壁厚的复合材料气瓶在外部静水压力下的屈曲和破坏特性进行了研究，并成功预测了屈曲外压.

复合气瓶的制备通常采用纤维缠绕法［10］，缠绕张力影响复合材料层的纤维含量和气瓶的失效强度［11-14］.研究表明，一定大小的缠绕张力才能使复合材料层发挥作用［15］，缠绕张力越大，越有利于提高复合气瓶的疲劳寿命，减小气瓶质量［16-17］.然而，在制备过程中若缠绕张力过大，会导致内衬发生屈曲失稳而破坏.

本文建立了复合气瓶内衬结构的有限元模型，将复合材料层对内衬的缠绕张力等效为均匀分布的外压力，通过逐渐增大外压力，分析计算内衬的临界失稳外压，为复合气瓶制备过程中缠绕张力的选择提供参考依据.利用特征值屈曲分析得到了内衬1～10阶的屈曲模态，再采用非线性稳定法计算出临界失稳外压的精确值.通过将计算结果与内衬外压试验结果进行对比分析，验证数值模拟的可靠性.

1 有限元模型的建立

1.1 几何参数

本文计算的复合气瓶内衬的容积为56 L，全长462 mm，由封头、筒身以及与外部连接的接头组成.内衬封头段为椭球形，筒身段壁厚1.3 mm，内径400 mm，外径402.6 mm.

1.2 单元划分

对于本文研究的复合气瓶，考虑铝合金内衬在自紧压力下会发生塑性变形，内衬选择采用SOLID186实体单元.SOLID186单元是高阶的三维20节点结构实体单元，每个节点有3个自由度，单元具有塑性、大变形和大应变能力.

为保证网格质量，选用扫掠法对几何体进行网格划分.内衬共划分为9 408个实体单元、66 860个节点.图1为内衬网格划分后的有限元模型轴截面图.

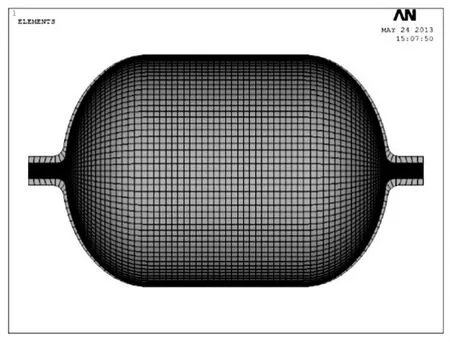
图1 内衬有限元模型的轴截面图

1.3 材料属性

复合气瓶内衬材料为各向同性的6061-T6铝合金，其主要性能参数见表1.

表1 6061-T6铝合金内衬的主要性能参数

1.4 边界条件

复合气瓶的边界条件是由其实际约束条件和加载方式决定的.根据研究对象的实际工作环境，本文在模型的底端面实施固支约束，即气瓶底端固定，顶端面施加径向、切向位移约束，只允许有轴向位移.

1.5 求解过程

屈曲是指结构件在承受逐渐增加的载荷时，突然出现位移迅速增大，而载荷基本保持不变的力学行为，当应力-位移曲线出现水平段时，可认为该结构件发生了屈曲.ANSYS软件对于屈曲载荷和屈曲模态的预测有两种方法:特征值屈曲分析和非线性屈曲分析.前者仅考虑弹性行为，后者真实地考虑实际结构的塑性行为和大挠度等情况，可真实地跟踪失稳过程，与工程实际相近.

特征值屈曲分析的平衡方程为

式中:K为刚度矩阵，S为应力刚度矩阵，λi为载荷乘子，qi为位移特征向量.

使式(1)有非0解的条件为

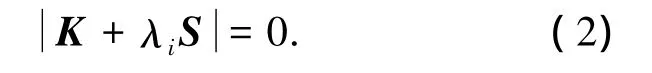
由此可见，屈曲问题是一个求解特征值的过程，对于有n个自由度的模型，产生λ的n阶多项式，本文只计算前10阶特征值.

非线性屈曲分析的控制方程为

式中:KT为某一增量步的切线刚度矩阵，Δu为位移增量，ΔP为载荷增量.在分析过程中，为保证分析结果的准确性，载荷增量必须以很小的速率增加.

本文利用特征值屈曲分析方法计算得出复合气瓶内衬的1～10阶屈曲模态，初步预测内衬的临界失稳外压和屈曲发生位置.由于无缺陷模型不会发生屈曲，因此将前10阶模态的位移量作为几何缺陷引入模型，采用非线性稳定法精确计算出内衬临界失稳外压.内衬各阶模态最大位移量为1 mm，筒身外壁半径为201.3 mm.为使位移缺陷大小与制造公差(小于筒身外壁半径的1%)在同一量级，因此选取前10阶模态叠加位移量的比例因子为0.1.

2 模拟结果及试验分析

2.1 模拟结果分析

通过特征值屈曲分析得到复合气瓶内衬的1～10阶屈曲模态，图2为各模态的形状.内衬在发生屈曲时，筒身段出现向内凹陷和向外凸起现象，而封头段较完好，说明屈曲破坏发生在筒身段.前10阶模态的临界失稳外压如表2所示，第1阶模态下内衬的临界失稳外压为0.191 MPa，表明外压由零增大到此压力时内衬首次发生屈曲.

图2 内衬1～10阶模态

表2 各阶模态下内衬模型的临界失稳外压pMPa

由于特征值屈曲分析仅考虑气瓶内衬的弹性行为，采用此方法得到的模拟结果不够准确，只能对下一步分析提供参考.将前10阶模态的位移量叠加后乘以比例因子0.1作为几何缺陷引入模型，运用非线性稳定法精确计算内衬模型临界失稳外压.

图3为屈曲时内衬模型径向位移量云图，位移量最大值位于筒身段，封头段较完好，因此确定筒身段为内衬屈曲破坏的位置，此结果与特征值法所得结论一致.

图3 内衬径向位移云图

在模型中选取径向位移最大的节点，得到该节点位移随外压的变化情况如图4所示.由图4可知:当外压由0逐渐增大时，节点位移呈线性增加;当外压增大到0.199 MPa时，节点位移急剧增加，而外压几乎保持不变，此临界值0.199 MPa即为内衬临界失稳外压.

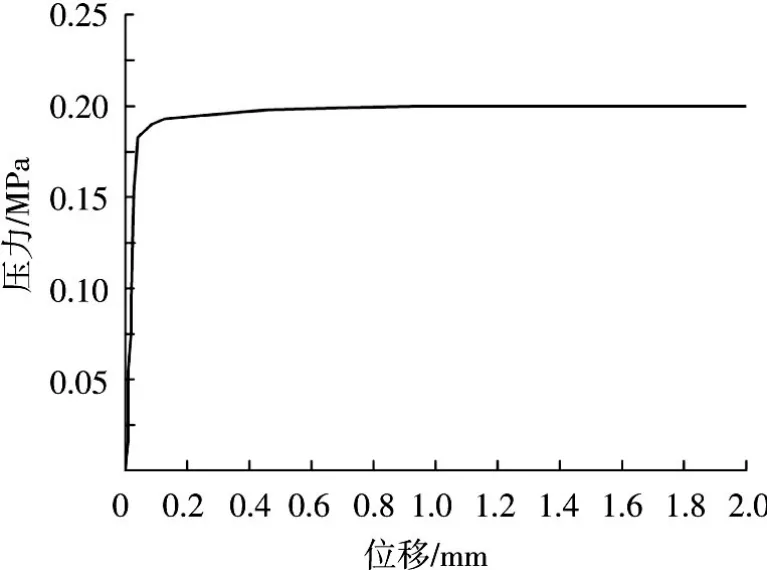
图4 内衬位移量随外压的变化曲线

2.2 外压试验验证

纤维缠绕法制备复合气瓶时，在缠绕过程中对内衬施加缠绕张力，张力的施加要以不使内衬发生屈曲为前提，并且缠绕张力要逐层递减，以保证每组缠绕层的纤维处于等张力状态，充分发挥纤维缠绕层的强度.由于复合气瓶内衬壁厚较小，筒身段仅为1.3 mm，为避免纤维缠绕过程中内衬发生屈曲，利用外压试验确定内衬所能承受的临界失稳外压.图5(a)为外压试验装置示意图，在试验过程中，对内衬逐级施加外压，当载荷增加至0.206 MPa时，听到内衬发出爆破的响声，试验终止.拆除试验装置后检查内衬已经发生屈曲破坏.内衬的屈曲情况如图5(b)和(c)所示，在内衬筒身段出现向内凹陷和向外凸起现象，并沿纵向产生裂纹，内衬封头段较为完整未损坏.产生此现象的原因是筒身段壁厚较小，仅为1.3 mm，而封头段壁厚逐渐过渡到3～5 mm，筒身段壁厚的急剧减薄使其成为内衬的薄弱环节，最终导致屈曲破坏的发生.

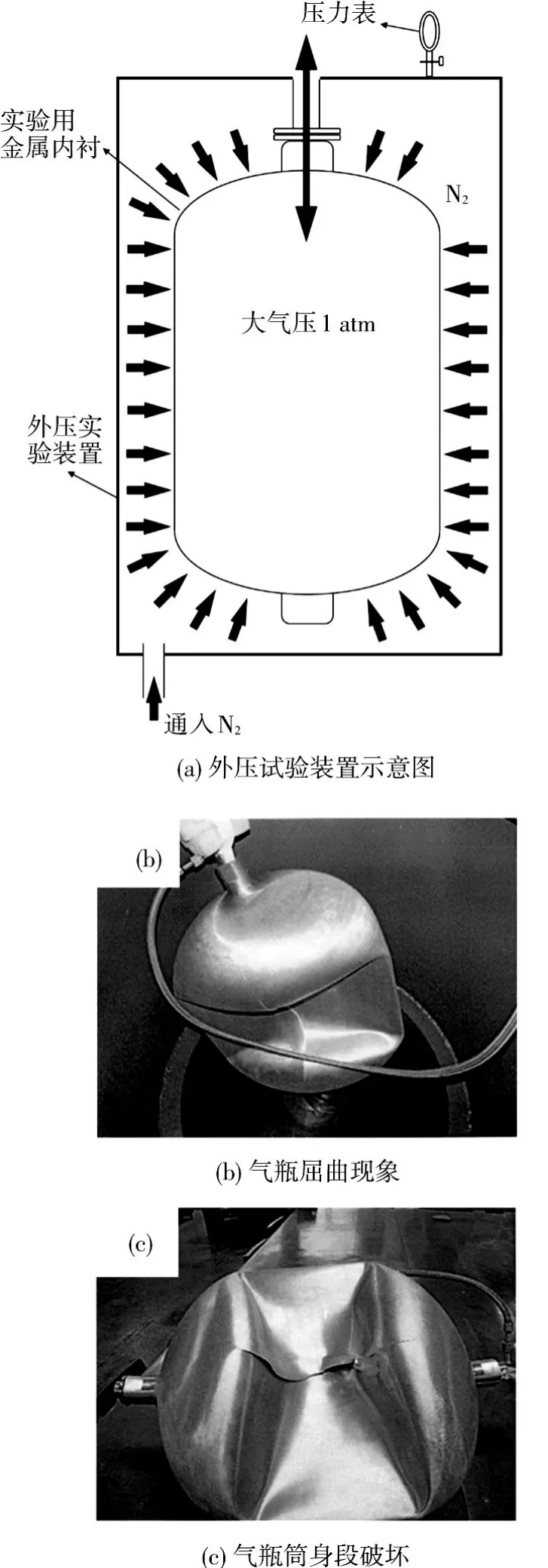
图5 内衬外压试验图

通过对比内衬屈曲发生位置和临界失稳外压，可以认为模拟结果与试验结果基本吻合.由于内衬已完成屈曲变形过程并进一步折皱断裂破坏，根据爆破声确定临界失稳外压的方法所得到的数值，会略高于真实的临界失稳外压，因此，有限元模拟的计算值应该略低于此法的测试值.

3 结 论

1)利用特征值屈曲分析得到复合气瓶内衬的1～10阶屈曲模态形状，并采用非线性稳定法绘制出内衬位移量随外压的变化曲线，计算出内衬临界失稳外压为0.199 MPa;

2)通过将模拟计算的内衬临界失稳压力与内衬外压试验的测试值进行分析比较，显示模拟计算结果与试验测试相符合.

［1］ FRIAS C，FARIA H，FRAZÃO O，et al.Manufacturing and testing composite overwrapped pressure vessels with embedded sensors［J］.Materials and Design，2010，31(8):4016-4022.

［2］ 孙直，任明法，陈浩然.含金属内衬的复合材料缠绕薄壁容器自紧设计的工程方法［J］.复合材料学报，2011，28(2):217-221.SUN Zhi，REN Mingfa，CHEN Haoran.An engineering algorithm autofrettage technique for composite overwrapped［J］.Acta Materiae Compositae Sinica，2011，28(2):217-221.

［3］ PENG Xiongqi，REHMAN Z U.Textile composite double dome stamping simulation using a non-orthogonal constitutive model［J］.Composites Science and Technology，2011，71(8):1075-1081.

［4］ 陈达，肇研，罗云烽，等.循环湿热环境下碳纤维复合材料界面性能［J］.材料科学与工艺，2012，20(6):1-6.CHEN Da，ZHAO Yan，LUO Yunfeng，etal.Interfacial property of carbon fiber composites in cyclic hygrothermal environment［J］.Materials Science and Technology，2012，20(6):1-6.

［5］ 王荣国，赫晓东，胡照会，等.超薄金属内衬复合材料压力容器的结构分析［J］.复合材料学报，2010，27(4):131-138.WANG Rongguo，HE Xiaodong，HU Zhaohui，et al.Structure analysis of composite pressure vessel with ultra-thin metallic liner［J］.Acta Materiae Compositae Sinica，2010，27(4):131-138.

［6］ 左惟炜，肖来元，廖道训.三维编织复合材料筒压储气瓶的屈曲分析与优化设计［J］.中国机械工程，2007，18(3):286-291.ZUO Weiwei，XIAO Laiyuan，LIAO Daoxun.Buckling analysis and optimum design of 3D-braided composites CNGV［J］.China Mechanical Engineering，2007，18(3):286-291.

［7］ CAI Baoping，LIU Yonghong，LIU Zhengkai，et al.Probabilistic analysis of composite pressure vessel for subsea blowout preventers［J］.Engineering Failure Analysis，2012，19:97-108.

［8］ CAI Baoping，LIU Yonghong，LIU Zhengkai，et al.Reliability-based load and resistance factor design of composite pressure vessel under external hydrostatic pressure［J］.Composite Structure，2011，93:2844-2852.

［9］ MOON C，KIM I，CHOI B，et al.Buckling of filament-wound composite cylinders subjected to hydrostatic pressure for underwater vehicle applications［J］.Composite Structure，2010，92:2241-2251.

［10］ WANG Rongguo，JIAO Weicheng，LIU Wenbo，et al.Slippage coef fi cientmeasurementfornon-geodesic fi lament-winding process［J］.Composites:Part A，2011，42(3):303-309.

［11］ COHEN D.Influence of filament winding parameters on composite vesselquality and strength ［J］.Composites Part A: Applied Science and Manufacturing，1997，28(12):1035-1047.

［12］ KEMPNER E A，HAHN H T.Effect of radial stress relaxation on fiber stress in filament winding of thick composites［J］.Composite Manufacturing，1995，6(2):67-77.

［13］ ZHAO Liyang，MANTELL S C，COHEN D，et al.Finite elementmodelingofthefilamentwinding process［J］.Composite Structures，2001，52(3/4):499-510.

［14］ MERTINY P，ELLYIN F.In fl uence of the fi lament winding tension on physical and mechanical properties of reinforced composites［J］.Composites:Part A.2002，33(12):1615-1622.

［15］ ENGLISH S A，ARAKEREA N K，ALLEN P A.J-Q characterized stress fi elds of surface-cracked metallic liners-II.Composite overwrapped pressure vessels［J］.Engineering Fracture Mechanics，2011，78(10):2097-2114.

［16］ 王斌，金志浩，丘哲明，等.树脂含量对芳纶纤维/环氧复合材料性能的影响［J］.固体火箭技术，2002，25(1):61-64.WANG Bin，JIN Zhihao，QIU Zheming，et al.Effect of resin content on properties of aramid fiber/epoxy composites［J］.Journal of Solid Rocket Technology，2002，25(1):61-64.

［17］ 张宗毅，邓贵德，寿比南，等.缠绕张力对环缠绕复合材料气瓶应力的影响［J］.压力容器，2011，28(5):7-14.ZHANG Zongyi，DENG Guide，SHOU Binan，et al.Effect of winding tension on stress of hoop-wrapped composite cylinders［J］.Pressure Vessel Technology，2011，28(5):7-14.