超声波热量表流量计量中温度补偿算法研究*

崔晓志，王 翥

(哈尔滨工业大学（威海）信息与电气工程学院，山东威海264209)

超声波热量表流量计量中温度补偿算法研究*

崔晓志，王 翥*

(哈尔滨工业大学（威海）信息与电气工程学院，山东威海264209)

针对超声波热量表采用时差法测量流量时，因受温度影响而存在的非线性问题，提出了分别基于曲面拟合和BP神经网络的温度补偿算法。两种算法通过建立温度与流量之间的非线性映射关系，达到补偿流量测量的目的。建模与仿真可知，BP神经网络补偿算法表现出更好的数据融合及预测能力。验证实验表明，相对于现有查表修正算法和曲面拟合补偿算法，BP神经网络补偿算法补偿效果更佳，补偿后流量测量误差在±2.2%以内，绝对误差方差最大值为0.68，补偿效果显著，具有较高的工程应用价值。

超声波热量表；BP神经网络；曲面拟合；温度补偿

时差法超声波热量表通过超声检测技术测量流量，进而计算出热量，因此流量测量是决定超声波热量表计量精确度的关键环节［1］。目前，针对如何提高超声波热量表流量测量精确度的问题，国内外学者开展了大量研究。文献［2］中对超声波测量管道内径及超声波换能器安装倾角等参数进行优化，通过减小管道内压力损失提高流量测量的准确性。文献［3］中通过对超声波换能器进行配对测试和标定零点误差，降低自身结构影响，解决了零点漂移问题。文献［4-5］中基于流体力学修正原理和仿真实验，提出各流场下流量修正方法，改善了流量测量误差。但以上研究并未考虑温度对整个流量测量过程的影响。文献［6］中根据超声波传播速度受温度影响的特性，提出软件校正方法，但忽略了管道内流场受温度的影响。文献［7］通过神经网络对15℃～50℃内流量数据进行理论补偿，但训练数据有限且未进行现场实验验证。

针对上述问题，在分析了温度对流量测量影响的基础上，提出了分别基于曲面拟合算法和BP神经网络的温度补偿算法。经建模仿真和现场实验可得，BP神经网络补偿算法能够达到各流量段流量误差要求，补偿性能稳定，对提高流量测量精确度具有显著意义。

1 超声波热量表流量测量误差分析

1.1 时差法流量测量原理

基于时差法的U型反射式超声波热量表流量测量原理如图1所示。

图1 U型时差法流量测量示意图

在U型管道上下游处分别布置换能器A和换能器B，间距为L。换能器发射的超声波经反射面反射后实现信号的收发。测量管道内径为D，换能器与反射面中心间距为D/2。设流体静止时，超声波传播速度为c，流体流速为v0。顺流时，换能器A发射超声波到换能器B接收的时间为t1；逆流时，换能器B发射超声波到换能器A接收的时间为t2。受流体流速影响t1小于t2，超声波顺向和逆向传播时间分别为［8］：

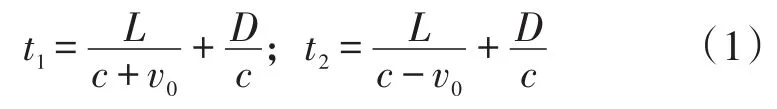
由于c≫v0，整理得流体流速v0为：

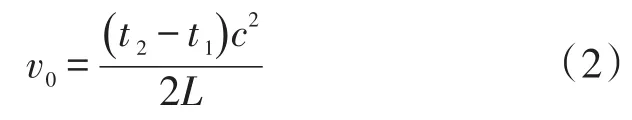
流速v0为轴心线流速，与面流速v成比例关系，即K=v/v0，K为流量修正系数。则体积流量V为：

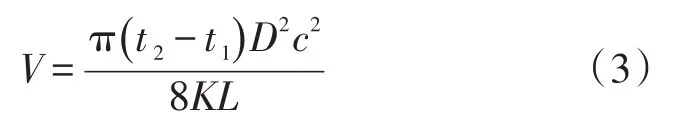
1.2 温度对超声波传播速度影响

由式（3）可得，流体体积流量与超声波传播速度平方成线性关系，而超声波传播速度受流体温度影响具有非线性特点。通过拟合温度与超声波传播速度值，得到不同温度下超声波传播速度曲线［3］，如图2所示。

图2 不同温度下超声波传播速度曲线

随着流体温度的升高，超声波传播速度非线性特征愈发明显。在0～100℃范围内超声波传播速度差值可达152.8 m/s，对应流量测量误差为22.98%，不容忽视。

1.3 温度对管道内流场分布影响

非理想状态下，流体存在粘滞性而具有两种流动状态：流体质点做有条不紊的运动、彼此不相混掺的状态为层流；流体质点做不规则运动、轨迹混乱的状态为紊流［8］。工程中以雷诺数Re标定管道内流体分布状态：当Re＜2 000时，主要受粘性力作用，流体处于层流状态；当Re≥2 000时，主要受惯性力作用，流体处于紊流状态。层流与紊流分布如图3所示。

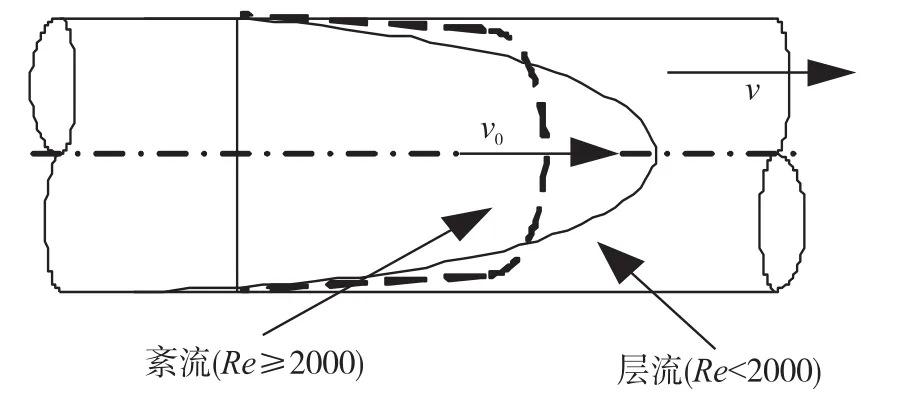
图3 层流与紊流分布图

依据经验公式，流量修正系数K选取原则为：

层流： K=v/v0=0.5;

紊流： K=v/v0=0.75～09。

在5℃～95℃工作条件下，受温度影响Re具有非线性特性。单纯考虑K系数的不同，在25℃时，Re=1 115对应层流；在80℃时，Re=2 725对应紊流［9］，由温度变化所引起的流量测量误差为25.8%，难以避免。

此外，随流体温度变化，管道内压力、管壁粗糙度等因素会产生不确定变动，对流量的测量造成不同程度的影响。因此，在分析温度对流量测量影响的基础上，采取温度补偿流量测量措施具有很大必要性。

2 流量检定实验及分析

2.1 实验设备

热量表检测台是提供确定量值的计量器具，如图4所示，可用于检定超声波热量表流量测量的精确度。

超声波热量表实物如图5所示。检测台流量测量精确度为0.000 1 m3/h，温度测量精确度为0.1℃；超声波流量表型号：DN20，测量量程为0～5.0 m3/h。

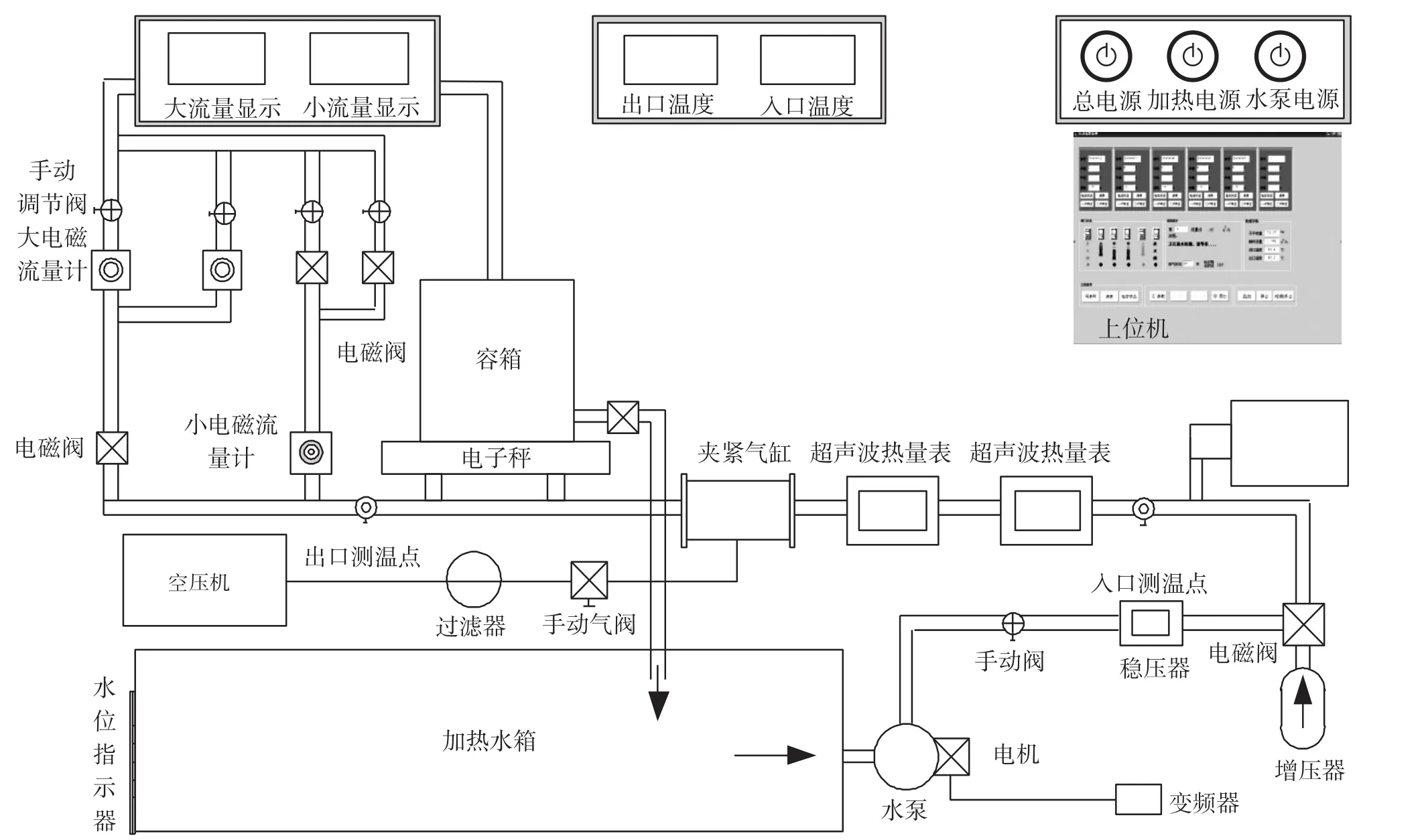
图4 热量表检测台结构图

图5 超声波热量表实物图

结合热量表工作原理，实验中使用启停质量法采集流量测量数据。热量表检定规程中定义的流量测量误差计算公式为：

式中：Vc为超声波热量表记录的流量值，L；ms、mf分别为阀门在开关前后容箱的质量，kg；ρt为检定时流体密度，kg/m3。

2.2 实验方案

本次实验是为验证温度对超声波热量表流量测量的影响，同时提供温度补偿流量算法建模所需数据。

针对中小流量测量误差情况复杂，较难进行补偿，则主要对0～2.9 m3/h流量区进行温度补偿研究。实验中测量的温度点和流量点分别如表1和表2所示。

表1 实验温度点

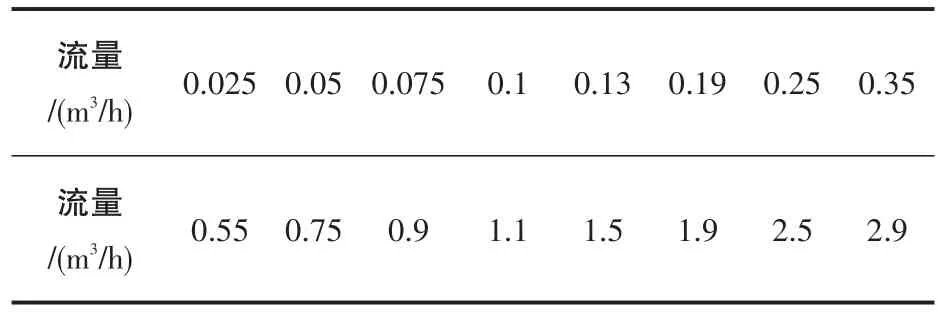
表2 实验流量点

根据热量表检定规程，各温度、流量点下进行3次实验，分别记录112种工况下的温度值、实际流量值、测量流量值、流量测量误差值，取平均作为终值。

2.3 实验数据分析

整理实验采集的测量数据，温度对流量测量影响如图6所示（由于数据量巨大，篇幅有限，不再粘附）。

图6 不同温度下流量测量误差曲线

结合检定实验数据及图6分析可得以下结论：

①流量测量精确度与流量大小相关

在0～0.5 m3/h流量段内流量测量误差范围为45.31%～10.76%，流量测量误差及误差变化率相对较大；在0.5 m3/h～2.9 m3/h流量段内流量测量误差范围为16.94%～8.3%，随流量增大，测量误差及变化率均减小。

②流量测量精确度受温度影响

在20℃～50℃低温区内流量测量误差范围为45.31%～8.51%，流量测量误差随温度变化有较大波动，小流量点处较明显；在60℃～80℃高温区内流量测量误差范围为16.37%～8.3%，流量测量误差受温度影响减小并趋于一致。

为此，考虑建立网络化温度补偿流量算法模型，补偿温度对流量测量的影响，提高流量测量精确度。

3 温度补偿算法建模及仿真测试

3.1 建模及仿真测试方案

针对流量测量误差受温度影响特性，分别采用曲面拟算法和BP神经网络建立网络化温度补偿模型，实现温度、测量流量与实际流量间的非线性映射。

考虑到流量测量误差变化率的差异，对［0～0.6 m3/h］和［0.4 m3/h～2.9 m3/h］高低两个流量区域分别进行补偿算法建模。仿真测试及实验验证时，测量流量以0.5 m3/h流量点为高低流量区分界点。

实验采集的数据分为标准数据和测试数据，其中0.1 m3/h、0.25 m3/h、0.75 m3/h、1.9 m3/h流量点作为测试数据。建模中引入0.0 m3/h的测量流量值和实际流量值，以提高补偿模型的数据融合能力。同时，每个温度点使用其临近的采集温度点所对应的数据，如56℃下使用60℃所采集实验数据。

3.2 曲面拟合算法

曲面拟合算法利用最小二乘拟合曲线原理，通过拟合不同温度下的实际流量和测量流量数据，得到温度对任意测量区间内所测流量点的网络化补偿模型。该二元二次曲面拟合补偿模型表达式为：

式中：x为温度，℃；y为测量流量，m3/h；z为预测流量，m3/h；p20、p11、p02、p10、p01、p00为待确定系数。

该二元二次模型的误差平方和规范化表达式为：

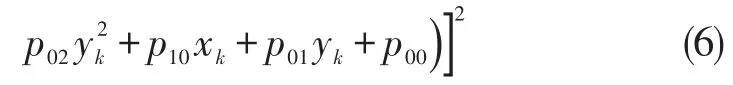
式中：Zk为第k次测量所对应实际流量，m3/h；N为输入样本数。

根据最小二乘原理可得，该问题需求解6元函数Q(p20,p11,p02,p10,p01,p00)的极值问题，即满足：

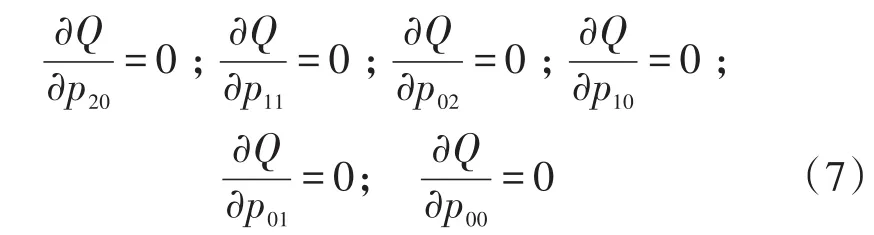
联立式（7），根据高斯法［10］解得高低流量区域内曲面拟合补偿模型的待确定系数，如表3所示。

表3 曲面拟合补偿模型待确定系数

低流量区的拟合度达0.999 9，和方差为1.989×10-4；高流量区的拟合度达0.999 9，和方差为2.844×10-4，均达到预期目标。将采集温度范围和高低流量区分别55等分，结合式（5）和表3数据进行温度补偿算法建模。曲面拟合补偿模型预测效果如图7、图8和图9所示。

图7 低流量区曲面拟合补偿模型预测效果图

由以上仿真测试数据分析可得，基于最小二乘曲面拟合的温度补偿模型能够拟合和预测大部分标准数据和测试数据，但小流量点处流量误差波动性相对较大，预测效果不佳，共存在11个流量点误差超过±2.5%，即误差流量点。总体上达到了温度补偿流量测量目的。

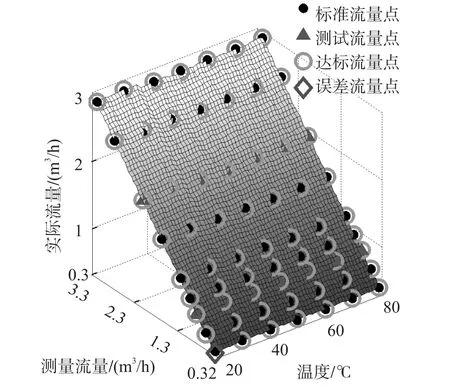
图8 高流量区曲面拟合补偿模型预测效果图

图9 曲面拟合补偿模型预测流量误差曲线

3.3 BP神经网络

BP神经网络是建立在最速下降法基础上的多层前馈网络，由输入层、隐含层和输出层组成［11］。理论证明，含有一个隐含层的BP神经网络可以任意精度逼近任何连续非线性函数。BP神经网络结构如图10所示。

图10 BP神经网络结构图

传统BP神经网络，在追求误差平方最小目标函数过程中易陷入局部极小值。因此，采用附加动量法修正网络中的权值和阈值，可以跳过误差曲线局部极小值，寻找全局最优解，提高BP神经网络预测性能。附加动量法权值调节公式为：

式中：k为迭代运算步数；η(k)为第k步的学习率；mc( ∈[0,1])为动量因子。

该算法将上时刻权值修正量通过动量因子mc引入本次调整中，利用“惯性效应”避免误差目标函数陷入局部极小值问题［12］。

训练过程中动量因子mc选取原则：

mc为零时，权值修正执行最速下降法；mc为1时，权值修正与上次修正相同，忽略最速下降调整量。引入动量因子mc时，当网络权值进入误差曲面底部平坦区域时，Δw(k)变化较小，即w(k+1)≈w(k)，可避免因w(k+1)=0而带来局部极小值的影响。采用附加动量法修正网络阈值过程同理。

基于BP神经网络的温度补偿算法模型包含一个隐含层，共有13个隐含层单元。设置训练步数为200，误差平方和为1×10-4。在MATLAB环境下使用trainbpm.m函数进行神经网络训练，同时设定预测流量值与实际流量值误差在±2.5%以内，确保预测流量的精确性。

低流量区经过29步训练达到目标误差9.86×10-5，拟合度为0.999 99；高流量区经过44步训练达到目标误差9.9×10-5，拟合度为0.999 99，均达到预期目标。提取网络中权值和阈值进行温度补偿算法建模。BP神经网络补偿模型预测效果如图11～图13所示。

图11 低流量区BP神经网络补偿模型预测效果图

图12 高流量区BP神经网络补偿模型预测效果图

图13 BP神经网络补偿模型预测流量误差曲线

由以上仿真测试数据分析可得，基于BP神经网络的温度补偿模型可以融合所有参与训练的标准数据和预测所有测试数据，流量误差均有效控制在±2%以内。经对比，BP神经网络补偿模型预测效果更佳，低流量区流量误差波动性明显降低，流量预测性能稳定。

4 现场实验验证及数据分析

4.1 温度补偿算法移植

为验证温度补偿算法的准确性和实用性，分别提取曲面拟合补偿算法的核心参数和BP神经网络补偿算法的权值、阈值。在IAR WorkBench平台上，通过C语言编程将温度补偿算法移植入超声波热量表程序内，实时补偿流量测量。曲面拟合补偿算法补偿原理如图14所示。

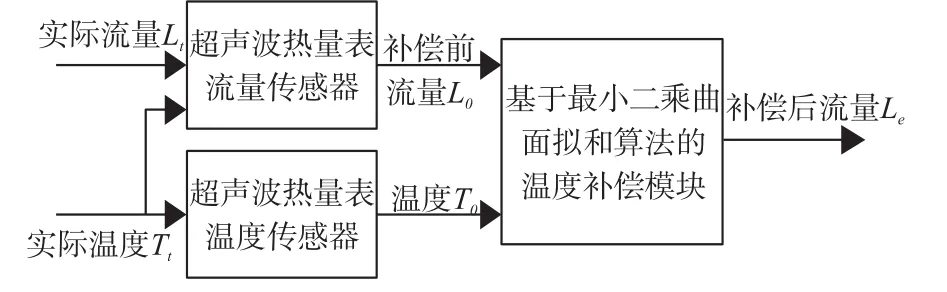
图14 曲面拟合补偿算法补偿原理

工作时，超声波热量表根据补偿前流量选择高低流量区温度补偿模型，结合所测温度进行数据预测，进而输出预测后的流量值，完成温度补偿流量过程。BP神经网络补偿算法补偿原理如图15所示。

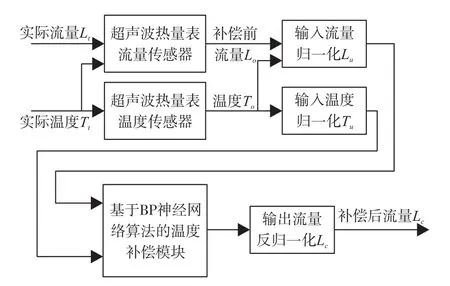
图15 BP神经网络补偿算法补偿原理

BP神经网络补偿算法在补偿过程中需根据采集的温度选择测量流量的归一和反归一边界值；根据测量流量选择高低流量温度补偿模型。对流量进行归一化处理后进行网络预测，然后对预测值进行反归一处理得到预测流量值，完成温度补偿流量过程。

4.2 实验验证及数据分析

实验中引入了现有的查表修正算法做参考。验证实验中分别采集三种算法对应的实际流量、测量流量及流量测量误差。实验中测量的温度点和流量点分别如表4和表5所示。

表4 实验测量温度点

表5 实验测量流量点

实验数据采集及处理过程同2.2节。整理实验数据，得到的三种算法补偿效果分别如图16～图18和表6所示。

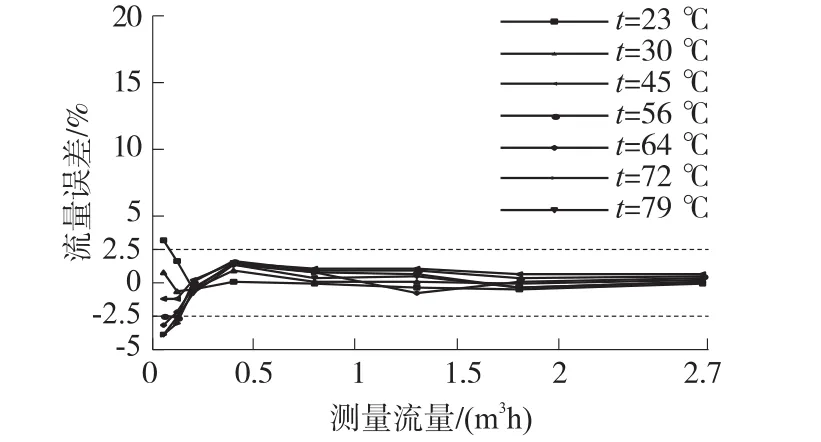
图16 查表修正算法校正后流量测量误差曲线

图17 曲面拟合补偿算法补偿后流量测量误差曲线

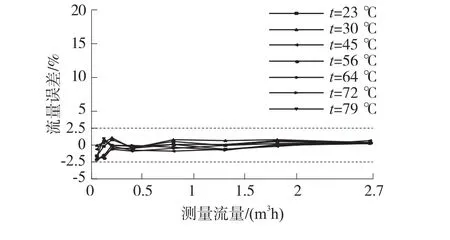
图18 BP神经网络补偿算法补偿后流量测量误差曲线

表6 三种算法对比

通过以上实验数据对比可得，三种算法在一定程度上均可降低温度对流量测量的影响。查表修正算法校正后的流量测量误差在±4%以内，绝对误差平均值最大为1.52%，最大绝对误差方差为3.57；曲面拟合补偿算法补偿后的流量测量误差在±5.5%以内，绝对误差平均值最大为1.36%，最大绝对误差方差为1.99；BP神经网络补偿算法补偿后的流量测量误差在±2.2%以内，绝对误差平均值最大为0.84%，最大绝对误差方差为0.68。

根据《热量表》（CJ128-2007）行业标准中对各流量段测量误差要求，BP神经网络补偿算法能够有效抑制温度对超声波热量表流量测量的影响，补偿效果显著，达到2级表标准。

5 结论

①通过理论和实验数据分析得，超声波热量表流量测量受温度影响较大，存在不可忽视的误差。

②针对流量测量误差受温度影响、且具有非线性这一特点，提出了分别基于曲面拟合算法和BP神经网络的温度补偿流量算法。仿真测试表明，两种补偿算法均能够降低流量测量误差，其中BP神经网络补偿算法具有更稳定的流量预测能力。

③开展验证实验，对比分析三种算法的补偿和校正效果，确定基于BP神经网络的温度补偿算法性能优于其他两种算法，具有较强的流量补偿能力和较高的工程应用价值。

［1］Choi H M，Yoon B R，Kim C G，et al.Evaluation of Flowmeters for Heat Metering［J］.Flow Measurement and Instrumentation，2011，22(5)：475-481.

［2］Wang B，Cui Y，Liu W，et al.Study of Transducer Installation Effects on Ultrasonic Flow Metering Using Computational Fluid Dynamics［C］//Advanced Materials Research.2013，629：676-681.

［3］姚滨滨.智能超声波热量表的开发与研究［D］.浙江大学，2012.

［4］Liu M，Sun L，Hou Y，et al.Ultrasonic Flow Detection and Research on Regression Analysis Calibration Method［C］//2012 International Conference on Systems and Informatics(ICSAI).IEEE，2012：491-494.

［5］陈子静，朱小良.一种基于广义回归神经网络的超声波流量传感器系数求解方法［J］.传感技术学报，2015，28(1)：56-61.

［6］Mingwei L，Guosheng L，Yanguo H.Research on Improving the Accuracy of the Ultrasonic Flow-Meter with Time Difference Method［C］//2010 International Conference on Electrical and Control Engineering(ICECE).IEEE，2010：1704-1707.

［7］李志浩.基于神经网络的超声波流量测量及温度补偿系统的研究［D］.青岛科技大学，2010.

［8］王翥，崔晓志，侯春雷.超声波传感器接收信号强度非对称性分析及对策［J］.传感技术学报，2015，28(1)：81-85.

［9］耿介，周春丽，杜广生，等.关于超声波热量表准确度检测的几个问题［C］//第二十五届全国水动力学研讨会暨第十二届全国水动力学学术会议文集(下册).2013.

［10］Kumar J，Shunmugam M S.Fitting of Robust Reference Surface Based on Least Absolute Deviations［J］.Precision Engineering，2007，31(2)：102-113.

［11］孙凌逸，黄先祥，蔡伟，等.基于神经网络的无线传感器网络数据融合算法［J］.传感技术学报，2011，24(1)：122-127.

［12］Yu F，Xu X.A Short-Term Load Forecasting Model of Natural Gas Based on Optimized Genetic Algorithm and Improved BP Neural Network［J］.Applied Energy，2014，134：102-113.

崔晓志（1990-），男，河北邯郸人，哈工大（威海）信电学院硕士研究生。研究方向为传感器及检测技术；

王 翥（1963-），男，辽宁丹东人，通信作者，哈工大（威海）教授，主要研究方向为无线传感器网络、信号检测与处理、传感器及应用技术，wangzhu@hit.edu.cn。

Research on Temperature Compensation Algorithm in Ultrasonic Heat Meter Flow Measurement*

CUI Xiaozhi，WANG Zhu*
(Harbin Institute of Technology at Weihai，School of Information and Electrical Engineering，Weihai Shandong 264209，China)

When using transit-time ultrasonic heat meter for the flow measurement，there is a nonlinear problem affected by temperature.In order to solve it，this paper proposed two kinds of temperature compensation algorithms respectively based on curve fitting algorithm and BP neural network.These two algorithms compensated flow measurement by establishing mapping relationship between temperature and flow.After modeling and simulation analysis，BP neural network compensation algorithm showed better ability of data integration and prediction.Spot test proved that BP neural network compensation algorithm had superior correction effect than the existing look-up table correction algorithm and curve fitting compensation algorithm.Flow measurement error was limited within±2.2%and the maximum absolute error variance was 0.68 after BP neural network compensating.BP neural network compensation algorithm had great value of application with significant compensation effect.

ultrasonic heat meter；BP neural network；curve fitting；temperature compensation

TB941；TB937

A

1004-1699(2015)08-1169-07

��7820；7320W

10.3969/j.issn.1004-1699.2015.08.012

项目来源：山东省科技发展计划项目（2010GGX10132）；山东省科技发展计划项目（2012GGX10110）；山东省科技发展计划项目（2013GGX10129）

2015-04-09 修改日期：2015-05-28