MEMS光纤法珀压力传感器的设计及解调方法实现*

曹 群，贾平岗*，熊继军，张海瑞，洪应平，房国成

（1.中北大学电子测试技术国家重点实验室，太原030051；2.中北大学仪器科学与动态测试教育部重点实验室，太原030051）

MEMS光纤法珀压力传感器的设计及解调方法实现*

曹 群1，2，贾平岗1，2*，熊继军1，2，张海瑞1，2，洪应平1，2，房国成1，2

（1.中北大学电子测试技术国家重点实验室，太原030051；2.中北大学仪器科学与动态测试教育部重点实验室，太原030051）

基于外界压力引起敏感膜片形变导致腔长变化来实现压力信号传感的原理，提出了一种MEMS光纤法珀压力传感器的设计，建立了传感器敏感膜片的挠度变化与膜厚、半径及施加压力的关系理论模型，并在此基础上进行了膜片的MATLAB二维数值仿真和Comsol Multiphysics三维数值仿真，并完成了FP压力敏感头的制作，进而设计了能够应用于光纤传感的解调方法，搭建了光纤传感的压力测试系统并进行了相关实验，利用所设计的解调方法对实验数据进行处理，进而对压力传感器的性能及特性进行了测试和验证。实验结果表明，传感器测试曲线线性度良好，与数值仿真结果基本一致，在100 kPa的量程范围内其灵敏度可达62.3 nm/kPa，温度敏感系数为0.023 μm/℃，测量精度3.93%，且最小压强分辨率为1.29 kPa，证实了该MEMS光纤法珀压力传感系统具有一定的可行性。

光纤传感；法珀腔；MEMS工艺；解调方法；MATLAB；Comsol Multiphysics

作为各类控制装置及系统信息获取与传输的核心器件，压力传感器及其相关技术的迅速发展，使得各个领域的自动化程度越来越高。与传统的电学压力传感器相比，光纤压力传感器具有抗干扰能力强、动态测试范围宽、高分辨率、体积小且易于多路复用或分路感应等优点，因而在航空、航天、电子等领域中都得到了广泛使用［1-2］。同时，随着以微电子、微机械加工与封装技术巧妙结合的MEMS技术不断发展，利用MEMS技术制造的光纤压力传感器以其重量轻、功能强，具有频带宽和灵敏度高的特性，并且与集成电路工艺兼容能够批量生产，更是成为了当下研究和开发的热点［3-5］。其中，光纤法珀传感器具备结构简单紧凑、受环境波动影响不大、对感应信号衰落不敏感、分辨率高和灵敏度高等优点，已广泛应用于各种物理、化学和生物医学参数的检测及对于压力、温度、流速等的实时系统监测。常用的解调方法有强度解调和相位解调两种，其中，强度解调法容易实现，所需成本低，但由于多采用波长固定的单色光源，其光强容易受光源波动的影响，因而传感精度比较低。相位解调法主要分为条纹计数法、傅里叶变换法、离散腔长变换法及菲索干涉仪法［6-8］，条纹计数法利用光纤法珀传感器的输出干涉条纹和相位的关系来获取传感器的腔长，不会受到光源波动的影响，可以提高传感系统整体的测量精度与稳定性。因此，针对光纤法珀压力传感器的原理，设计了一种MEMS光纤法珀压力传感器，提出了一种基于MOI-sm125光纤光栅解调仪的光纤法珀压力传感器的解调原理及方法，建立了MEMS光纤法珀传感系统的理论模型并完成了关键部位的MEMS工艺制作，进行了相应的数值仿真模拟及实验测试，并对测试数据进行了分析。

1 传感器的设计及基本原理

光纤F-P压力传感器的具体结构如图1所示。

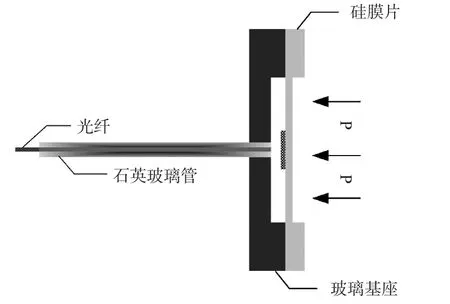
图1 光纤法珀压力传感器结构图

传感器主要包括传感头、石英玻璃管和单模光纤三大部分，其中传感头由硅敏感膜片、玻璃基座和金属反射膜层三部分组成。该传感头利用MEMS工艺制成，通过石英玻璃管辅助准直与光纤粘接构成F-P压力传感器的主体。光源发出的入射光通过光纤耦合进入传感器内，其中，硅膜片表面涂覆的金属层作为法珀腔的一个反射面，石英管中内插光纤的端面作为另一个反射面，光线在F-P腔体的上下表面来回反射，形成多光束干涉，部分反射光沿着原路返回，相遇后再次发生干涉。干涉信号与腔长L有关，当膜片受到外界压力时会沿着轴向产生形变，导致法珀腔腔长变化，从而引起干涉信号发生变化。通过测量干涉信号的变化则可推导出腔长变化，最终进行解调得到压力信息变化数值，实现压力传感。

在小挠度情况下，根据弹性力学原理，硅敏感膜片受到压力后变形情况如式（1）：

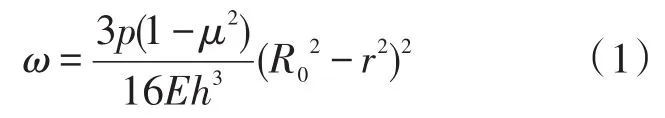
式中：ω为硅敏感膜片挠度；p为敏感膜片所受压力；μ为泊松比；E为硅的杨氏模量；h为敏感膜片厚度；R0为膜片半径；r为膜片任意部位的半径。

对应灵敏度表达式为：

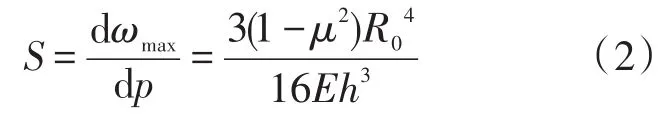
可见压强测量灵敏度与敏感膜的有效半径的4次方成正比，与膜片厚度的3次方成反比，在膜片材料选定后，压强测量灵敏度由膜片的厚度和半径大小决定。薄膜半径越大，厚度越小，膜片灵敏度越高。

光线进入光纤后垂直入射到法珀腔中，在腔内来回多次反射形成干涉。若要保证敏感膜片受到外界施加压力发生形变后仍符合法珀腔的理论模型，那么膜片中心区域的移动必须在实验误差范围内看作是平动，从而敏感膜中心区域的上下移动就可表征法珀腔深度的变化。由于所设计的为圆形敏感膜片，因此选取受压后经过中心点的一个横截面为研究对象（如图2所示）。

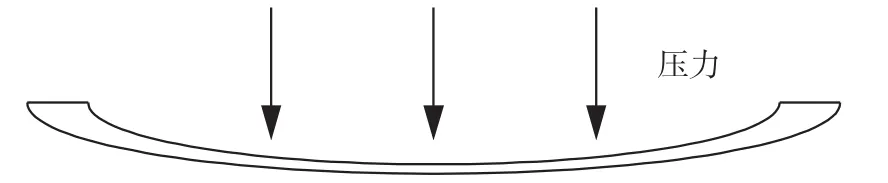
图2 敏感膜片受压后变形的截面图

任何物体在一个平面内的运动都可以由平动加转动组成，如果横截面的每一小的曲线段在一个平面内没有转动或者转动非常小，那么也就证明每一小的曲线段在这个平面的运动只有平动即膜片中心区域的上下移动是平动［9］。为了得到图2中每个小曲线段的斜率的绝对值，首先将式（1）中的ω对距离硅膜中心点的位置r求导：

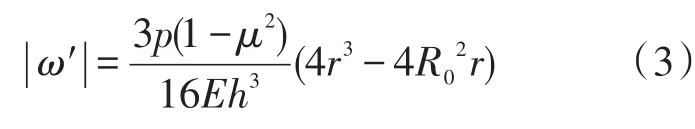
式中，|ω′|指的是图2所示膜片在截面中的每一点上切线的斜率的绝对值，表示了截面中膜片每一点转动角的大小。再将ω′对r求导得：

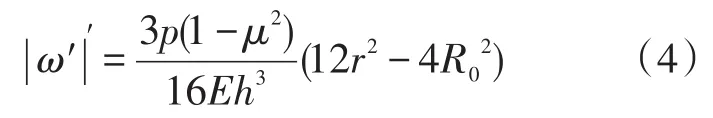
2 数值模拟仿真

敏感膜片的厚度和半径是传感器设计与制作中的主要参数，其参数值选取的不同将直接影响到传感器的性能。当外界施加压力一定时，干涉光强的大小主要由膜片厚度决定，而敏感膜片的半径又在很大程度上决定了传感器的压力测试量程。首先，利用MATLAB软件对光纤传感的理论模型进行仿真分析［10］，分别固定膜片半径、膜片厚度及外界压力值，得到了传感器中各个物理量与膜片挠度变化的关系曲线。

图3是不同半径下的膜片挠度变化与膜厚的关系曲线。

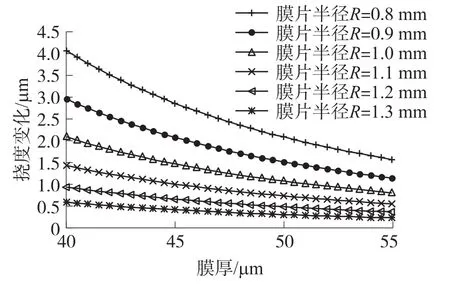
图3 不同半径下，挠度变化与膜厚的关系曲线

设定杨氏模量E=1.9×1011，泊松比μ=0.278，压力值P=100 kPa，从图中可以明显地看出，随着膜片厚度从40 μm增加到55 μm的过程中，膜片挠度变化量呈逐渐递减的趋势，即随着膜厚的增加，膜片的形变量越来越不明显。同时，分别对膜片半径R取0.8 mm、0.9 mm、1.0 mm、1.1 mm、1.2 mm、1.3 mm的6种情况进行计算，可以知道挠度变化量随着膜片半径的增大而增大，即半径越大，膜片的形变越明显。

图4是膜片厚度不同时，挠度随压力的变化曲线。图中至上而下，膜片厚度分别取30 μm、35 μm、40 μm、45 μm、50 μm、55 μm、60 μm，膜片半径R为1.3 mm，可以看出当压力在0～100 kPa之间连续变化时，膜片的挠度变化量逐渐增大，同时，随着膜片越来越薄，其形变也愈加明显。

图4 不同膜厚下，挠度变化与压力的关系曲线

图5为灵敏度与膜片半径及膜片厚度的三维变化曲线。敏感膜片的灵敏度与膜片的半径成正比关系，而与膜片厚度成反比关系，即若要取得较高的膜片灵敏度，应适当的增加膜片半径，同时减小膜片厚度，只有设计出合适的尺寸并确定恰当的参数，才能得到良好的传感器性能。

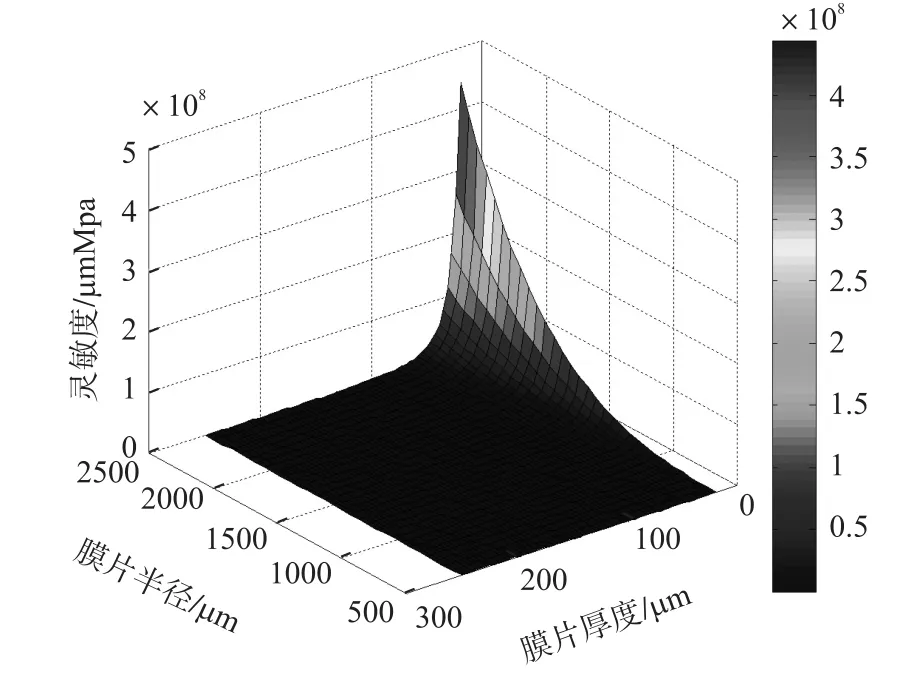
图5 灵敏度与膜片半径及厚度的三维关系图

为了更加直观的观察敏感膜片在受到均匀分布的外部压力后产生形变的状态与实时变化，选用Comsol Multiphysics软件对膜片进行三维仿真分析。膜片中心部分的偏移同时表征了法珀腔腔体长度的变化，进而可以转化得到压力信息，实现压力传感。根据式（1）可模拟得到如图6所示的硅敏感膜片受到不同压力后产生的形变情况。

图6 膜片挠度分布（单位：μm）

3 传感器制作

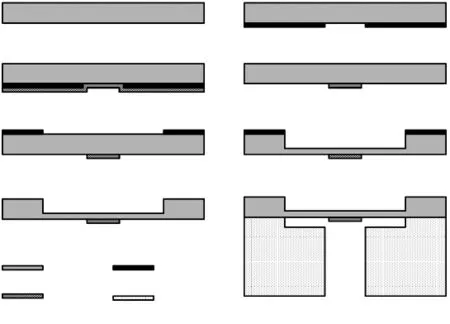
图7 制作工艺流程图

光纤法珀压力传感头的MEMS制作工艺流程如图7所示。该传感器制作采用4英寸的硅片作为衬底，初始厚度300 μm，晶向为＜100＞。制作前经过标准的RCA清洗流程（如图7（a）所示），硅片表面涂覆光刻胶作为掩膜，进行第一次光刻，形成正面图形（如图7（b）所示）；在硅片表面溅射金属膜层，用于增强膜片反射率（如图7（c）所示）；剥离与光刻胶粘连的多余金属（如图7（d）所示）；二次光刻，硅片背面涂光刻胶，曝光形成圆腔图案（如图7（e）所示）；干法刻蚀未被光刻胶保护的硅片并达到所需的膜片厚度，在硅片背面形成深腔（如图7（f）所示）；去胶（如图7（g）所示）；最后，将敏感膜片与玻璃基座进行阳极键合（如图7（h）所示）。最终，所形成的硅敏感膜片厚度为40 μm，半径1.3 mm。利用划片机进行划片处理，分成单个的敏感单元，传感头外部形状为方形，中间带有直径1 mm的通孔，最终将单模光纤伸入尺寸相匹配的石英玻璃管，然后再将玻璃管插入到通孔中实现固接，确保腔体处于密封环境。

4 数据采集及解调方法设计

在解调系统的搭建过程中，利用光谱仪实现光谱接收，计算机实现数据处理。实际操作中，选用基于光纤法珀滤波器技术的MOI-sm125光纤光栅解调仪，该仪器具有内置大功率扫描激光源，包含了绝对波长参考，避免了外部波长校准的环节，提高了测量的精准性。同时，它还有很大的动态范围，在1 Hz的扫描速率下引起的噪声基底大约为60 dBm，共配置4个通道，其热稳定性及长期稳定性较好。该光纤光栅解调仪可扫描的光谱范围为1510 nm-1590 nm，采样间隔位5 pm，采样频率为2 Hz时，一个周期内大约采集16 000个点，每个点所包含的数据信息量之和高达30 k字，若仅凭人工筛选数据寻找有效值，会耗费很长的时间与精力，若直接对收集到的数据进行线性拟合或峰值检测等处理又会大大降低处理的速度及有效率，因而必须对采集数据进行恰当的处理，通过减小数据总量来保证信号提取的精度。在MOI-sm125智能光纤光栅解调仪中，虽然内置了峰值探测算法，但每个形状的中心波长具有至少3 dB～5 dB的对称反差。为了实现更通用且更准确的峰值探测，我们不采用内在的峰值探测算法，而是将智能光纤光栅解调仪中各通道的光谱数据自行提取出来，通过数据采集到计算机中进行后续编程处理。

本文在条纹计数法及多峰检测算法的基础上，提出了一种更为精确的数据处理方法，目的是在减少解调过程中光谱数据运算量的同时保证提取的数据可靠性，从而提高系统的有效性。该算法主要由滤波处理、极值判断和粗大误差剔除三部分构成，其具体流程如图8所示。

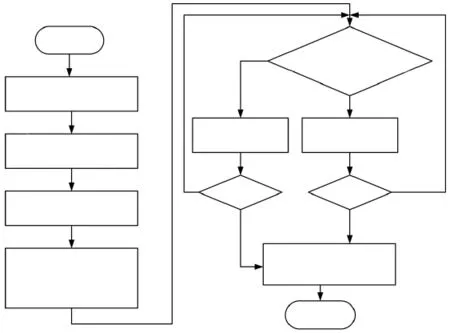
图8 数据处理流程图

在设计的算法中，首先对采集到的光谱数据进行提取，然后进行数据预处理即利用Smooth函数滤波，接着利用MATLAB自带函数Findpeaks对周期内的所有数据点进行局部极值点的寻找，利用公式计算出法珀腔腔长并根据格拉布斯准则剔除粗大误差，保证计算所得的全部腔长的有效性，最后对腔长求平均值，做出腔长变化与压力的关系曲线。

①滤波处理

通过对ENLIGHT软件保存的光谱数据进行二次绘图可发现，在光谱波形中存在许多毛刺，使得整体曲线存在较多的扰动，因此首先需要对光谱数据进行滤波处理，得到相对平滑的曲线以便于后期处理。调用MATLAB自带的Smooth函数，通过移动平均法对数据进行平滑处理。图9中蓝色部分为原始光谱信号，红色部分为滤波后光谱信号，可以看出经过滤波后的图形并没有产生偏移与失真，可以得到平滑的曲线，为后续的数据处理提供方便。

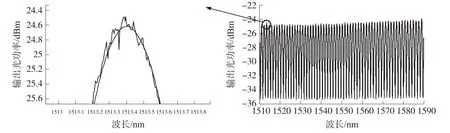
图9 滤波对比图

②极值判断

在之前的一些处理方法中，常常对采集到的光谱数据进行分组处理。一种方法是根据数据周期设置固定的分组，在单位数组内连续大于零的数值作为波峰数据，按坐标的大小顺序分别放入不同的数组中，然后逐个进行峰值检测；另外一种方法是先设定阈值，然后利用for语句循环实现动态窗口的分域，循环过程中每遇到连续的非零数据就存入数组中，完成峰值检测后，数组置零并滑向下一组数值，直至完成所有波峰的峰值检测［11］。尽管上述两种方法使用比较普遍，但第一种方法耗时较长，且当外界条件参数不同时采用固定点数进行分组会极大地降低求解精度，第二种方法虽然对于数据的分配更为合理，但在实际处理过程中容易将非波峰数据误判，需要后续的二次处理，使得整体处理的过程复杂化。基于上述经验，本次设计中直接进行局部极值点的寻找，调用MATLAB的Findpeaks函数，逐个查找向量中的波峰，即某一个元素比相邻两个元素的值都大，然后按照每列的搜索顺序标出波峰的值和相对应的横坐标位置。该方法不仅衔接紧密连贯，能够寻找到所有的光谱数据峰值，而且在光谱周期不完全相同时也能很好的运行，不会出现漏点误判的情况，具有良好的通用性。

③粗大误差剔除

当所有数据完成极值的提取，获得波长范围内产生干涉的所有波长之后，对相邻的波长进行计算得到法珀腔腔长。在传统的解调过程中，往往只选用双峰检测法，即选取相邻的两干涉条纹波峰的位置λ2和λ1，利用腔长公式（5）进行计算：

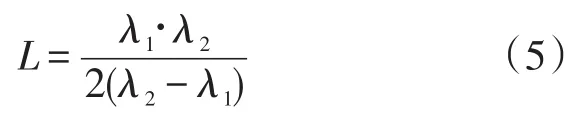
但是对于只采用两个主波峰（双峰法）计算出来的应变值，误差将直接加在两个波峰上，考虑到可充分利用所有的波峰信息，因此将传统的双峰算法改进为多峰算法，公式为：

式中，k为两干涉波长级次之差。通过算法改进，同等条件下应变的误差减小为原来的1/k，且随着应变的增加，波峰数的增多，改进算法对系统误差的抑制效果会更加明显。

但在实验过程中，由于外界扰动等因素，同一个波长范围内有时会出现两个距离非常近的极值点，如果利用该组数据进行计算会得到一个极大的腔长数值，造成整体数据的偏差。因此，需要对该错误结果进行数据剔除。在常用的几种判别标准中，格拉布斯准则对于数据的数量n要求不大，在判断的可靠性方面性能较优［12］。因此，本文选择格拉布斯准则为判别数据包含粗差准则。在判别过程中，首先选定危险率（异常数据出现误判的几率）α，若xn为可疑数据，则根据计算T值，其中，根据n及α，查表得到T0（n，α）值；如果T≥T0（n，α），则所怀疑的数据是异常数据，应予剔除。如果T＜T0（n，α），则所怀疑的数据不是异常数据，不能剔除。为使表达形式更加简单，可得出准则：当满足：，则判定该测得值含有粗差，应予以剔除。若某次判断所测数列值中有坏值，可剔除该值后重新计算xˉ，v，s等，在此依据判别准则判断剩余数值中是否含有坏值，直到全部剔除完为止。

从图10中粗大误差剔除前后的对比中不难看出，当某个腔长值相对偏值较大时，可以在数据剔除过程中将其去掉，避免其对整体计算的影响，使得最终计算结果更为准确。基于格拉布斯准则完成粗大误差数据剔除后，对保留下来的全部腔长值进行均值运算，得到平均腔长后作出法珀腔腔长随压力变化的关系曲线。

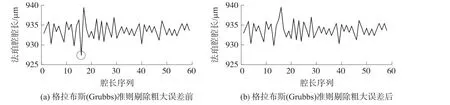
图10 粗大误差剔除对比图

5 系统测试

为了对解调方法的有效性进行客观的评判，设计了如图11所示的光纤压力传感相关测试及解调系统。该系统主要由光纤法珀压力传感元件，光纤光栅解调仪（MOI-sm125），计算机及温度/压力复合测试设备构成。实验测试时，将传感器放置在密封的真空压力室中，缓慢增压引起敏感膜片产生形变。与此同时，用光谱仪实时记录光纤FP传感器的输出光谱变化，利用计算机采集数据并根据所设计的解调方法计算出相应的应变值，得到法珀腔腔长与压力的变化关系曲线。

图11 测试系统装置图

在实际测试中，选取的压力范围为0～100 kPa，间隔为10 kPa，升压过程中光谱信息会存在一定的时间延迟及条纹波动，因此需要待压力稳定后，再开始记录解调系统输出的波长信息。当数据保存后，利用设计好的解调方法进行数据读取与运算，得到的测试曲线如图12所示。

图12 腔长-压力测试图

从图12可以观察到，随着外界施加压力值逐渐增加，光纤珐珀腔的腔长逐渐变短，即敏感硅膜片受到压力后沿轴向发生形变，在100 kPa的变化范围内，腔长变化约为6.23 μm，测试曲线线性度良好，在100 kPa的量程内其灵敏度可以达到62.3 nm/kPa。

传感头制作过程中，玻璃基座与硅片键合会使FP腔内封存一定量的空气，另外石英玻璃管本身也存在热膨胀效应，导致F-P传感器腔长随温度漂移。为检验该传感器的温度-压强交叉敏感性，在大气压下，将传感头放入烘箱中进行温度测试。实验表明，大气压下，腔长在20℃～130℃的范围内温度敏感系数为0.023 μm/℃，如图13所示。相应于温度-压强交叉敏感为0.37 kPa/℃，即10℃的温度变化导致压强的测量误差为满量程的3.7%。在室温和常压下，对传感头的静态腔长分辨率进行了测试，采用两倍的标准差作为传感器的压强测量分辨率，计算得到该压力传感器的腔长变化分辨率为8.05 nm，相应的所能测量最小压强变化为1.29 kPa。通过多次实验测量，可以得到其平均标准偏差σˉ=1.31 kPa，传感器的测量精度可表示为：

式中，YFS代表满量程100 kPa，可以计算出该传感器的精度可达3.93%。综合以上实验结果可知，所设计的解调方法能够较为准确的解调出光纤法珀压力传感器的输出信号。

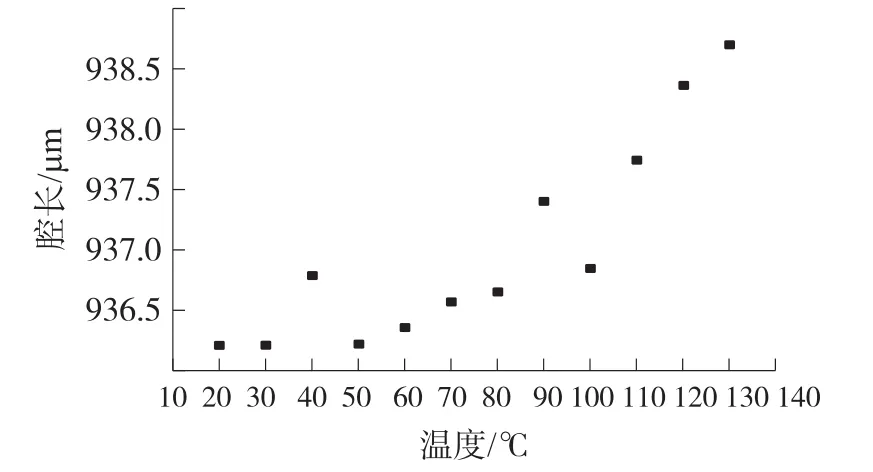
图13 温度敏感测量

6 结论

设计并制作了一种MEMS光纤法珀压力传感器，建立了敏感膜片挠度变化的理论模型，并实现了其二维和三维条件下的数值仿真。在相位解调方法的基础上，提出了能够应用于光纤传感系统的解调方法，搭建了测试系统并进行了相关实验，并对实验数据进行了处理。测试结果表明，在0～100 kPa的压力测量范围内，实验曲线的线性度良好，其灵敏度可以达到62.3 nm/kPa，温度敏感系数为0.023μm/℃。同时，该传感器结构简单且制作方便，测量分辨率可达1.29 kPa，证实了该MEMS光纤法珀压力传感系统具有一定的可行性，在后续的工作中将对传感器的性能做进一步的改善与提高。

［1］Ngajikin N H，Ling L Y，Ismail N I，et al.CMOS-MEMS Integration in Micro Fabry Perot Pressure Sensor Fabrication［J］.Jurnal Teknologi，2013，64（3）：83-87.

［2］Li M，Wang M，Li H.Optical MEMS Pressure Sensor Based on Fabry-Perot Interferometry［J］.Optics Express，2006，14（4）：1497-1504.

［3］Dai L，Wang M，Cai D，et al.Optical Fiber Fabry-Pérot Pressure Sensor Based on a Polymer Structure［J］.Photonics Technology Letters，IEEE，2013，25（24）：2505-2508.

［4］Yu Q，Zhou X.Pressure Sensor Based on the Fiber-Optic Extrinsic Fabry-Perot Interferometer［J］.Photonic Sensors，2011，1（1）：72-83.

［5］Lai C W，Yur J P，Liao C C，et al.Study on Optical Fiber Pressure Sensors with Temperature-Insensitivity Based on Fabry-Pérot Interferometry［J］.Recent Patents on Signal Processing，2011，1（1）：48-54.

［6］江小峰，林春，谢海鹤，等.MEMS FP干涉型压力传感器［J］.红外与激光工程，2014，43（7）：2257-2262.

［7］王代华，刘书信，袁刚，等.并联复用光纤法-珀加速度传感器及解调方法的研究［J］.光学学报，2010（6）：1776-1782.

［8］葛益娴，王鸣，闫海涛，等.基于相位解调的光纤MEMS压力传感器［J］.功能材料与器件学报，2008，14（2）：472-475.

［9］李学金，张百刚，姚建铨，等.一种光纤压力传感器的设计理论分析［J］.传感技术学报，2004，17（1）：133-135.

［10］陈绪兴，王鸣，戎华，等.基于波长解调的Fabry-Perot型光纤MEMS压力传感器的设计［J］.传感技术学报，2006，19（5）：1875-1877.

［11］张天地，贺锋涛，周强，等.光纤光栅解调系统的寻峰算法研究［J］.激光技术，2013，37（1）：36-39.

［12］张岩.运用格拉布斯准则原理确定公路定额测定中不合理数据［J］.科协论坛：下半月，2009（2）：99-100.

曹 群（1990-），女，吉林人，硕士研究生，主要研究方向为光纤压力传感，cxqnuc@ 126.com；

贾平岗（1982-），男，陕西人，博士，讲师，主要研究方向为光纤传感技术，高温压力传感技术，MEMS传感器技术研究，pgjia@nuc.edu.cn；

熊继军（1971-），男，湖北人，博士，教授，博士生导师，主要研究方向为传感器技术、微纳器件与系统研究，xiongjijun@nuc.edu.cn。

Design of MEMS Optical Fiber Pressure Sensor and Demodulation Method Implementation*

CAO Qun1，2，JIA Pinggang1，2*，XIONG Jijun1，2，ZHANG Hairui1，2，HONG Yingping1，2，FANG Guocheng1，2
（1.Science and Technology on Electronic Test&Measurement Laboratory，North University of China，Taiyuan 030051，China；2.Key Laboratory Instrumentation Science&Dynamic Measurement，Ministry of Education，North University of China，Taiyuan 030051，China）

A kind of MEMS optical fiber Fabry-Perot pressure sensor was proposed based on the pressure sensing principle which due to the change of cavity length caused by the deformation of sensitive diaphragm when pressure applied.The sensor’s theoretical model between sensitive diaphragm deflection variation with film thickness，radius and loading pressure was established.On the basis，the two-dimensional simulation using MATLAB and three-dimensional numerical simulation by Comsol Multiphysics software was performed and the processing fabrication of FP pressure sensing part was realized as well.Thus the demodulation method which can be applied to the optical fiber sensing was designed and related experiments were taken on after the implementation of optical fiber sensing pressure testing system.By employing the designed demodulation method，the sensor’s performance and characteristics can be tested and verified.The experimental results indicate that the linearity of sensor’s measured curve is good and broadly consistent with the results of numerical simulation，the sensitivity under 100 kPa is about 62.3 nm/kPa with a temperature sensitivity coefficient of 0.023 μm/℃，the measured resolution and precision are 1.29 kPa and 3.93%respectively that confirmed the method of MEMS optical fiber pressure sensing system performs a potential possibility.

optical fiber sensing；Fabry-Perot cavity；MEMS processing；demodulation method；MATLAB；Comsol Multiphysics

TP212

A

1004-1699（2015）08-1141-08

��2560；2575D；2575F；4190

10.3969/j.issn.1004-1699.2015.08.008

项目来源：国家杰出青年科学基金项目（51425505）；青年科学基金项目（51405454）

2015-05-14 修改日期：2015-06-23