基于Catmull-Rom插值算法光栅分辨率测试系统改进*

杨海马，王光斌，张 亮，苏仰庆，黄元申，张大伟，马贤淑

（1.上海理工大学光电信息与计算机工程学院，上海200093；2.中国科学院上海技术物理研究所，上海200083）

基于Catmull-Rom插值算法光栅分辨率测试系统改进*

杨海马1，2*，王光斌1，张 亮2，苏仰庆1，黄元申1，张大伟1，马贤淑1

（1.上海理工大学光电信息与计算机工程学院，上海200093；2.中国科学院上海技术物理研究所，上海200083）

为了减小探测器采集及软件处理导致的系统误差，提高光栅分辨率检测精度，利用半宽度法设计了一套满足李特洛条件的阶梯光栅分辨率检测系统。搭建了系统的光路，介绍了提高分辨率的方法，重点分析了探测器像元尺寸对系统分辨率测试精度的影响，提出了在LabVIEW软件中如何根据离散光谱信号并利用Catmull-Rom插值构造出连续光谱，提高半宽度法检测的精度。实验结果表明，在高分辨率测试系统中，通过软件算法对离散信号进行拟合分析，能有效的解决由像元尺寸造成的系统误差。

光栅；分辨率检测；插值算法；光谱曲线

光栅是光谱仪器的核心光学元件，分辨率是衡量光栅性能的重要指标，因此对光栅分辨率的测试结果将直接影响光栅光谱仪器的性能评价。目前对光栅分辨率的测试方法主要归纳为3类：①自然双线法，利用带宽较窄的自然谱线，经光栅衍射后在谱面上测量衍射光的分辨极限Δλ确定光栅的分辨率；②人工双线法，利用塞曼效应产生可调的单色谱线，利用谱面位置分析光栅分辨率极限；③谱线半宽度法，根据瑞利判据，用光电扫描或成像的方法测出谱线的半峰宽度Δλ，定量分析光栅的分辨率。谱线半宽度法因其简便、直观、有数据也有曲线图的特点成为最常用的测试方法。

目前，国内、外已经发表了许多关于光栅分辨率影响因素的文献，但对光栅光谱曲线中像元尺寸大小及提取算法中像元插值方法引起的分辨率影响分析的还不多。浙江大学的沈德洪最早提出了全面评价光栅分辨率的方法和装置［1-2］。中科院长春光机所的孔鹏、巴音贺希格等分析了设计参数如曲率、线槽周期误差等对光栅分辨率的影响，对于测试系统没有展开分析［3］。上海理工大学的裴梓任等分析了光栅分辨率中的窄缝、像元尺寸对分辨率的影响，但对光谱边界的提取方法的影响没有介绍［4］。中科院上海技物所的钱锋等研究了像元填充因子对谱线边界判断的影响，提出了加权质心算法确定中心谱线的方法［5］。

在利用半宽度法测量阶梯光栅分辨率的测试系统中，由光学系统造成的误差主要包括光学系统中照明系统、狭缝宽度、光学元件的像差等［6-7］。在实际测试时光谱图像的采集、分析是影响光栅分辨率计算的重要因素之一。受探测器像元尺寸大小的影响，采集到的原始图像一般为一系列离散的光谱点。在光栅分辨率较高的测试系统中，测得的原始谱线半高处的宽度（以下简称谱线半高宽度），其像的归一化物理尺寸可达100 μm。在一个半高宽度为100 μm，像元尺寸为15 μm×15 μm的CCD光栅分辨率测试系统中，谱线半高宽度所占的像元点数只有6.67个，造成实际计算的谱线半高宽具有较大的系统误差。为保障探测器的探测质量，探测器像元尺寸不可能无限小，常用的CCD探测器像元尺寸范围为3 μm～20 μm，因此不能通过减小像元尺寸的方法来提高光谱信号的采样点数量，只能通过软件计算的方法提高谱线半高宽度的计算精度。

基于以上分析，本文以阶梯光栅分辨率测试系统为例，分析了像元尺寸大小对谱线半高宽度计算的影响，设计了一套基于LabVIEW软件的分辨率测试系统，解决了在像元尺寸固定的情况下如何通过软件插值提高谱线半高宽度精度的方法，从而提高了传统光栅分辨率测试系统的极限测试精度和测试过程的自动化程度。

1 系统设计

1.1 系统装置

阶梯光栅是为利用高级次光谱获得高分辨率本领和大入射角而特殊设计的一种特殊光栅［8］。工作于Littrow条件下时，入射角等于衍射角等于闪耀角，光栅效率最高。阶梯光栅光谱分辨率检测系统的光路结构如图1所示。

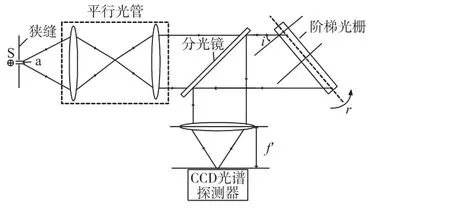
图1 系统光路结构

图1分辨率检测系统中阶梯光栅部分基本结构如图2所示。

图2 系统中阶梯光栅的基本结构

1.2 分辨率计算

在图1分辨率检测系统中，系统满足Littrow条件，即入射角i等于衍射角φ等于闪耀角θ时，光栅的衍射级次可以根据下式求得

阶梯光栅方程为：

式中：i为入射角，d为光栅常数，m为衍射级次，λ为入射波长，γ为光栅转角，φ为光栅衍射角。

光栅线色散率倒数为：

式中：f′为焦距。

进而求得系统的分辨极限为：

式中：n为光谱曲线半高宽度所占像素点，p为感光元件像元尺寸。

由于检测系统狭缝具有一定宽度，相当于扩展光源，经过系统成像后也包含在系统的分辨极限之内，为减小狭缝宽度和像差对系统分辨率造成的影响［9-10］，对（4）式进行修正，得到光栅分辨极限

式中：a′狭缝宽度在光栅检测中带入的光谱展宽，设a为狭缝宽度，应用色散公式计算得δ′为像差［11］。

利用公式计算出的光栅分辨率可表示为：

2 采集系统算法改进

实际检测系统中根据离散点计算谱线的半高宽度所占像元个数n时存在一定的随机误差，对系统分辨极限计算造成很大影响。为保障谱线半高宽度计算精确度，需利用软件算法对离散信号进行平滑拟合，修正谱线半高宽度计算公式。

2.1 探测器感光像元对分辨率精度测试影响

测试系统试验选用ALLIED公司Prosilica GT系列中的GT4907和GT1290面阵CCD作为探测器，对应的像元大小分别为3.75 μm×3.75 μm、7.4 μm×7.4 μm。

①选用像元尺寸p为7.4 μm的GT4907采集的离散光谱信号，如图3所示。

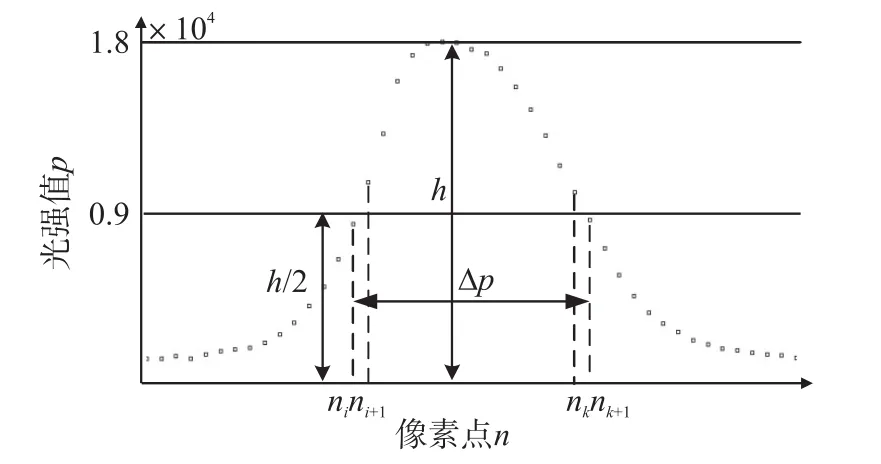
图3 像元为7.4 μm对应离散光谱点

由半宽度法计算光栅分辨率时，需求出光谱曲线波峰上边缘和波峰下边缘光强值等于波峰值一半所对应的两个点的横坐标nl、nr，得到谱线半高宽度所占像素点的个数n，如式（7）所示。

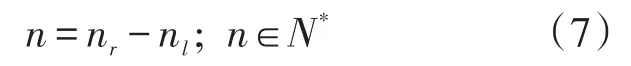
由于采集的光谱信号为离散信号，实际采样点中不一定存在光强为波峰值一半的点，只能寻找光强值离波峰值一半最近的两个点近似替代nl、nr，在图3中近似点为ni、nk+1。

根据像元尺寸求出谱线半高宽度Δp，如式（8）所示。

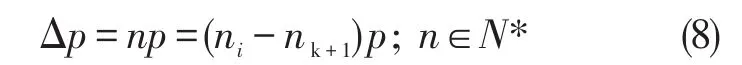
由于ni、nk+1为nl、nr近似值，所求的半宽度Δp存在一定随机误差。在同一次实验中，选用像元尺寸为3.75 μm的GT1290采集的离散光谱信号，如图4所示。

图4 像元为3.75 μm对应离散光谱点

根据图3、图4可知，最小谱线半高宽度Δpmin= (nk-ni+1)p，最大谱线半高宽度Δpmax=(nk+1-ni)p，实际计算得到的谱线半高宽度Δpl∈[Δpmin,Δpmax]。为减小实际测得值的随机误差，需减小区间范围[Δpmin,Δpmax]，（Δpmax-Δpmin）的计算如式（9）所示。

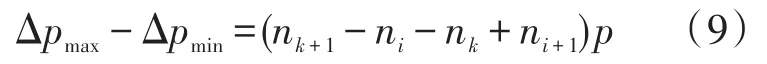
对式（9）进一步简化得到：

通过式（10）可知，减小像元尺寸可以缩小由于像元点离散造成的随机误差的范围，提高谱线实际半高宽度的计算准确度。

2.2 Catmull-Rom插值算法提高系统精度

CCD对于图像的采样过程，实际上就是对于光谱线轮廓强度的一个采样过程。利用CCD作为探测器时，像元大小很重要，而CCD探测器受到量子效率、响应度、噪声等效功率和探测深度的影响［12］［13］，为保证CCD的性能像元大小受到很大限制，因此在探测器像元尺寸固定的情况下需要通过计算机软件算法提高光谱半高宽度的计算精度。

2.2.1 Catmull-Rom插值算法简介

Catmull-Rom样条函数［14］利用目标节点前后2个节点的值计算出样条函数在该节点处的导数，并通过相邻4个节点的坐标构造出经过中间2点的曲线。Catmull-Rom曲线每个分段拥有四个控制点，假如将这四个顶点分别命名为 Pi-2、Pi-1、Pi、Pi+1，则可以在Pi-1Pi之间构造出一段连续平滑的曲线，通过拼接构造的每一段样条曲线便可以构造出一条完整的连续曲线。Catmull-Rom分段计算的曲线结果如图5所示。

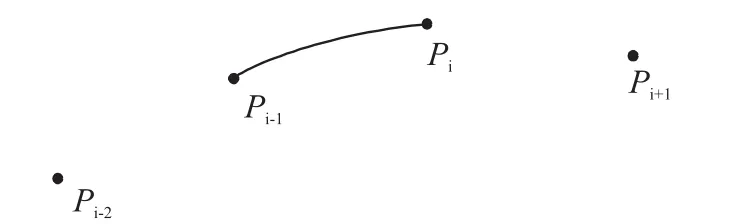
图5 Catmull曲线计算示意图

该曲线函数为一条3次曲线，可用式（11）表示。

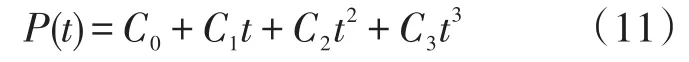
式中：浮点坐标t∈[0,1]，样条函数系数C0～C3由P(t)在端点t=0、t=1处的约束条件求得，如式（12）所示。

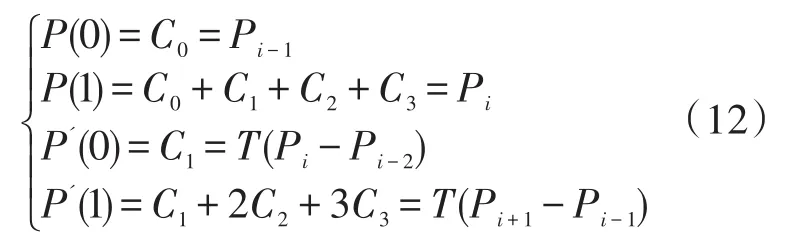
式中T称为形状因子，由式（12）求得系数C0～C3后带入式（1），得到曲线方程P(t)如式（13）所示。

式中M为样条曲线差值矩阵，如式（14）所示。

当样条用于离散点连续平滑时，T取0.5为最佳值［15］，根据式（13）和式（14）可求得插值点Pi-1Pi之间的Catmull连续曲线。

2.2.2 连续Catmull光谱曲线

为解决谱线离散光谱信号对半高宽度计算的影响，本文将Catmull算法应用于离散光谱信号的连续平滑，拟合光谱曲线，减小系统随机误差。

将图3所采集的离散光谱信号点从左至右依次编号为n1，n2，……，nq。

①首先，根据“首段曲线补齐”的方法，设定n1，n2，n3，n4为4个控制点，计算n1n2段曲线。

②设 ni，ni+1，ni+2，ni+3为控制点，依次计算ni+1ni+2之间的曲线，i=1，2，…。如图6所示。

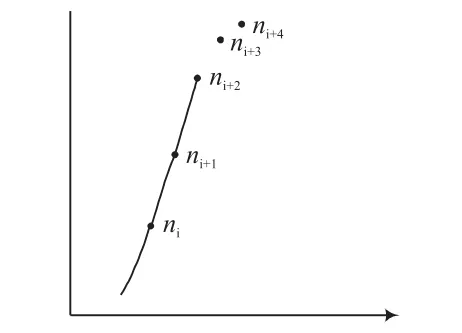
图6 连续Catmull光谱曲线计算

③设置末端控制点为nq-1nq，nq-1，nq，nq，计算nq-1nq段曲线。

据上述方法构建连续Catmull光谱曲线，结果如图7所示。

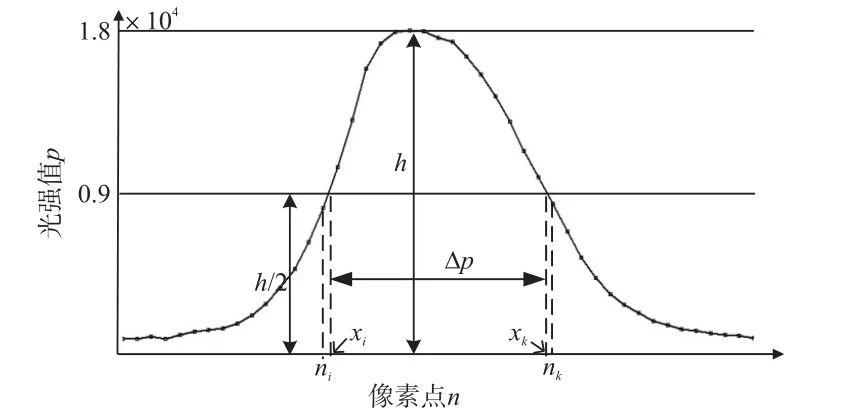
图7 完整Catmull光谱曲线

由于计算机只能处理离散点，在利用PC机软件构造Catmull光谱曲线时将每段t值分为若干段，利用LabVIEW软件搜索光强值为h 2的点并返回对应的横坐标xi和xk，如图7所示。

并对式（7）进行修正得到方程如式（15）所示。

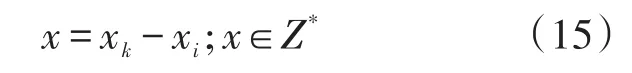
谱线半高宽度Δp，如式（16）所示。

式中：x为谱线半高宽度对应的像素点，x不再为自然数，而是一个正实数，如式（8）相比，Δp的计算更为精确。

3 实验结果与分析

本文阶梯光栅分辨率检测系统参数为：

狭缝宽度：a=50 μm，入射角：i=63°，光栅转角：γ=6.9°，光栅常数：d=18 986.14nm。实验中采用低压汞灯气体放电光源，探测器型号为GT4907。

利用离散光谱信号点直接测得的谱线半高宽度所占像素点为n，利用Catmull-Rom插值算法拟合改进后计算得到的谱线半高宽度所占像素点为x，在不同输入波长λ（单位：nm）下测得的n、x值如表1所示。

表1 谱线半高宽度对比

表1中由Catmull连续光谱信号曲线所计算的像素点宽度与直接根据离散光谱信号计算的像素点宽度之差的绝对值最大值为0.39个像素点，

记光栅理论分辨本领为R，利用离散光谱信号点直接测得光栅分辨本领为Rl，利用Catmull-Rom插值算法拟合改进后计算得到光栅分辨本领为Rc，在表1不同输入波长λ（单位：nm）下，测得结果如表2所示。

表2 分辨本领对比分析

表2中对应波长下，直接由离散光谱信号曲线测得的光栅分辨本领、利用Catmull-Rom插值算法拟合改进后计算得到光栅分辨本领与理论光栅分辨本领之差绝对值曲线如图8所示。

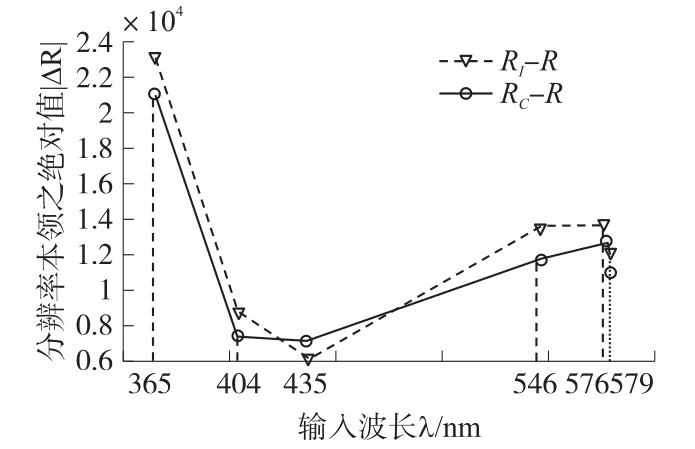
图8 分辨本领之差绝对值曲线

图8可以看出：利用Catmull-Rom插值算法拟合改进后，整体上比波动要小，即整体上Rc比Rl更接近于R。

直接根据离散光谱信号计算的像素点n存在较大的随机误差，可能大于实际光谱半宽高度所占的像素也可能小于实际光谱半宽高度所占的像素。由拟合改进后的Catmull-Rom光谱信号曲线计算的像素x虽更接近于实际光谱半宽高度所占的像素，但并不一定小于n（如表1中输入波长为435 nm时x小于n）。根据式（4），在相同的测试系统和输入波长下，试验测得的谱线半高宽度所占像素n越大，计算得出的系统分辨极限越大，测得的光栅分辨本领越高。目前的光栅分辨率测试系统中实际测得的光栅分辨率很难达到光栅的理论分辨率。即便实际测试时直接由离散光谱点计算得到的像素点n小于实际光谱曲线半高宽度像素，造成计算得到的光栅分辨率本领偏大，也没有超过光栅理论分辨率，反而表现为计算得到的分辨率Rl更接近理论分辨率R。因此会出现利用离散光谱点计算的分辨率更接近于光栅理论分辨率的情况。总体上利用Catmull-Rom插值算法改进后检测得到的光栅实际分辨率更接近于光栅的理论分辨率，计算结果更为准确，能够更真实的反映光栅的实际分辨本领。

4 总结

文章介绍了利用半宽度法检测阶梯光栅分辨率的系统结构及计算方法，分析得到在较高的光栅分辨率检测系统中，采集系统的误差主要由探测器性能参数造成。在保证探测器性能的前提下，应尽可能选用像元尺寸参数小的探测器。对采集的离散光谱信号利用Catmull-Rom插值算法构造Catmull光谱曲线对半宽度求解公式进行修正，能有效的解决离散光谱点造成的随机误差，减小像元尺寸对光栅分辨率检测造成的影响，提高光栅分辨率检测系统的测试精度。

［1］沈德洪.光栅分辨率测试装置的设计［J］.浙江大学学报，1985，6（19）：137-142.

［2］Engman S，Lindblom P.Multiechelle Grating Mountings with High Specral Resolution and Dispersion［J］.Appl Opt，1982，21：4363-4367.

［3］孔鹏，巴音贺希格，李文昊，等.曲率半径误差对平场全息凹面光栅分辨率的影响及其补偿方法［J］.光谱学与光谱分析，2011，31（5）：1435-1439.

［4］裴梓任，黄元申，张大伟，等.Offner型成像光谱仪波长使用范围和光谱分辨率研究［J］.光子学报，2014，43（7）：0730004-1.

［5］钱锋，贾建军，张亮，等.捕获、跟踪、瞄准系统中光斑探测相机的定位精度［J］.中国激光，40（2）：0205007-1

［6］杨晓冬，李正灯，李惠玲，等.光栅光谱仪入射与出射狭缝宽度对测量谱线线宽影响研究［J］.嘉应学院学报：自然科学，2008，26（6）：38-41.

［7］丁卫涛，黄元申，张大伟，等.中阶梯光栅刻划误差要求分析［J］.光电工程，2013，40（9）：68-75.

［8］武旭华，朱永田，王磊.高分辨率阶梯光栅光谱仪的光学设计［J］.光学精密工程，2003，11（5）：442-447.

［9］Churin E G，Bayvel P，Stavdas A，et al.Optimization of Rowland Circle Mounts for Grating Demultiplexers and Narrow-Band Spectrographs［J］.Opt Lett，1996，21（14）：1084-1086.

［10］侯立群，赵雪峰，冷志鹏，等.光纤光栅应变传感器温度补偿计算值的改进［J］.传感技术学报，2014，27（1）：70-73.

［11］唐玉国，宋楠，巴音贺希格，等.中阶梯光栅光谱仪的光学设计［J］.光学精密工程，2010，18（9）：1989-1995.

［12］潘明忠，刘玉娟，陈少杰，等.中阶梯光栅光谱仪CCD相机的设计［J］.光学精密工程，2012，20（8）：1725-1731.

［13］汪家奇，唐祯安.与CMOS工艺兼容的皮拉尼传感器研究［J］.传感技术学报，2013.26（1）：31-33.

［14］陈红倩，李凤霞，张庆义，等.一种渐进式平滑轨迹线标绘方法［J］.系统仿真学报，2012，24（2）：357-360.

［15］魏美荣，蒋林.一种自适应Catmull-Rom样条图像缩放算法的设计实现［J］.微电子学与计算机，2011，28（12）：63-68.

杨海马（1979-），男，上海，博士，长期从事光电智能仪器设计及电气控制方面的教学与科研工作，主要研究方向为光电智能仪器，ATP跟瞄技术，信号和信息处理等，snowyhm@sina.com；

王光斌（1990-），男，重庆，硕士研究生，主要从事光电仪器设计及光栅特性检测方面的研究，132350265@st.usst.edu.cn。

The Improvement of Grating Resolution Testting System Based on Catmull-Rom Interpolation Algorithm*

YANG Haima1，2*，WANG Guangbin1，ZHANG Liang2，SU Yangqing1，HUANG Yuanshen1，ZHANG Dawei1，MA Xianshu1
（1.School of Optical-Electrical and Computer Engineering，University of Shanghai for Science and Technology，Shanghai 200093，China；2.Shanghai Institute of Technical Physics of The Chinese Academy of Sciences，Shanghai 200083，China）

In order to reduce the system error caused by detector acquiring and software processing，and improve the accuracy of echelon grating resolution，a resolution detection system which satisfied Littrow condition was designed by using the half wave width method.The optical structure of the detection system was built and the improved detection method was introduced.Then the grating resolution influenced by detector pixel size was analyzed.By using Catmull-Rom interpolation algorithm to fit a continuous spectral curve，the accuracy of half wave width according to the discrete spectrum was improved in LabVIEW.The experimental result also showed that the system error caused by pixel size can be effectively reduced by fitting analysis of discrete signal in the high resolution testing system.

gratings；resolution measurement；interpolation algorithm；spectral curve

O433.1

A

1004-1699（2015）08-1136-05

��7220；7230E

10.3969/j.issn.1004-1699.2015.08.007

项目来源：国家自然科学基金青年基金项目（61302181）；上海市教委科研创新项目（13YZ111）；上海市自然科学基金项目（14ZR1418400）

2015-01-16 修改日期：2015-05-31