基于差分曲率的自适应反锐化增强算法

贺梦颖

(中北大学 信息与通信工程学院，山西 太原 030051)

反锐化掩膜技术(Unsharp Masking technique，UM)［1～3］是一种常用的图像增强技术，传统的反锐化增强采用不同的滤波方法提取图像的高频细节成分，然后将抽取出来的高频成分缩放一定倍数后与原始图像进行叠加得到增强后的图像。然而这样得到的结果在灰度变化剧烈的边缘区域会产生过增强现象，而且容易在噪声可见度较大的平滑区域放大噪声［4］。

为了解决这些问题，更好地利用反锐化掩膜进行图像增强。G.Ramponi 提出了立方反锐化掩模技术，一种非线性反锐化算法［5］，利用局部梯度的平方对细节部分进行缩放，但仅能增强高亮度区域的图像细节，并相对减小噪声敏感度。Kwok［6］提出了一种基于像素强度的自适应增益反锐化掩膜算法，然而这种算法往往会放大图像的背景噪声。这样得到的增强图像虽然在减小噪声和克服光圈效应方面性能优越，但是对于细节部分的增强处理仍旧不尽人意。

为了更好地解决上面所说的问题，提出了新的基于差分曲率自适应反锐化掩膜算法。新算法利用图像的局部差分曲率来分辨图像的细节和噪声区域，并自适应地分别以不同的增强因子控制这两个区域的增强程度并尽量减小噪声的干扰。同时考虑到人眼视觉的部分特性，一方面对低灰度和高灰度区进行大幅度地增强，另一方面小幅度增强人眼不太敏感的中间灰度区，以便获得比原图像视觉质量更好的增强图像。

1 本文提出的自适应反锐化掩膜算法

为了克服前面提到的一些经典反锐化掩膜算法中存在的过增强或者弱增强的缺点，文章对增强因子进行了深入研究并利用图像的局部信息进行了一些改进。图1 的原理方框图给出了新算法的主要步骤和改进之处。

图1 新算法的基本原理框图

具体计算如下面给出的等式(1)所示:

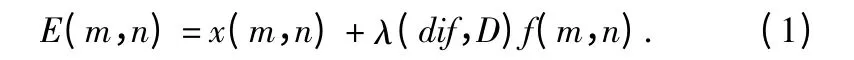
x(m，n)是输入图像，E(m，n)是最终的锐化增强结果，f(m，n)是经过高通滤波后的结果，λ(dif，D)则是用来控制锐化程度的增强因子。新算法主要是利用原始图像的邻域差分曲率［7］和图像像素与图像中值的差来区分图像中不同的区域，然后针对其特点进行不同程度的增强。

1.1 邻域差分曲率

文章在增强因子的研究上所做的工作之一就是将图像像素值周围邻域差分曲率值D 的大小与边缘、细节区域的关系考虑进去。分析结果表明:图像梯度值小的区域可能是平坦区域或者弱边缘区域，而梯度大的区域有可能是边缘区域也有可能是噪声区域。为了进一步更好地区分出图像中的边缘区域与平缓区域，我们引进了差分曲率这个指标。

有研究表明二阶导数能够有效地区分一维信号的边缘和斜坡。将其推广到二维数字图像中后，出现了一种新的利用图像二阶导数来区分边缘点和平缓区像素点的指示因子，其表达式如下所示:

其中，D 表示能够区分边缘像素点和平缓区域像素点的差分曲率值。uηη和uξξ分别表示图像中沿着梯度方向和垂直于梯度方向的二阶导数，而|·|则表示绝对值的操作运算。这里uηη和uξξ的表示如下:

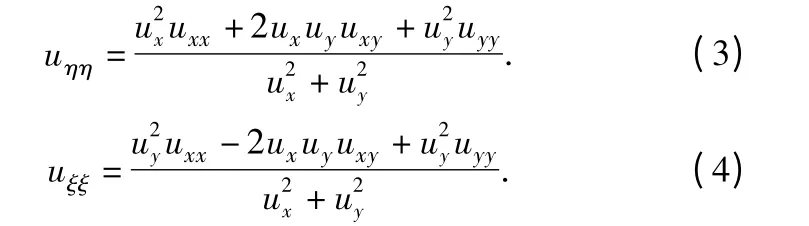
这里，式(3)和(4)中的ux，uy是图像在x 和y 方向的一阶导数，用来表示图像在x 和y 方向上的梯度变化。uxy，uxx，uyy则是图像的二阶导数，它们表示的是图像梯度的变化量。

下面，对新的指示因子差分曲率D 的取值情况进行了分析，同时也给出了如何利用差分曲率D 来区分图像的边缘点和平缓区像素点的方法:

1)对于处在图像中的边缘区域的像素点而言，此区域中图像的梯度和梯度变化都较大，按等式(3)计算出的|uηη|值较大。而按等式(4)计算得到的值则比较小，这样它们之间的差值即差分曲率D 也就比较大。

2)对于平坦区域和斜坡区域来说，区域的梯度和梯度变化量都较小，这样得到的也都会比较小，它们之间的差值D 也就较小。

本文中采用的是中心差分，x 和y 方向的一阶中心差分如下所示:

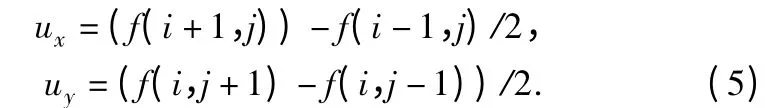
对于图像矩阵像素点f(i，j)而言，利用差分方程对x 方向上的二阶导数进行推导后表示如下:

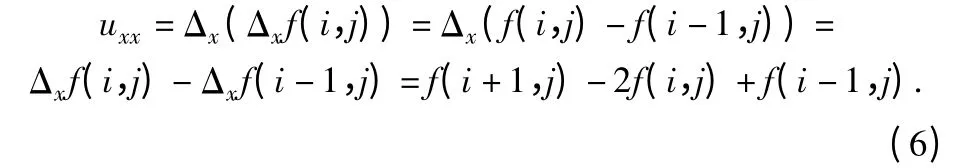
同理可得y 方向上的二阶导数公式:

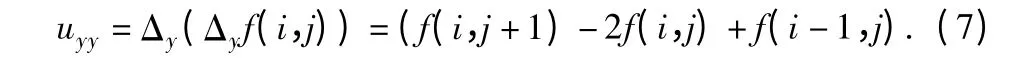
进而可推出在x 和y 方向上的偏导数uxy:

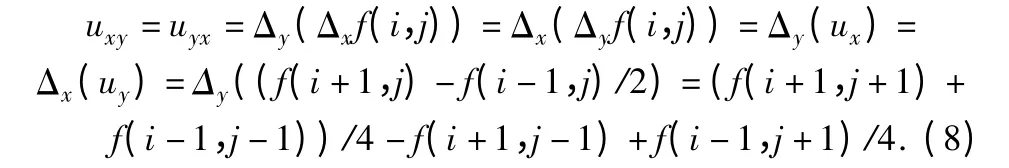
1.2 人眼视觉特性

新算法在利用图像邻域差分曲率的基础上还结合了HVS 人类视觉系统的部分特点。HVS 利用人眼视觉对中间灰度区域灰度变化比起低灰度和高灰度而言更加敏感的特性，正如等式(9)所表示的那样:

这里的dif 表示图像像素x 与图像中值middle 之间的差值。dif 越大，当前像素点归于高灰度或者低灰度区域，在邻域差分曲率固定时，针对这个像素的增强程度较大。反之，dif 越小，此时针对这个像素的增强程度也就较小。

1.3 算法的实现

经过上面的分析，影响增强因子的因素有两个:它们分别是图像邻域的差分曲率值D 以及当前像素与图像中值的差值dif 如图1 中所表示的λ(dif，D)。本文利用自然指数函数的单调递增特性，将增强因子表示成如下列式子所示:

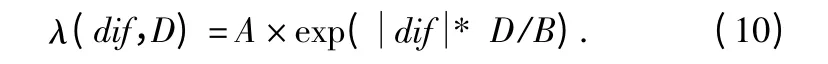
这里的A 和B 都是常数，可通过人为地根据实际应用来设定。根据经验和我们多次实验的结果将这两个参数设为A∈(0，1)，B∈(1 000，10 000)。

2 实验结果与讨论

这里使用了一幅尺寸大小为256 ×256 的lena 图像来进行仿真验证本文提出的新的锐化增强算法的性能。如图2所示作为原始图像，使用新算法和其他增强算法包括G.Ramponi 提出的立方反锐化掩膜增强算法，文献［6］中的调整增益的自适应反锐化掩膜增强算法对其进行处理来验证算法的有效性。

图2 Lena 图像经不同算法增强后的结果图像对比

如图2 所示，从图像(b)可以看出:图像中的细节锐化效果不太明显，丢失了帽檐和流苏部位的部分细节，虽然噪声较小，但是没有达到锐化的基本要求和目的;而从图像(c)中可以分析得到:图中的细节部分的锐化程度比较明显，但与此同时结果图像的噪声干扰也非常突出，使得图像的脸部和帽子流苏部分的细节与边缘被噪声干扰不易辨别。与图像(b)比较:本文提出的算法能较好地抑制过锐化效果，更好地区分噪声和边缘区，信噪比更高。与图像(c)比较新算法有更好的锐化效果，对于细节部分的强调更加明显，使得结果图像的视觉效果更佳。

除了主观的评价外，图像的客观评价方法对于增强算法的应用与改进也起着很大的作用［8］。因此本文还利用了四种客观评价参数包括图像信息熵［9］H(p)、峰值信噪比PSNR、图像细节－背景方差比DV/BV［10］来对图像进行分析和比较。

表1 列出了对图4 中来自不同增强算法处理之后的结果图像的客观质量评价。从表中可以看出，新算法对比其他几种增强算法而言，其信息熵、峰值信噪比、细节－背景方差都是最佳的，这说明新算法在图像的细节增强和边缘锐化以及抑制噪声方面从客观评价的角度来说有较好的表现。同时考虑到这几种算法都是针对图像全局像素进行计算，再观察表1 中给出的程序的运行耗费时间，可以得出:改进算法的计算比较简单，耗时更少。

表1 Lena 图像质量评价参数

3 结论

文章提出了一种基于图像差分曲率的自适应反锐化掩膜增强算法，它采用局部曲率差利用二阶导数区别斜坡和边缘的性质，能很好地分辨图像中的细节、边缘和平缓区域，同时利用人眼视觉特性对图像增强因子进行改进以便实现图像不同区域的自适应增强。改进后的算法克服了传统反锐化掩膜对图像进行整体增强和容易放大噪声的缺点。实验结果证明，该算法既能有效地增强图像边缘细节，还能有效地抑制噪声。

［1］苏晓芸.基于小波理论的医学图像增强研究［D］.哈尔滨:哈尔滨工业大学，2011.

［2］王婷，上官宏，刘袆，等.基于顶帽变换的反锐化掩膜算法［J］.计算机工程与设计，2014(1):198－202.

［3］刘艳莉，桂志国，张权，等.基于局部梯度和复杂度的反锐化掩膜法［J］.仪器仪表学报，2014(7):1539－1545.

［4］徐艳丽，谭剑.基于非线性反锐化掩膜的DR 图像边缘增强［J］.中国医学物理学杂志，2010(4):2013－2015.

［5］Panetta K，Zhou Y，Agaian S，et al.Nonlinear Unsharp Masking for Mammogram Enhancement［J］.IEEE Transactions on Information Technology in Biomedicine，2011，15(6):918－928.

［6］Kwok N M，Shi H Y，Fang G，et al.Intensity-based Gain Adaptive Unsharp Masking for Image Contrast Enhancement［C］.Image and Signal Processing (CISP)，2012 5th International Congress on.IEEE，2012:529－533.

［7］Chen Q，Montesinos P，Sun Q S，et al.Adaptive Total Variation Denoising Based on Difference Curvature［J］.Image and Vision Computing，2010，28(3):298－306.

［8］周景超，戴汝为，肖柏华.图像质量评价综述［J］.计算机科学，2008，35(7):1－8.

［9］Liu Y W，Li J W.Image Enhancement Based on Fractional Differential and Image Entropy［J］.Advanced Materials Research，2010:232－235.

［10］张聪.工业射线图像锐化增强算法研究［D］.太原:中北大学，2011.