基于半波激励的磁调制传感器设计与验证

王隆伟，王 鲜，冯则坤

（华中科技大学光学与电子信息学院，武汉430074）

基于半波激励的磁调制传感器设计与验证

王隆伟，王 鲜*，冯则坤

（华中科技大学光学与电子信息学院，武汉430074）

基于磁调制传感器的工作原理，创新性的提出了通过采用半波激励信号简化设计双磁芯磁调制传感器的方法。传统磁调制传感器是在环形磁芯一次绕组中通以完整的方波、正弦波或锯齿波作为激励信号，然后提取磁芯二次绕组中感应信号的二次谐波来对被测直流信号进行检测的，此二次谐波反映被测直流信号的大小与方向。笔者通过实验发现，若通以半波激励，可反映被测直流信号的谐波由二次谐波变为一次谐波，此时相敏检波电路参考信号无需倍频，因而在器件中可省去倍频电路。分别采用方波、正弦波和锯齿波及其相应的半波作为激励信号进行了实验分析，结果表明，半波激励可以获得更为理想的检测波形，能更好地反映被测电流的大小，提高传感器的灵敏度。

磁调制；二次谐波；一次谐波；半波激励

在电子电力设备中，时常需要对漏电流等微弱直流电流（多为mA级）进行检测，其检测方法主要包括小电阻取样、霍尔电流检测法以及磁调制法等［1］。其中电阻取样方法需要将采样电阻接入电路回路中，对原有电路会产生一定的干扰；霍尔电流检测法利用霍尔效应实现直流电流检测，但其受温度变化影响大，产生干扰大，测量弱电流灵敏度比较低［2］；磁调制电流检测法具有检测的弱电流范围宽、灵敏度高、高线性度等优点，具有良好的应用前景。传统磁调制传感器多使用倍频磁调制方法，此方法是提取传感器磁芯探头中检测端信号的二次谐波对被测直流信号进行检测，此二次谐波可以反映被测直流信号的大小以及方向，对此二次谐波进行直流整流，然后输出直流信号。此方法之所以称之为倍频磁调制法，是由于在对二次谐波进行整流鉴相的过程中，需要一个参考信号，此参考信号通常情况下由激励源信号通过一个倍频电路产生，以达到整流和鉴相的目的，因此称为倍频磁调制法。但使用此方法的磁调制直流传感器的信号处理电路相对复杂，其主要信号处理电路包括：信号放大电路、带通滤波器、倍频电路、相敏检波器以及低通滤波器等。同时传感器的信号干扰比较大，因而有必要对磁调制传感器的信号处理电路进行优化设计，以进一步改善其应用特性［3-16］。

本文针对磁调制直流电流传感器的原理进行数学分析，创新性的提出并实验验证了一种电路简化设计方法。即通过改变激励源信号使检测信号由二次谐波转变为一次谐波，而方法是简单的改变激励源信号，将以往使用的激励源信号如：方波、正弦波、锯齿波等激励源信号，由完整的波形变为半方波、半正弦波、半锯齿波波形，将这些信号波作为激励信号驱动磁调制传感器，可以达到使检测信号由二次谐波转变为一次谐波，因此在信号处理电路中可以省去倍频电路，简化器件的信号处理电路，同时可消除倍频电路对器件和激励信号源的干扰，提高了器件的灵敏度。

1 典型磁调制传感器的工作原理分析

图1为传统磁调制传感器的工作原理图。在一个环形磁芯（一般采用高磁导率、高矩形比和低矫顽力的铁镍合金磁芯）上分别绕有一、二次绕组，其中一次绕组W1为激励绕组，绕线N1匝；二次绕组W2为检测绕组，绕线N2匝。磁环的截面积为S，磁导率为μ，内外径分别为r1和r2，磁环的截面边长为a（实验中使用磁环的截面为正方形），I1为穿过磁芯中心的被测电流。

图1 磁调制传感器的工作原理

在一次绕组W1中通以交变激励方波电流信号I2，当被测电流I1为0时，检测绕组中输出信号只含有奇次谐波；而当被测电流I1≠0时，根据周期函数的傅立叶级数变换，对方波进行傅立叶变换得到：

式中：A为激励方波的振幅，ω为角频率，T为周期。

则产生磁场强度He可表示为：

H1为被测电流I1在磁芯中产生的磁场强度，当激励电流从0开始增加时，磁芯工作在线性区，即图2中-Hs＜H＜Hs时，可以认为磁芯的磁导率μ是常数，如图2所示。

图2 磁导率随磁场的变化曲线

图3可以看出，方波激励下对应的磁导率波形，磁导率的函数为周期为T/2的偶函数，其频率为2ω。对其进行傅立叶变换得到：

u1为直流分量。

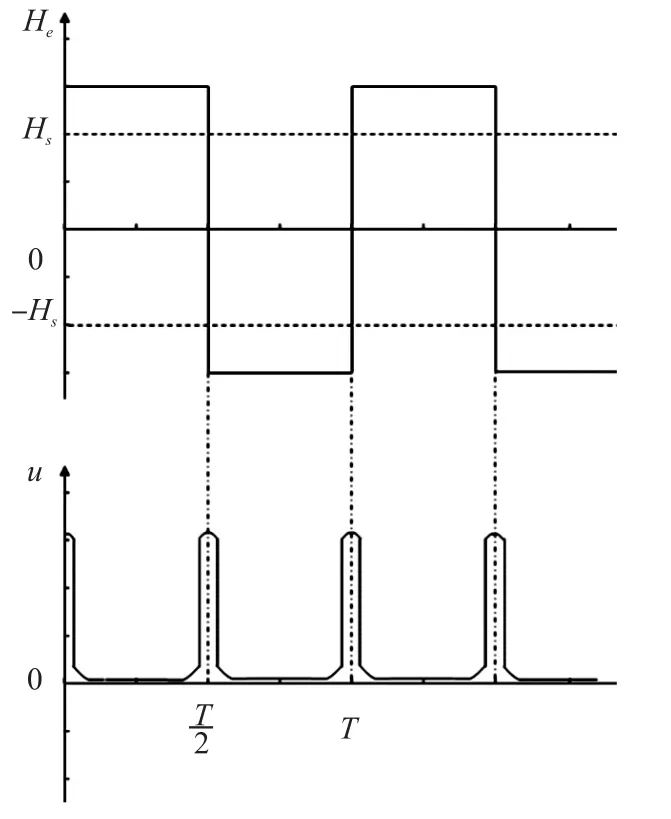
图3 方波激励下对应的磁导率波形

由式（2）和式（3）可得到检测绕组W2的感应电压：

2 半方波激励下的磁调制传感器的数学分析

实际应用中，对（5）式中的二次谐波进行提取，其频率为激励频率的两倍，注意到提取二次谐波后需要进行相敏检波，而相敏检波的参考信号必须与被检测信号频率同频，因此需要建立一个二倍频电路来产生二倍频率参考信号；该倍频电路不但会增加传感器整体的功耗，并且会对检测信号产生一定的干扰。笔者通过实验发现，改变激励信号的波形可有效简化这一部分电路，方法是将激励方波信号通过一个二极管，使激励信号变为半方波信号（如图4所示），可将二次绕组端需要提取的检测信号由二次谐波变为一次谐波，省去了倍频电路。

图4 半方波激励信号的波形

对图4所示的激励波形进行傅立叶变换：

则磁芯的磁场强度为：

再由图4分析磁芯的磁导率变化波形，磁导率在半波激励下的波形如图5所示。此时的磁导率波形的角频率为ω，周期为T，与激励信号同频。对其进行傅立叶变换：

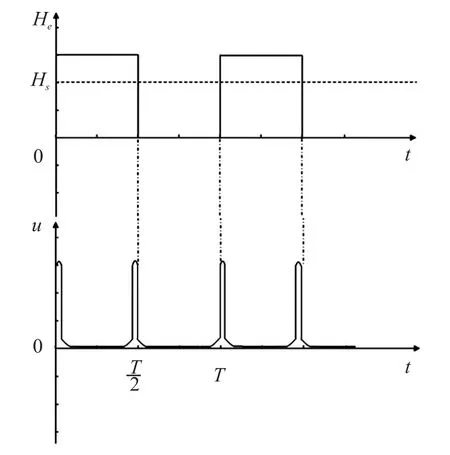
图5 半方波激励下的磁导率波形

在实际应用中，磁调制传感器通常使用双磁芯差动结构，如图6所示。在此结构下，式（13）的第一项将被双环抵消掉，第二项的大小变为2倍，提取第二项的一次谐波即可得到可以反映被测电流大小和方向的信号。因而，采用半方波激励可以简化磁调制传感器的结构，且对原有电路的其他部分不需要进行大的改动。

图6 实际应用的双磁芯差动结构磁调制传感器工作原理

3 实验验证

基于上述数学计算分析，采用图6所示的双磁芯差动结构磁调制传感器进行实验验证。在激励端分别通入方波（图7（a））与滤去方波正边的半方波（图7（c）），再将检测绕组感应电压通入相应的带通滤波器后使用示波器分别观察其波形。实验中使用的激励频率都为10.00 kHz，幅值为6.5 V，通入的电流为3.8 mA，得到实验结果如图7所示。在方波激励下（图7（a）），得到的检测绕组20 kHz滤波后的波形（图7（b））频率为20 kHz，幅值为85 mV（最大点）；在半方波激励下（图7（c）），得到的检测绕组10 kHz滤波后的波形如图7（d）所示，其频率为10.00 kHz，幅值为160 mV（最大点）。比较图7（b）与图7（d）的波形可以看出，方波激励下检测波形（图7（b））并不规则，主要原因在于实际方波激励无法达到真正的理想方波波形，存在一定的不对称，其占空比与幅值都不可能完全相同；而半方波激励下的波形（图7（d））呈现较为理想的正弦波，且幅值比前者大一倍多，分析其原因为，半方波波形较方波更为简单，波形越简单则其在电路中产生的干扰势必也会更小。因此，采用半方波激励，可以获得比方波激励更为理想的检测波形，可以更好地反映被测电流的大小，提高了传感器的灵敏度。

本文还对其他激励信号，如正弦波和锯齿波分别进行了半波变化后作为激励源进行实验，并获得了相应的检测信号（实验中所使用的激励源信号频率均为10 kHz），如图8与图9所示，图8（a）为半正弦波激励信号作为传感器激励信号，可以得到频率为10 kHZ反映被测直流信号大小和方向的一次谐波，图9（a）为半锯齿波激励信号作为传感器激励信号，同样可以得到频率为10 kHZ反映被测直流信号大小和方向的一次谐波。实验结果表明，采用半正弦波和半锯齿波激励均可获得较为理想的一次谐波检测信号。

图7 方波与半方波激励下实验检测波形图

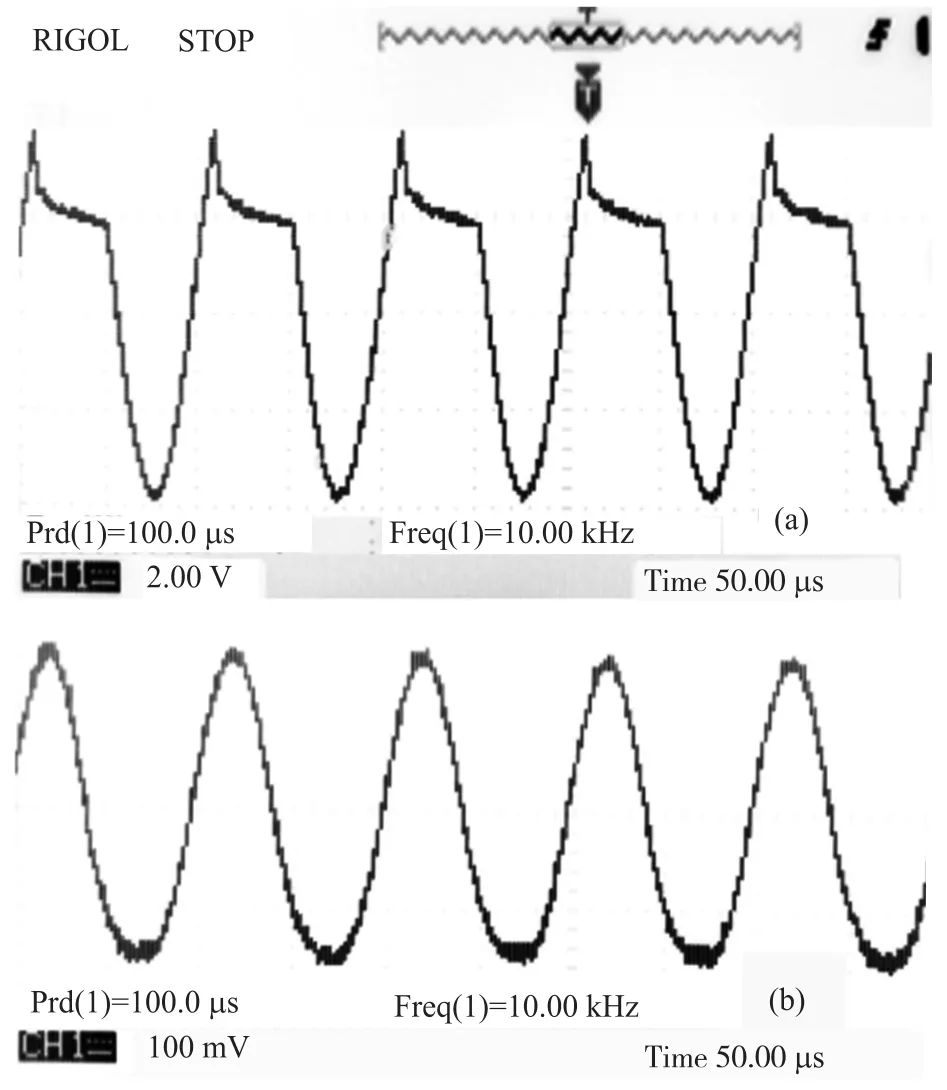
图8 半正弦波及其检测信号

图9 半锯齿波及其检测信号

最后，将此一次谐波进行整形放大后输出，经过测量可以得到的最小额定输入电流为2 mA，额定输出5 V，对比现有通用的额定输出电压为5 V的直流漏电流传感器的最小额定输入电流，得到表1。从表1可以看到传感器灵敏度有所提高。

表1 最小额定输入电流比较

5 结论

本文基于磁调制传感器的工作原理，分析了方波与半方波激励下检测信号的波形数学表达式，提出了采用半波激励简化设计双磁芯差动结构磁调制传感器电路的方法，并分别采用方波、正弦波和锯齿波及其对应半波作为激励信号进行了实验验证。结果表明，采用半波激励可获得频率为一次谐波的检测信号，由于对一次谐波进行相敏检波时，参考信号不需要做倍频处理，所以传感器的信号处理电路结构更为简单，实现了优化设计，且可以减少倍频电路产生的信号干扰，提高了器件的灵敏度。

［1］杨风开.磁调制式直流小电流有源传感器［J］.仪表技术与传感器，2008（10）：9-11.

［2］李亮，阙沛文，陈亮.新型霍尔传感器在电流检测中的应用［J］.仪表技术与传感器，2005（4）：3-7.

［3］Cheng-Fa Cheng，Rong-Sing Li，Jyue-Ru Chen.Design of the DC Leakage Current Sensor with Magnetic Modulation-Based Scheme［J］.IEEE International Symposium，2013（2）：1053-1058.

［4］Yan-Ting Chen，Chih-Cheng Lu，Guo-Ming Sung，et al.Design and Implementation of Driving Circuits for Micro Fluxgate Sen⁃sors Employing Multiple-Harmonic Characteristics［J］.Nano/Mi⁃cro Engineered and Molecular Systems，2011（1）：1071-1074.

［5］Sonoda T，Ueda R，Koga K.An AC and DC Current Sensor of High Accuracy［J］.IEEE Transactions on Industry Applications，1992，28（5）：1087-1094.

［6］冯文光，刘诗斌，李菊萍.数字磁通门传感器的自动相位对准［J］.传感技术学报，2012，25（2）：202-2014.

［7］Min Yingzong，Du Feng，Chen Weigang，et al.An AC/DC Sens⁃ing Method Based on Adaptive Magnetic Modulation Technology with Double Feedback Properties［J］.IEEE International Work⁃shop on Applied Measurements for Power Systems，2011（2）：48-52.

［8］孙晓燕，刘诗斌，刘仕伟.一种迟滞时间差型磁通门检测方法［J］.传感技术学报，2013，26（9）：1202-1205.

［9］郭志友，孙慧卿.磁传感器及其应用［J］.传感器技术，2002，21（7）：56-57.

［10］郭来祥.磁调制器的理论与计算［J］.电测与仪表，1978（2）：20-26.

［11］杨建中，尤政，刘刚，等.微型磁通门式磁敏感器（MEMSMag）［J］.功能材料与器件学报，2008，14（2）：313-318.

［12］侯晓伟，刘诗斌，李菊萍，等.磁通门的数值分析与HSPICE仿真［J］.传感技术学报，2013，26（6）：810-814.

［13］董新平，冯烜，张承燕.一种新型磁通门磁强计［J］.传感器技术，1999，18（6）：34-36.

［14］向小民，曾维鲁，高学军.一种新式磁调制直流电流测量方法［J］.华中理工大学学报，1998，26（12）：65-67.

［15］李前，毛承雄，陆继明，等.磁调制器的建模与仿真研究［J］.传感器技术，2005，24（2）：29-31.

［16］丁扣祥，王维，徐立.基于单磁芯结构的磁调制式直流漏电流互感器［J］.信息技术，2014（3）：131-133.

王隆伟（1990-），男，华中科技大学光学与电子信息学院研究生，主要研究方向为电流传感器，m201371989@hust.edu.cn；

王 鲜（1978-），男，博士，现为华中科技大学光学与电子信息学院副教授，主要研究方向为微波磁学与磁电子技术，wangx@hust.edu.cn。

A Simplified Design and Experimental Verification of the Magnetic Modulation Sensor Based on Half Wave Excitation Signals

WANG Longwei，WANG Xian*，FENG Zekun
（School of Optical and Electronic Information，Huazhong University of Science and Technology，Wuhan 430074，China）

On the basis of the working principle of magnetic modulation sensor，we proposed a method to simplify the magnetic modulation sensor with dual core differential structure by using a half wave excitation signal.Com⁃pared to those using full wave excitation signal，the signal in test port changes from second harmonic into fundamen⁃tal harmonic when using a half wave excitation signal.As a result，frequency multiplication circuit can be omitted since the

ignal frequency does not need to be doubled in Phase-sensitive detection circuit in this case.To verify the above design，full wave of square wave，sine wave，sawtooth wave and their half waves were used as the ex⁃citation signal in the experiment，respectively.The results show that all the half wave excitation signals can realize more symmetrical and ideal detection wave in comparison with the corresponding full wave signals.Therefore，half wave excitation is more conductive to measure the current and simultaneously increase the sensitivity of the magnet⁃ic modulation sensor.

magnetic modulation；second harmonic；fundamental harmonic；Half wave excitation signal

TP212.1

A

1004-1699（2015)10-1448-06

��7230

10.3969/j.issn.1004-1699.2015.10.005

2015-04-17 修改日期：2015-07-28