一种求解兰姆波特征方程的改进方法

何吕龙，尚柏林，张亚豪

（空军工程大学航空航天工程学院，西安710038）

一种求解兰姆波特征方程的改进方法

何吕龙，尚柏林，张亚豪

（空军工程大学航空航天工程学院，西安710038）

针对Rayleigh-Lamb波动方程求解过程中存在分母为零和正切函数间断点的问题，对原有求解方法和解的数据存储结构进行了改进，并使用该改进方法绘制了单层铝合金板中兰姆波的相速度和群速度频散曲线。通过与实验结果进行对比，验证了方法的合理性和正确性。仿真分析结果表明，改进的求解方法在不增加其他约束的情况下，减小了数学分析的难度，降低了程序设计的复杂程度，节约了程序运行时间；改进的数据存储结构可以根据工程需要方便地绘制指定模式的频散曲线，对基于兰姆波的主动结构健康监测系统研究中激励信号中心频率的选取也有一定的指导作用。

兰姆波，频散曲线，健康监测，损伤定位

0　引言

传统的结构健康监测系统（Structural Health Monitoring System，SHMS）大多基于被动无损检测/评估技术（NDT/NDE），需要大量专业仪器。由于这些仪器大多体积较大，结构复杂，重量较大，一般不能实现对结构健康状态的实时在线监测，尤其是针对飞机、飞船等对结构重量要求严格的航空、航天飞行器。因此，发展一种体积小、重量轻的在线结构健康监测系统是航空航天技术的发展趋势和要求。目前，基于兰姆波（Lamb Waves）的主动结构健康监测被认为是一种最有潜力的在线结构健康监测技术。兰姆波在结构中传播时，结构内部的各种损伤都会引起应力集中，导致裂纹扩展加速。这些损伤以及损伤周围的边界都会引起在结构中传播的兰姆波信号的散射和能量吸收，通过对传感器接收到的损伤信号与健康信号进行对比分析，便可对结构的健康状况做出评定。正是基于这种现象，兰姆波可以被用来对结构中的损伤进行检测和定位。与基于声发射的结构健康监测原理类似，基于兰姆波的损伤定位也是通过不同位置的传感器接收到的损伤反射信号与健康信号的时间延迟进行损伤定位的［1］。由于兰姆波具有多模式和频散特性，使得对损伤信号的分析处理变得困难。因此，想要有效利用兰姆波进行损伤定位，必须首先解决兰姆波的频散曲线绘制问题。

兰姆波频散曲线的求解主要有数值计算和试验两种方法，国内外学者对此也做了大量的研究工作。刘增华等［2］借鉴文献［3］中求解多层板结构频散方程的方法，提出采用子波法对自由板的Navier运动方程进行求解来绘制兰姆波频散曲线。徐西宁等在文献［4-5］中分别采用半解析有限元法和图解法得到了兰姆波的频散曲线。数值计算法具有成本低，速度快，精度可控等优点，是求解兰姆波频散方程的常用方法。由于绘制完整的满足工程需要的兰姆波频散曲线需要大量的数据点，采用实验方法周期长，成本高，误差大，一般只能绘制低阶模式的频散曲线，因此，试验方法主要用于检验确认数值计算结果的准确性。虽然以上方法都可以得到兰姆波的频散曲线，但是这些方法都较为复杂，很难被一般工程技术人员理解应用。解的数据存储结构也不够合理，不能根据实际需要绘制指定模式的频散曲线。

针对以上问题，本文对原有求解方法和解的数据存储结构进行了改进，使之更适合一般工程技术人员使用。通过与实验结果进行对比，验证了本文方法的合理性和正确性，对基于兰姆波的主动结构健康监测系统研究中激励信号中心频率的选取也有一定的指导作用。

1　兰姆波特征方程分析

1.1Rayleigh-Lamb波动方程

兰姆波，也即板波，是在作为波导的具有表面边界的板中传播的弹性应力波［6］。由于兰姆波是介质中横波和纵波遇到板的上、下表面时发生波形转换形成的不同波形相互叠加生成的，因此，兰姆波具有多模式和频散特性。在均质薄板中，根据质点振动位移特点，兰姆波可分为对称和反对称两种模式，通常用S0，A0，S1，A1…Sn，An表示，其中Sn表示对称模式，An表示放对称模式，其波动特性采用Rayleigh-Lamb波动方程描述如式（1）、式（2）所示［7］。

对称模式：

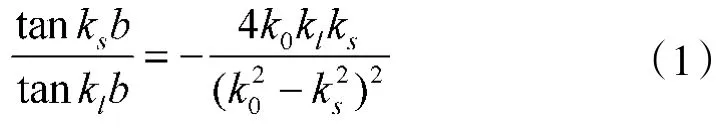
反对称模式：

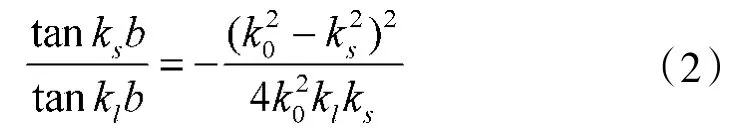
式中，

可以看出，式（1）、式（2）是两个复杂的超越方程。k0与ω的关系是非线性的，而且对不同的模式也对应不同的非线性关系，这也从数学角度证明了兰姆波的多模式和频散特性。因此，对兰姆波在板结构中的传播特性的完整描述通常是一系列分散曲线形式，作为频厚积的函数来表示板结构中兰姆波传播模式的速度，每条曲线代表一种特定的模式，这就是兰姆波的频散曲线［8］。

兰姆波在材料中传播时会发生频散，是一种多模式复合波，相速度即是指各个分波的传播速度，用cp表示。不同模式、相位相同的振动会相互叠加，这种相同相位振动的传播速度就是波群传播的速度，即兰姆波的群速度，用cg表示。群速度可以通过相速度来求解，相速度与群速度的关系如式（5）所示：

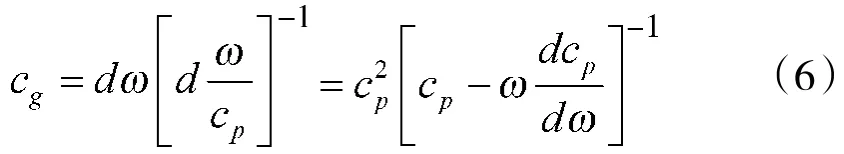
将ω=2πf带入上式得到：

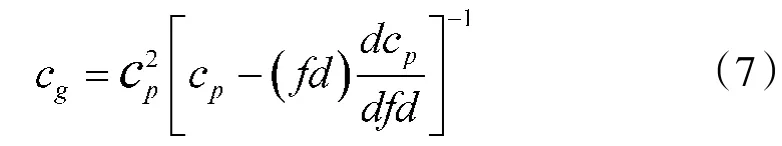
式中，d为薄板厚度，fd表示频率与厚度的乘积，为了便于处理，通常可作为一个参数处理，称为频厚积。频厚积的单位为赫兹·米（Hz·m），但大多数情况，所研究的薄板厚度都在毫米量级，因此，通常用兆赫兹·毫米（MHz·mm）作为fd单位。

1.2Rayleigh-Lamb波动方程分析

观察式（1）、式（2）不难发现，随着cp取值不同，方程两边都可能会出现复数、分母为零、正切函数间断点等问题。在考虑实际物理意义绘制频散曲线时，只需在实数范围内求解方程。本文以对称模式方程为例进行分析，反对称模式同理可得。

将式（3）、式（4）分别带入式（1），得到：

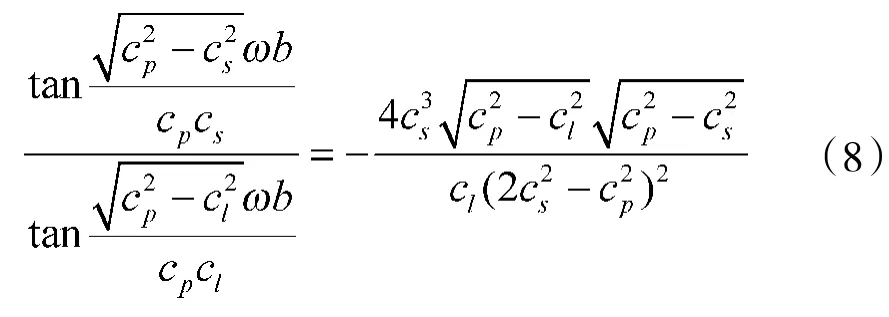
对于均匀薄板，有式（9）成立:

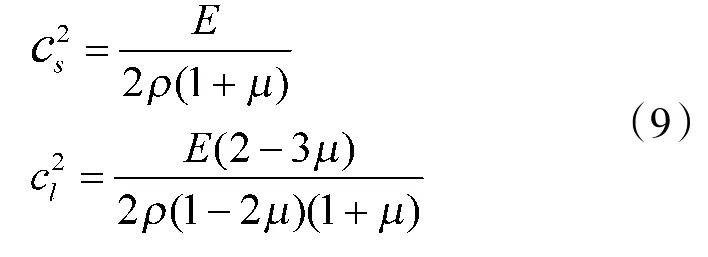
式中，μ为泊松比，ρ为密度。容易证明cl>cs恒成立，因此，在方程求解时，只需对cp进行分段处理。

①0＜cp＜cs

当cp在（0，cs）内取值时，由式（8）可得：

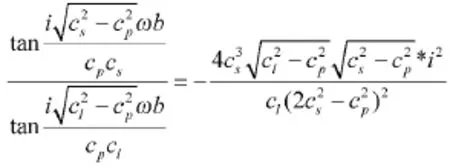
化简可得：

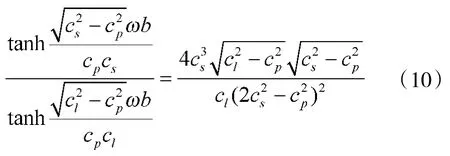
②cs＜cp＜cl

当cp在（cs，cl）内取值时，由式（8）可得：

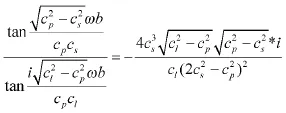
方程两边同乘复数单位i，化简可得：

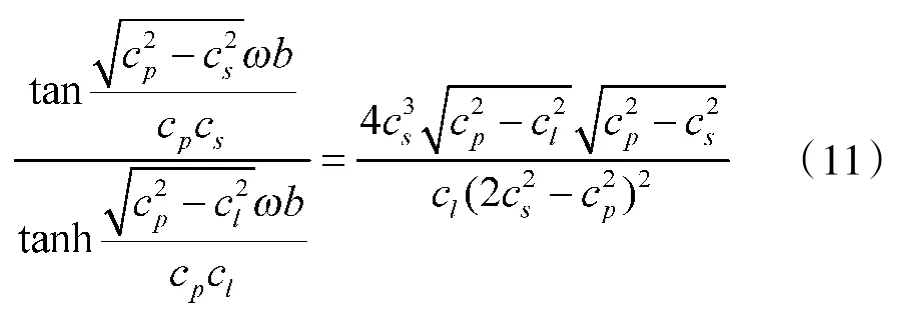
③cp＞cl

当cp在（cl，+∞）内取值时，原方程不变，即：

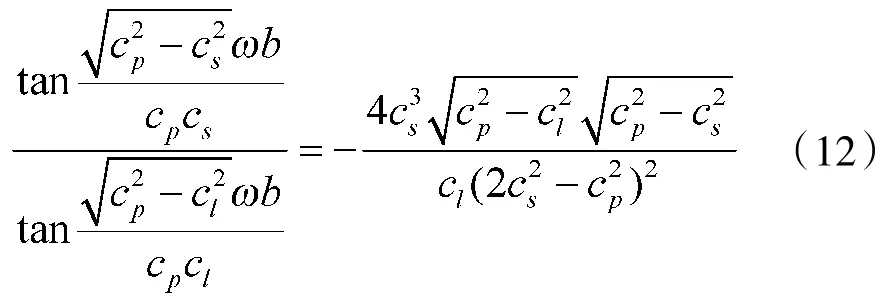
2　改进算法

2.1改进求解方法

观察式（10）～式（12）并结合正切函数的性质，不难发现：

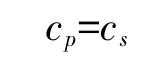
和

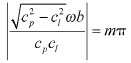
都是方程分母的零点。

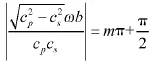
和

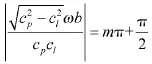
都是方程左边的正切函数的间断点。

这两个问题都是数值求解兰姆波频散曲线时必须考虑的，否则会导致求解结果不严谨，甚至出现错误。

式中，系数A、B、C、D随cp的取值范围不同而变化。

这种处理方法虽然避免了分母为零的情况，通过合理设置迭代步长，也得到了兰姆波频散曲线，但是并没有消除正切函数间断点的影响，求解过程并不严谨，必须合理设置求解步长，以避免正切函数出现间断点。

文献［10］中根据正切函数的性质，首先利用间断点进一步将求解区间划分为若干子区间，然后再在每一个子区间内进行求解。但是，由于兰姆波的多模式和频散特性，使用这种方法需要经过复杂的数学分析，讨论函数间断点，得出多个求解区间，并且区间长度随模式不同而变化，使编程求解变得更加困难，不适合一般工程技术人员使用。如果数学分析时漏掉某一区间，还可能导致绘制的频散曲线不完整。

针对上述问题，本文利用三角函数的性质，将式（10）～式（12）进一步转化为如下形式：

式中，系数A、B、C、D随cp的取值范围不同而变化。

这种处理方法同时避免了分母为零和正切函数存在间断点的问题。编程求解时，不再需要经过复杂的数学分析确定分段点和求解子区间，除了实际物理意义，也没有增加其他约束条件，使得数学分析和程序设计的难度都明显降低。

在绘制群速度频散曲线时，由于数值计算得到的相速度频散曲线是一系列离散点构成，无法求导。如果将这些点进行曲线拟合，不仅需要大量的时间，还会带来较大的误差。为了得到群速度频散曲线，从导数的数学定义出发，采用如下所示近似方法。

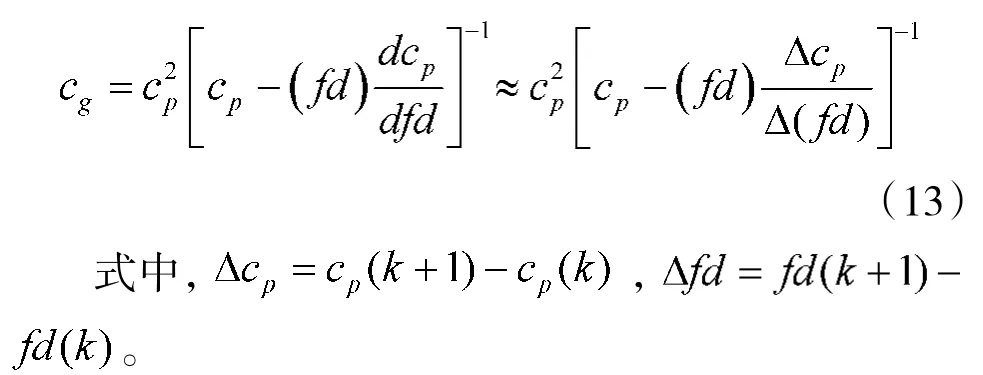
显然，当Δcp、Δfd足够小时，这种近似方法是合理的。

2.2改进解的存储结构

文献［8-10］都通过数值计算方法得到了兰姆波的频散曲线，但是在对这些数值解的存储时都采用简单的数组存储，这使得必须一次绘制出所有的数据点才能得出各个模式兰姆波的频散曲线，但是在实际工程应用中，人们往往只需要特定模式的频散曲线，因此，这种存储方式不能满足工程需要。

为解决这个问题，本文将数据存入矩阵C中：

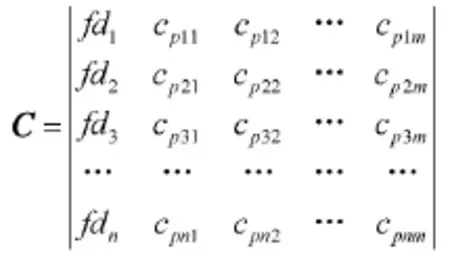
其中，C的第1列为频厚积fdn，从C的第2列开始，每一列都是一种模式的兰姆波在相应频厚积下的速度（相速度或群速度）。以频厚积fdn为横坐标，相速度为纵坐标，把特定一列的速度值绘制出来就可以得出相应模式的频散曲线了，这样就不必再绘制出所有模式的频散曲线或者使用其他数据归类算法，使频散曲线的绘制更加简便、灵活。图1为通过这种方法选择绘制的对称模式S0和S1。

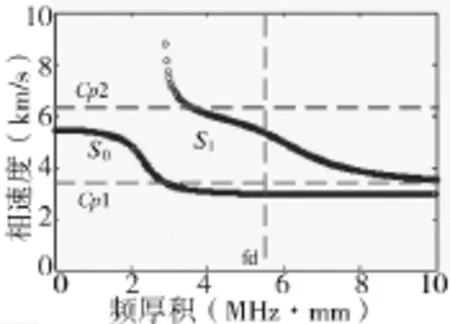
图1　对称模式频散曲线

通过这种数据存储结构，与式（13）的近似方法相结合，可以非常方便地由相速度频散曲线得到群速度频散曲线。如果采用文献［9-10］中简单数组存储方式，则这种近似方法就不能使用了。

3　改进效果分析

3.1算例分析

为了验证本文所用方法的合理性和改进效果，以飞机上大量使用的铝合金板（cl=6 450 m/s，cs=3 090 m/s）为例，通过仿真计算，绘制了铝合金板中的相速度和群速度频散曲线。

将ω=2πf带入式（10）～式（12），三式均是cp和fd的函数。在程序设计时，有两种循环方式可以选择，一种是以cp为外层循环，另一种是以fd为外层循环。如图1所示，若任取cp，对fd由小到大取值，当cp=cp1时，所求得的第1个解对应对称模式S0，当cp=cp2时，求得的第1个解对应对称模式S1，两者对应不同模式。反之，若任取fd，对cp由小到大取值，求得的第1个解始终对应对称模式S0，第2个解始终对应对称模式S1，以此类推。因此，为方便数据存储和曲线绘制，选择以fd为外层循环，cp为内层循环，并利用根的存在判定定理和二分法快速求解方程的根，将最终的计算结果存入矩阵C中。方程解的个数可以通过步长Δcp、Δfd来控制。为节约程序运行时间，程序中设置了最大迭代次数和求解精度两个迭代终止条件，当迭代次数或者求解精度达到程序设定值，迭代便停止，进入下一步。完整的程序框图如下页图2所示。

3.2效果分析

文献［9］中的处理方法虽然避免了分母为零的情况，但是没有消除正切函数间断点的影响。在编程求解时，对迭代步长较为敏感，需要合理选择步长，迭代前需判定是否为间断点。

文献［10］利用间断点进一步将求解区间划分为若干子区间，在每一个子区间内进行求解。但是，由于兰姆波的多模式和频散特性，这种方法需要经过复杂的数学分析，得出多个求解区间，并且区间长度随模式变化而变化，使编程求解变得困难，如果分析错误还可能导致绘制的频散曲线不完整。

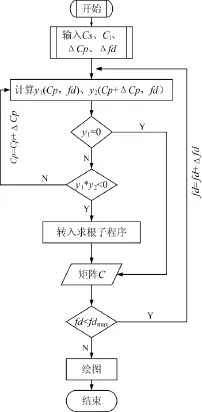
图2　程序设计框图

本文提出的改进方法与文献［8-10］相比，不仅同时避免了分母为零和正切函数存在间断点的问题，而且在编程求解之前，也不需要经过复杂的数学分析确定分段点和求解子区间，除了实际物理意义，没有其他约束条件，使得数学分析和程序设计的难度都明显降低。

在程序运行效率方面，通过编程验证，在相同运行环境和求解精度下，文献［9］中所用算法的运行时间为8.45 s，文献［10］中所用算法的运行时间为12.36 s。虽然改进后的方法方程的长度增加，但是方程中不含tan和tanh，程序运行时间较文献［9］所述方法运行时间减少，降至7.33 s。与文献［10］所述方法相比，因为求解前不需要计算间断点和求解区间，程序运行时间减少更加明显。

通过以上分析可知，与原方法相比，改进后的方法数学分析难度和程序设计复杂性都得到降低，程序运行时间也得到减少。最终绘制的完整的相速度和群速度频散曲线分别如图3（a）、图3（b）所示。图中，S、A分别表示对称和反对称模式，下标0、1、2…分别表示对应模式阶数。

4　结束语

根据Rayleigh-Lamb波动方程的特点，对其求解方法和解的数据存储结构进行了改进，消除了原方程存在的分母为零和正切函数不连续带来的问题，使频散曲线绘制更加简便、灵活，通过实例分析，取得了如下结论：

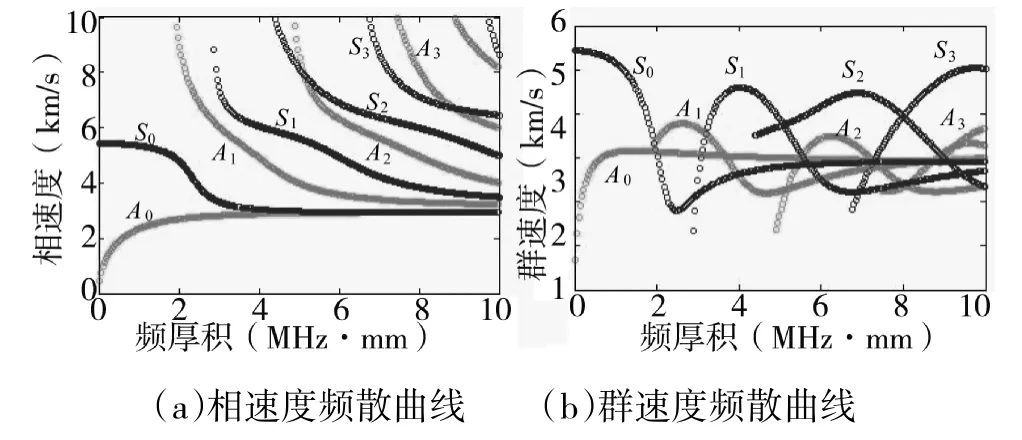
图3　兰姆波频散曲线

①通过与参考文献［8-10］结果进行对比，可知本文提出的改进算法是合理可行的，计算结果是正确无误的，能够正确求解并绘出兰姆波频散曲线，且本文使用的方法在数学分析和编程时都更为简单；②观察图3（a）可知，除对称模式S0和反对称模式A0外，其他模式的兰姆波都存在比较明显的截止频率，频率低于截止频率的兰姆波将不能在介质中传播。这对于主动结构健康监测系统中选择激励信号中心频率，减少多模式信号干扰具有指导作用；③观察图3（b）可知，不同模式兰姆波群速度随频厚积的变化规律不同。应将激励信号中心频率选在频散曲线随频厚积变化平缓的区间，可以减小损伤定位的误差，提高损伤定位精度和对细小裂纹的识别能力。从图中看，当频厚积大于1 MHz·mm时，反对称模式A0群速度几乎不再变化，不考虑其他因素时是最理想的激励信号。

［1］袁慎芳.结构健康监控［M］.北京：国防工业出版社，2007: 221.

［2］刘增华，何存富，吴斌.单层板频散曲线的矩阵表示及Matlab实现［J］.无损检测，2005，27（5）:225-227.

［3］Lowe M J S.Matrix Techniques for Modeling Ultrasonic Waves in Multilayered Media［J］.IEEE Transactions on Ultrasonics，Ferroelectrics and Frequency Control，1995，42（4）:525-542.

［4］徐西宁，余祖俊，朱力强，等.半解析有限元法分析兰姆波频散特性［J］.仪器仪表学报，2013，34（2）：247-253.

［5］徐西宁，余祖俊，朱力强.图解法求解Lamb波频散方程［J］.电子测量与仪器学报，2012，26（11）：966-971.

［6］张海燕，他得安，刘镇清.层状各向异性复合板中的兰姆波［M］.北京:科学出版社，2008:3.

［7］阎石，张海凤，蒙彦宇.Lamb波频散曲线的数值计算及实验验证［J］.华中科技大学学报（城市科学版），2010，27（1）:1-4.

［8］邱雷.基于压电阵列的飞机结构健康监测与管理系统研究［D］.南京:南京航空航天大学，2011.

［9］艾春安，李剑.兰姆波频率方程的数值解法［J］.无损检测，2005，27（6）:294-296.

［10］郑祥明，赵玉珍，史耀武.兰姆波频散曲线的计算［J］.无损检测，2003，25（2）:66-68.

An Improved Method for Solving Lamb Frequency Dispersion Equation

HE Lü-long，SHANG Bo-lin，ZHANG Ya-hao
（School of Aeronautics and Astronautics Engineering，Air Force Engineering University，Xi'an 710038，China）

In order to avoid the zero denominator and existing of discontinuous points in solving Rayleigh-Lamb wave equation，an advanced calculation method and data saving structure are promoted. The frequency dispersion curves of phase velocity and group velocity in an monolayer aluminum plate are plotted respectively，contrastive analysis shows the results are in good agreement with experimental data，which verifies the rationality and accuracy of the improved method.The analysis result demonstrates the improved method can decrease the difficulty of mathematics analysis，lower the complexity of program design，save the calculating time with no additional constraint.The new data saving structure can plot the specified mode of dispersion curves easily，which helps to choose the central frequency of drive signal in an active structural health monitoring system based on Lamb wave.

lamb waves，dispersion curves，structural healthy monitoring，damage location

TG115.28

A

1002-0640（2015）08-0101-05

2014-07-05

2014-08-06

何吕龙（1990-），男，四川绵阳人，硕士研究生。研究方向：飞机结构健康监控。