无序量测下的机动弱目标检测前跟踪*

谭顺成，王国宏，于洪波，关成斌

（海军航空工程学院信息融合技术研究所，山东烟台264001）

无序量测下的机动弱目标检测前跟踪*

谭顺成，王国宏，于洪波，关成斌

（海军航空工程学院信息融合技术研究所，山东烟台264001）

针对无序量测（OOSM）情况下的机动微弱目标检测与跟踪问题，提出一种基于OOSM和多模粒子滤波（OOSM-MMPF）的检测前跟踪（TBD）算法。该算法通过直接利用OOSM对粒子权重进行更新，并在此基础上对粒子集进行重采样，从而实现OOSM情况下的目标状态更新。由于充分利用了OOSM包含的信息，该算法可以有效提高机动微弱目标的正确检测概率与跟踪精度。仿真结果表明，该算法可以有效处理OOSM问题，实现对机动弱目标的有效检测和跟踪，其算法性能接近顺序量测滤波时的MMPF算法性能。

无序量测，多模粒子滤波，检测前跟踪，机动弱目标

0　引言

检测前跟踪（TBD）［1-7］算法通过充分利用原始量测数据信息，可以有效实现低信噪比情况下的微弱目标检测与跟踪。典型的TBD算法主要有动态规划［2］、Hough变换［3］、极大似然［4］以及粒子滤波（PF）［5］等。其中，基于PF的TBD方法由于对非线性非高斯系统具有较强的适应性和简单易行等突出优点，得到越来越广泛的关注和应用［5-7］。

然而，在集中式融合跟踪系统中，局部传感器对信号进行测量，然后将观测到的目标量测送至融合中心，由于各传感器不同的量测预处理时间以及通信延迟等因素的影响，各传感器的量测并不一定能按照其被观测到的时间顺序到达融合中心，即出现较早时刻的量测在较晚时刻到达融合中心，从而出现所谓的无序量测（OOSM）问题［8-9］。若在整个融合跟踪系统中，所有传感器的量测最多延迟一步到达，则称之为一步延迟OOSM问题；若传感器的量测可延迟多步到达，则称之为多步延迟OOSM问题。

为了解决OOSM情况下的目标状态更新问题，国内外已有较多的专家和学者进行了大量的研究［9-16］。Hilton等首次提出了一种适应于单步延迟OOSM的次优滤波方法，而Bar-Shalom等随之提出了一种适应于单步延迟OOSM的最优算法，即A1算法［9］，同时将Hilton等提出的算法命名为B1算法，并给出了次优的C1算法，随后Bar-Shalom等随后又通过构建等效量测的思想，将A1、B1以及C1算法推广至多步延迟的情况，即Al1、Bl1和Cl1算法［10］。Orton等人则研究了基于PF的OOSM更新算法［11-12］；文献［13］证明A1算法在过程噪声直接离散化模型（DDM）条件下不是最优的，并提出了一种与过程噪声离散化模型无关的最优OOSM滤波算法；文献［14］研究了无序量测系统的最优网络化状态估计方法；文献［15］研究了一种组合“前向预测”和“等价量测”的OOSM方法；文献［16］研究了一种基于不敏变换的单步滞后OOSM算法。

1　基于OOSM-MMPF的TBD方法

1.1系统模型

对应于匀速直线运动（CV）模型

对应于坐标转动（CT）模型，式中T为传感器扫描周期

分别对应于顺时针CT和逆时针CT，αm>0是机动加速度。

假设目标某一时刻只遵循一种运动模型，各种运动模型之间的转换可描述为3态的1阶Markov链。模型转移概率矩阵为∏m，其各元素

表示模型i到模型j的转移概率。定义φ1= P{r1=1}，φ2=P{r1=2}，φ3=P{r1=3}（满足φ1+φ2+φ3=1），表示目标刚出现时分别按3种模式运动的概率。

此外，时刻k监测区域内可能存在目标，也可能不存在目标，可以描述为2态的1阶Markov链。以变量Ek对此建模，Ek=0表示目标不存在，Ek=1表示目标存在。假设目标初始存在概率η1=P{E1=1}已知，目标“新生”概率Pb和“死亡”概率Pd分别定义为：

其转换概率矩阵为：

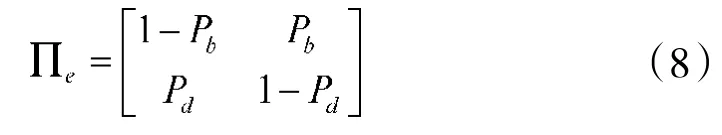
假设传感器提供的量测数据为监控区域的二维图像，每张图像包含m×n个分辨单元。每个分辨单元对应于一个Δx×Δy的区域，第（i，j）个单元的中心定义为（iΔx，jΔy），（i=1，…，m，j=1，…，n）。以zk（i，j）表示时刻k分辨单元（i，j）的观测数据

其中

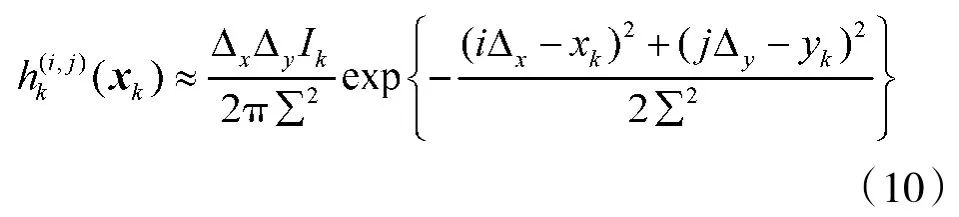
wk（i，j）为分辨单元（i，j）的量测噪声，并假设分辨单元之间以及时刻间量测噪声相互独立，∑为传感器模糊系数。则k时刻的量测可以表述为，直到k时刻的完整观测数据集合表示为。根据传感器观测模型，似然函数可以表述如下［5］

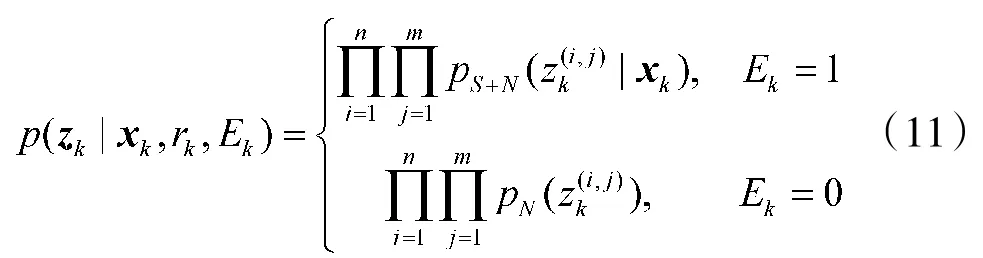
由于目标仅对（xk，yk）附近的分辨单元有影响，p（zk|xk，rk，Ek=1）可以近似表示为：

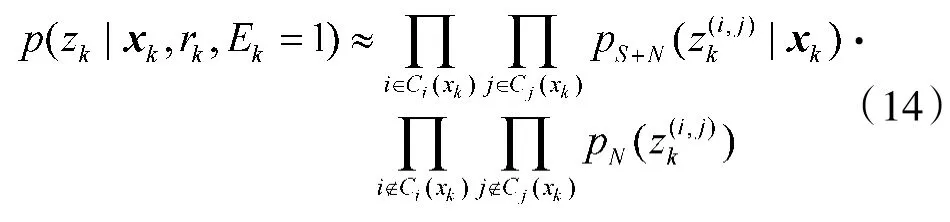
这里Ci（xk）和Cj（xk）表示所有受目标影响的分辨单元坐标（i，j）的集合。

1.2OOSM下的粒子权重更新

假设k时刻的量测zk被确定为无序量测，即其被观测到的时刻满足tk＜tk-1。令a和b分别表示OOSM之前和之后顺序量测的观测时刻，且满足tb＜tk＜ta和a=b+1。引入混合状态向量，给定k-1时刻目标估计的联合后验密度p（y0：k-1| z1：k-1）和OOSM zk，k时刻目标估计的联合后验密度可以表示为

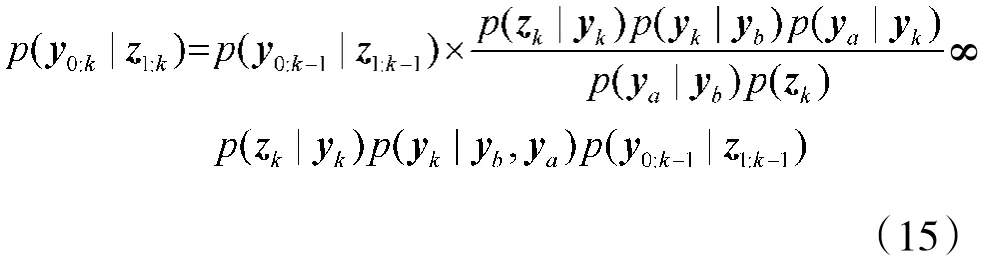
若选取p（yk|ya，yb）为重要性采样函数，式（16）可以简化为

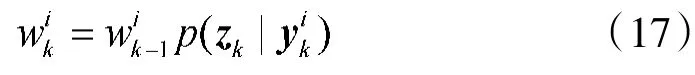
其中

1.3OOSM-MMPF的TBD算法实现

令Ωk={Sl：k}表示滤波器在k时刻的输入，其中表示p时刻的粒子集，而Sl：k则表示l=max{0，k-lmax}时刻至k时刻所有粒子集的集合，N为滤波器采用的粒子数，lmax为最大延迟步长。基于OOSM-MMPF的TBD算法的基本流程如下所述：

步骤1：k=0，根据目标状态初始分布以及目标运动模型初始分布得到初始化粒子集S0，令Ω0={S0}；

步骤2：令k=k+1，判断zk是否为无序量测，若zk不是OOSM，转步骤3，否则转步骤8；

为避免变量的非平稳性引起伪回归，需要对各个变量进行平稳性检验。面板数据平稳性检验一般通过单位根检验来实现，常常采用两种方法，相同根情形下的LLC(Levin-Lin-Chu)检验和不同根情形下的Fisher-ADF检验。如果只通过了其中一个检验，则面板数据是不平稳的，两种检验结果都表示变量平稳时，面板数据才是平稳的。本文以LLC检验和Fisher-ADF检验对所设定面板模型的各个变量进行检验，结果见表1。由表1可以看出，各变量均表现为一阶单整，即一阶差分数据都是平稳的。

步骤5：粒子权重更新，引入像素似然比［11］

这里hk（i，j）在式（10）中定义，将式（12）与式（13）带入式（22）得

步骤6：粒子重采样

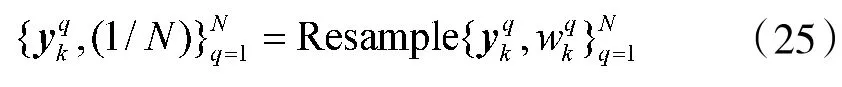
得到Sk，本文在此采用系统重采样法。

步骤7：目标状态估计，首先估计目标存在概率

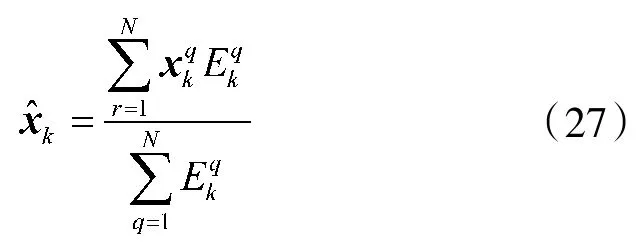
利用Sk对Ωk-1进行更新，得到Ωk，转步骤2。

步骤8：根据OOSM的被观测时刻tk确定OOSM的前一时刻b以及后一时刻a；

步骤9：粒子状态预测及粒子权重更新，对任意q∈{1，2，…，N}同样分两种情况进行讨论：

步骤10：粒子权重更新，利用OOSM和式（23）更新粒子权重，得到粒子权重集，并利用其对粒子状态集重采样，即

值得注意的是，此处仅利用OOSM更新k-1时刻的粒子权重，然后在此基础上对时刻的粒子集进行重采样；

2　实验仿真

本节设置一个与文献［5］相同的机动弱目标的运动场景进行实验仿真，滤波器的基本参数也同文献［5］。不同之处在于文献［5］采用的单传感器，不存在OOSM问题。不失一般性，本文设置两个传感器对目标进行观测，其中传感器1的量测数据可以无延迟地到达融合中心，而传感器2的量测需经过一定的延迟才能到达融合中心。表1描述了融合中心收到量测数据的时序情况，每个量测数据标有观测时刻和传感器ID号。

从表1可以看出，传感器2的量测较传感器1的量测延迟了2个时刻到达，为多步延迟OOSM的情况。图1给出了SNR=6 dB时，传感器1在k=1 s、7 s、20 s、38 s提供的监测区域的灰度图。由仿真条件可知，目标在k=7 s至k=36 s真实存在于监测区域，其他时刻监测区域内不存在目标。但是从图1中并不能直接检测目标存在与否。图2～图4给出了OOSM-MMPF算法随机的1次仿真结果，其中图2给出了算法估计的各时刻的目标存在概率，图中底部的“*”表示该时刻监测区域确实存在目标，图3为算法估计的目标航迹与目标真实点迹的对比，图4则为算法估计的各时刻目标采取各运动模型的概率。若假设某一时刻估计的目标存在概率Pˆk≥0.6便认为该时刻存在目标，从图2可以看出，虽然算法在目标出现后需要经过几个时刻的积累才能检测目标存在，但是一旦算法检测到目标存在时，其估计的目标存在概率迅速增大，接近于1，且当目标消失时，估计的目标存在概率迅速降低，接近于0，算法可以无延迟地检测目标消失。从图4可以看出，算法可以实现对目标运动模型的有效估计，且当目标采取CV运动模型时，算法估计的模型概率最为准确，达到了0.9左右；同时，当目标运动模型从CV转向CT时，CV模型的概率迅速降低至0.5以下，而CT模型的概率则迅速上升，超过CV模型的概率成为主导。

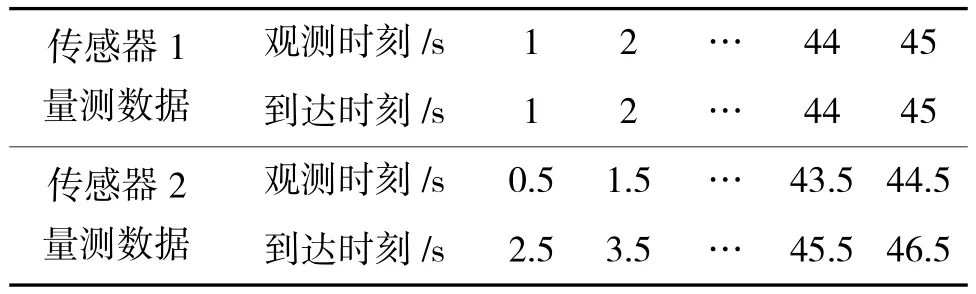
表1　各传感器量测观测时刻和实际到达时刻

图1　SNR=6 dB时的观测图像

图2　估计的目标存在概率

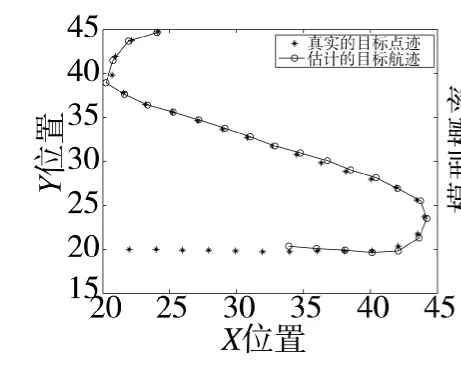
图3　目标真实点迹与估计的航迹

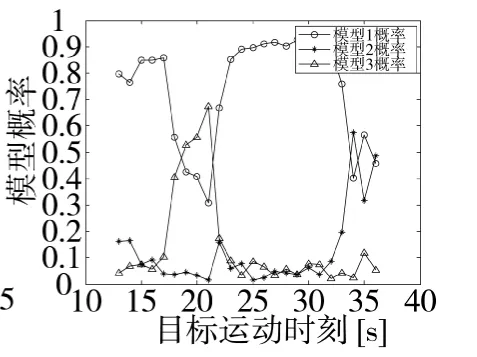
图4　估计的各运动模型概率

为了进一步验证算法的有效性，将本文构造的算法与有序量测下（各传感器的量测均能无延迟到达融合中心）和OOSM下丢弃OOSM的基于MMPF的TBD方法进行仿真分析和比较。为方便描述，此处以MMPFins、MMPFdis以及OOSM-MMPF分别表示有序量测滤波方法、丢弃OOSM方法以及本文算法。图5～图7分别给出了目标信噪比为6 dB时3种算法估计的目标存在概率对比以及滤波达到稳定时估计的目标位置均方根误差（RMSE）和速度RMSE对比，仿真结果为30次Monte Carlo仿真取平均的结果。从仿真结果可以看出，与MMPFdis相比，由于OOSM-MMPF更加充分地利用了OOSM包含的目标信息，该算法具有更好的目标检测性能；同时，与MMPFins相比，OOSM-MMPF估计的目标位置和速度等均方根误差与MMPFins的均方根误差非常接近，因此其目标跟踪性能与MMPFins性能相当。

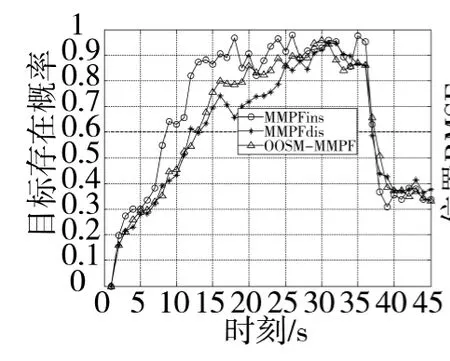
图5　估计的目标存在概率比较

图6　目标位置RMSE比较

图7　目标速度RMSE比较

3　结束语

为解决低信噪比和OOSM情况下的机动目标检测与跟踪问题，本文研究了一种基于OOSM-MMPF的机动弱目标TBD方法。通过有效利用OOSM，该算法可以有效地提高对基于MMPF的TBD算法对机动弱目标的检测和跟踪性能，其目标跟踪精度接近于有序量测滤波算法的目标跟踪精度，且具有较好的稳健性，可应用于多传感器融合跟踪领域。仿真实例表明了算法的可行性和有效性。本文只是重点研究了基于MMPF的TBD算法如何有效利于OOSM进行更新的问题，没有涉及到多传感器量测数据的坐标转换以及不同传感器的不同量测精度等问题，综合考虑这些因素是本文的进一步研究方向之一。

［1］Jishy K，Lehmann F.A Bayesian Track-before-detect Procedure for Passive Radars［J］.EURASIP Journal on Advances in Signal Processing，2013（1）:45.

［2］Yi W，Kong L，Yang J.Student Highlight:Dynamic Programming-based Track-before-detect Approach to Multitarget Tracking［J］.IEEE Aerospace and Electronic Systems Magazine，2012，27（12）:31-33.

［3］Fan L，Zhang X，Wei L.TBD Algorithm Based on Improved Randomized Hough Transform for Dim Target Detection［J］. ProgressinElectromagneticsResearchC，2012，31:271-285.

［4］Orlando D，Ehlers F，Ricci G.A Maximum Likelihood Tracker for Multistatic Sonars［C］//2010 13th Conference on Information Fusion，Edinburgh，2010:1-6.

［5］龚亚信，杨宏文，胡卫东，等.基于多模粒子滤波的机动弱目标检测前跟踪［J］.电子与信息学报，2008，30（4）: 941-944.

［6］Long Y L，Xu H，An W，et al.Track-before-detect for Infrared Maneuvering Dim Multi-target via MM-PHD［J］. Chinese Journal of Aeronautics，2012，25（2）:252-261.

［7］Rutten M G，Gordon N J，Maskell，S.Recursive Track-before-detect with Target Amplitude Fluctuations［J］.IEE Proceedings Radar，Sonar and Navigation，2005，152（5）: 345-352.

［8］王炜，黄心汉，王敏.无序量测滤波更新算法综述［J］.控制与决策，2012，27（1）:1-7，14.

［9］Bar-Shalom Y.Update with out-of-sequence Measurements in Tracking:Exact Solution［J］.IEEE Transactions on Aerospace and Electronic Systems，2002，38（3）:769-778.

［10］Bar-Shalom Y，Chen H M，Mallick M.One-step Solution for the Multistep Out-of-sequence-measurement Problem in Tracking［J］.IEEE Transactions on Aerospace and Electronic Systems，2004，40（1）:27-37.

［11］Orton M，Marrs A.Particle Filters for Tracking with Out-ofsequenceMeasurements［J］.IEEETransactionson Aerospace and Electronic Systems，2005，41（2）:693-702.

［12］Zhang S，Bar-Shalom Y.Out-of-Sequence Measurement Processing for Particle Filter:Exact Bayesian Solution［J］. IEEE Transactions on Aerospace and Electronic Systems，2012，48（4）:2818-2831.

［13］Zhou W H，Li L，Chen G H，et al.Optimality Analysis of One-stepOOSMFilteringAlgorithmsin TargetTracking［J］. ScienceChinaInformationSciences，2007，50（2）:170-187.

［14］葛泉波，冯肖亮，徐廷梁.不确定无序量测系统的最优网络化状态估计［J］.电子学报，2011，39（3A）:7-13.

［15］王炜，黄心汉，徐忠昌，等.一种新的无序量测处理算法［J］.电子与信息学报，2009，31（8）:1996-2000.

［16］王君，闻娟，吴妍岩.机动目标的跟踪滤波处理［J］.四川兵工学报，2013，32（11）:106-108.

［17］Chen J G，Li J，Gao X B.Single-step-lag OOSM Algorithm Based on Unscented Transformation［J］.Science China Information Sciences，2011，54（3）:664-673.

Track-before-detect with Out-of-sequence Measurement for Maneuvering Weak Target

TAN Shun-cheng，WANG Guo-hong，YU Hong-bo，GUAN Cheng-bin
（Institute of Information Fusion Technology，Naval Aeronautical and Astronautical University，Yantai 264001，China）

To address the problem of maneuvering weak target detection and tracking with out-ofsequence measurements（OOSM），a maneuvering weak target track-before-detect method is proposed based on the OOSM and multiple model particle filter（OOSM-MMPF）.By updating the weights of particles directly with the OOSM and performing a resampling step on the particle set，the target state is updated with the OOSM.Due to make full use of the information contained in the OOSM，the proposed method can improve the correct detection probability and tracking performance of target efficiently. Simulation results demonstrate that the proposed method can solve the problem of OOSM and detect and track maneuvering weak target effectively with the performance of target tracking is close to that of MMPF with in-sequence measurements.

out-of-sequence measurement，multiple model particle filter，track-before-detect，maneuvering weak target

TN953

A

1002-0640（2015）08-0014-05

2014-06-25

2014-07-01

国家自然科学基金（61179018，61102165，61102167，61002006）；“泰山学者”建设工程专项经费资助项目

谭顺成（1985-），男，湖南湘潭人，博士。研究方向：信息融合、微弱目标检测与跟踪。