基于RBF神经网络的空中目标识别技术*

刘砚菊，寇国豪，宋建辉

（沈阳理工大学信息科学与工程学院，沈阳110159）

基于RBF神经网络的空中目标识别技术*

刘砚菊，寇国豪，宋建辉

（沈阳理工大学信息科学与工程学院，沈阳110159）

空中目标识别的正确与否对防空火力的部署、分配及有效打击有着重要的意义。利用径向基函数（RBF）神经网络逼近非线性的空中目标识别模型。在RBF神经网络空中目标识别模型中，输入向量是雷达探测到的空中飞行目标的6种目标属性，输出向量是空中飞行目标的类型。通过Matlab的数据仿真结果与传统的BP神经网络目标识别模型相比，该模型的误差更小，可以有效地提高空中目标的识别率。

目标识别，RBF，雷达探测，建模与仿真

0　引言

目标识别是现代防空作战的热点研究内容。在军事领域，需要通过目标识别以提高对潜在威胁进行评估的准确性，特别是准确地鉴别出敌方的目标。从实战角度看，在探测到目标的早期就完成识别出目标的威胁程度和类型将提供更多的反应时间，有利于采取合适的防御性行动。例如，作战过程中判定出威胁目标的实际类型，如战斗机抑或导弹，在选择反击武器时就更能做到“量体裁衣”，有利于节约有限的作战资源［1］。

D-S证据理论在文献［2］的空中目标识别技术中得到了应用；文献［3］构建了粒子群K均值聚类的识别模型；文献［4］引入了支持向量机算法，这种算法可以适用于样本很少的情况；文献［5］建立了灰色识别模型，达到了目标识别的目的。在模式识别领域，人工神经网络技术已经迅速发展成为一种非常有效的方式。在空中目标识别中，目前采用最多的是BP神经网络［6］。由于BP神经网络在进行分类时存在网络学习收敛速度慢、容易陷入局部极小、训练网络不稳定等问题［7］，因此，在目标识别过程中，BP神经网络存在较大的局限性。在逼近能力、分类能力和学习速度方面RBF均优于BP神经网络，前者具有唯一最佳逼近的特性，并且没有局部极小［8］。本文采用径向基函数神经网络的方法逼近非线性空中目标识别模型，用雷达传感器探测目标的运动特性、飞行参数等数据，对目标的类型进行识别。通过与传统的BP神经网络识别模型相比，体现出RBF网络的优越性，降低了目标识别的误差率，达到提高目标识别率的目的。

1　RBF目标识别过程

目标的识别过程如图1所示。

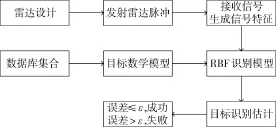
图1　RBF目标识别过程

在选择雷达时，雷达应适合必须执行的测量类型，能够提供需要的目标特征。波形、相关的信号处理、雷达相位噪声和动态范围性能的设计尽可能减少杂波影响。并且，目标反射的回波具有足够的能量，确保雷达可以准确地探测到最小的回波信号。雷达在发射高频脉冲串之后，将会接收到来自目标的回波信号，然后对回波信号进行处理并应用于目标识别过程。

RBF神经网络训练雷达探测到的一部分数据，建立飞行目标的特征数据库。再利用探测到的另一部分目标特征与集成的目标数学模型进行比较，用RBF神经网络识别模型进行识别，区别易混淆的目标信号，达到分辨出目标类型的目的。

2　RBF空中目标识别模型

2.1RBF神经网络结构及算法

径向基函数（RBF，Radial Basis Function）神经网络，是一种局部逼近网络，可以逼近任意精度任意连续函数。RBF网络的第1层为输入层，由信号输入节点组成；第2层为隐含层；第3层为输出层，对输入模式的作用作出响应。RBF和BP网络最大的区别在于，前者有且仅有一个隐含层。

RBF的基本思想是：用RBF作为隐层单元的“基”构成隐层空间，当确定RBF中心后，就可以将输入向量直接映射到隐空间，这种关系是非线性的。输出层是隐单元输出的线性加权和，两者之间通过权连接。本文选取最常用的隐含层节点变换函数高斯函数：

式中σ表示高斯函数的宽度。

由此，可以得出径向基函数神经网络的激活函数：

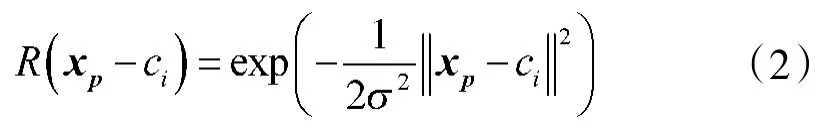
式中：c表示高斯函数的中心；||xp-ci||表示欧式范数；为第p个输入样本，p=1，2，…，P，表示样本的总个数；ci是径向基函数的中心。

由网络的结构可以得到网络的输出为

式中：ωij是隐含层第i个节点到第j个输出的权值；i=1，2，…，h表示隐含层的节点数；yj是与输入样本对应网络的第j个输出节点的实际输出。

RBF神经网络的学习算法主要是求解以下3个参数即基函数的中心位置、宽度和输出单元权值。

定义一个目标函数：

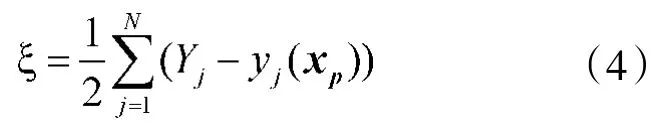
式中：Yj是网络的期望输出；yj（xp）是网络的实际输出；N为训练样本的数量。

网络训练的要求是使得目标函数ξ达到极小的时候，寻求以上3个参数。应用梯度下降法可得：

①径向基函数数据中心算法：

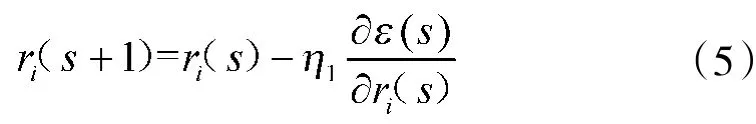
②径向基函数的宽度算法：

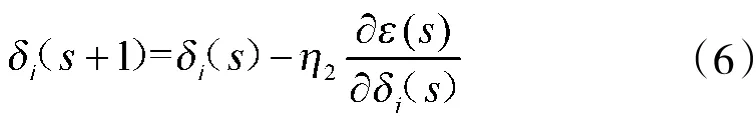
③输出单元的连接权值：

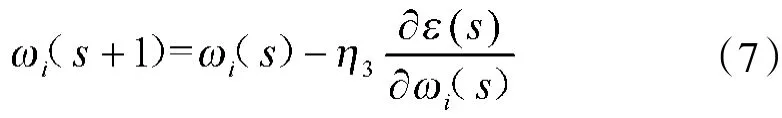
式中：i=1，2，…，h表示隐含层神经元节点数目；η1，η2，η3表示学习速率；s表示s时刻。

2.2RBF空中目标识别模型

雷达传感器可以对目标距离、速度以及方位角和仰角等数据进行测量，所以目标高度也可以通过计算得出。根据目标反射信号的强度，可以推算出目标的截面积，根据该数据又可以推算出目标的大概尺寸。通过雷达所提供的数据，可以识别出目标的类型。文中选取直升机、轰炸机、歼轰机和反舰导弹4种目标进行识别。选择6个参量作为空中目标识别模型的输入，以空中目标的类型作为输出，则可以得到RBF空中目标识别模型的输出：

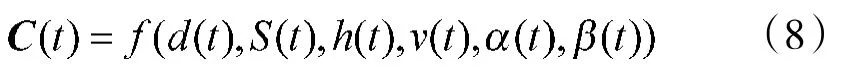
式中：d表示空中目标与雷达天线之间的距离；S表示雷达的反射截面积；h表示空中目标的飞行高度；v表示空中目标的飞行速度；α表示空中目标的方位角；β表示空中目标的俯仰角。设:

由式（3）和式（8）可得RBF空中目标识别模型的输出为

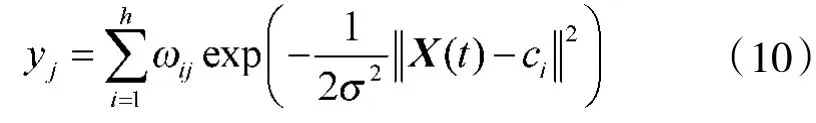
当RBF网络进行模式识别时，输出层节点数的选择可以参考公式log2m，m为待分类目标的总数。因此，本文的输出节点数为2。输出层选取（0.2 0.2），（0.4 0.4），（0.6 0.6），（0.8 0.8）分别代表直升机、轰炸机、歼轰机和反舰导弹。输入层的节点数参考输入参量的个数，选取6。

神经网络设计中非常重要的一个环节就是确定隐含层节点数，整个RBF网络的收敛速度以及网络精度都受到隐含层节点个数的影响。为了使神经网络尽快达到稳定，并且获得较精确的网络输出，合理选取隐含层节点数非常重要。

隐含层节点数往往根据前人的经验进行试验确定。一般认为网络学习后泛化能力变差是由于隐层节点数过多造成的，隐含层节点个数过少，则导致无法产生足够的连接权值组合供网络学习。

文中采用经验式（11）选取隐节点个数

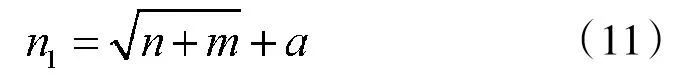
式中：n为输入样本数；m为输出样本数；a=1～10。

根据文中输入输出节点数和网络的不断训练，最终选取的节点数为11。在确定了输入向量、输出向量和隐含层节点数以后，建立的RBF空中目标识别模型，如图2所示。

图2　RBF空中目标识别模型

表1　样本数据归一化处理结果

2.3输入输出向量归一化

输入向量X（t）=（d（t），s（t），h（t），v（t），α（t），β（t）），本文采用效用函数为每一个属性值确定合理的效用值，RBF网络的输入值各因素的效用值即为RBF网络目标识别模型的输入值。

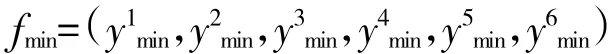
①随着因素值的减小，对目标识别越有利时

②随着因素值的增大，对目标识别越有利时

③当因素值在某一范围内对目标识别有利时，设因素值在（y1，y2）内最好，效用函数为

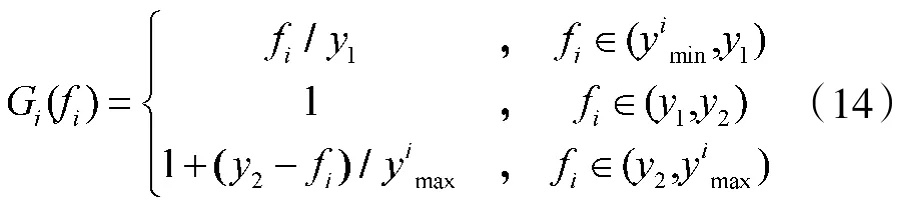
输出向量的处理已经在前面给出，数据处理的结果如表1所示。

3　仿真结果与分析

为了验证RBF神经网络目标识别模型的有效性和实用性，建立一个传统BP神经网络识别模型与其进行对比。BP神经网络选取单隐层的三层结构网络，输入层节点数选择6，隐含层节点数选择4，输出层节点数选择2。输出层、隐含层均采用logsig激活函数，训练算法采用梯度下降法。训练步数为5 000，目标误差为0.001。

分别对两种神经网络空中目标识别模型进行Matlab仿真。选取样本归一化处理结果中数据的前10组数据作为训练样本，后10组数据作为测试样本。

表2是RBF和BP网络模型输出结果的对比。在此，定义误差=|期望输出-实际输出|；误差率=误差/0.2×100%。

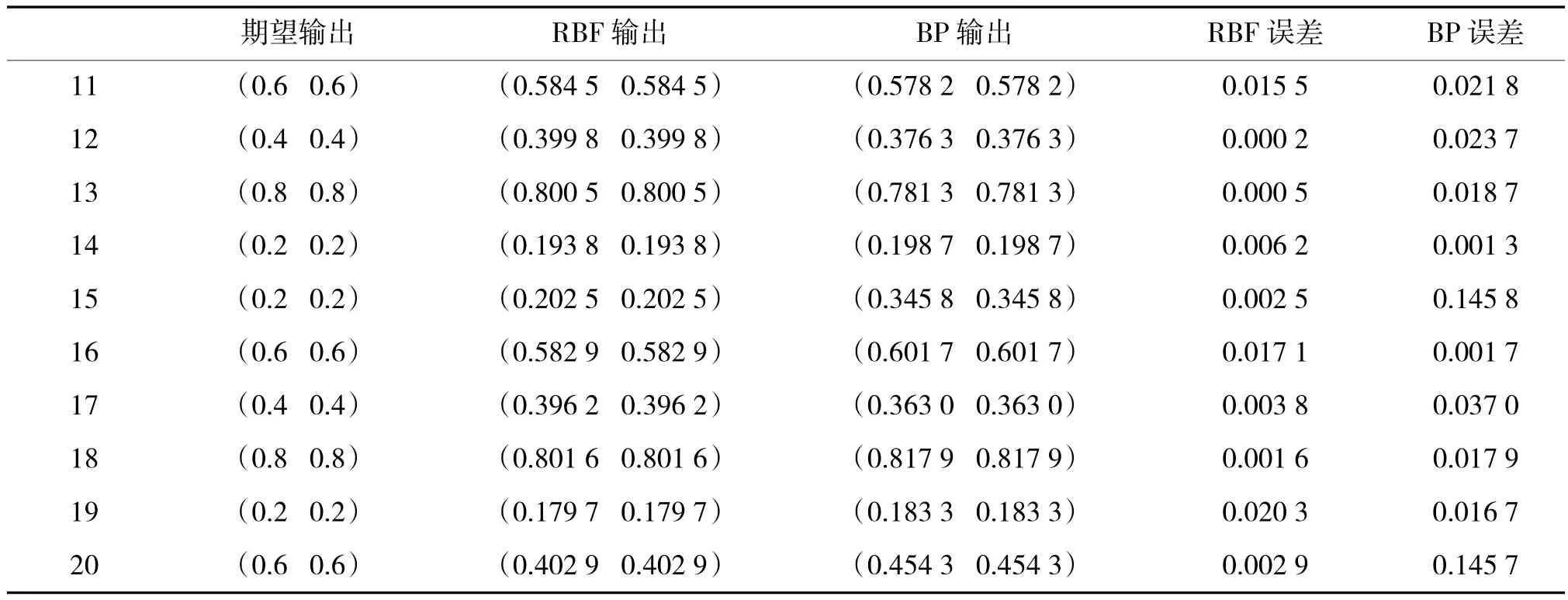
表2　RBF网络识别模型和BP识别模型对比

通过以上输出数据，可以绘制出RBF和BP网络模型的输出预测图，如图3所示。

图3　RBF和BP网络空中目标识别模型输出预测曲线

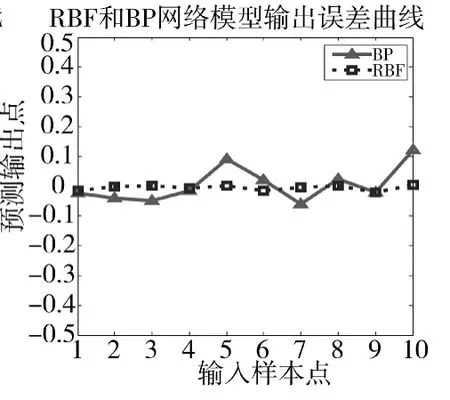
图4　RBF和BP网络模型输出误差曲线对比

RBF和BP网络目标识别模型的输出误差曲线对比如图4所示。

由仿真程序可以得出RBF网络识别模型的输入层到隐层之间的阈值是:［0.83 0.83 0.83 0.83 0.83 0.83 0.83 0.83 0.83 0.83］T;隐层到输出层之间的阈值是［-3.81-3.81］T。输入层到隐层的权值矩阵W1：

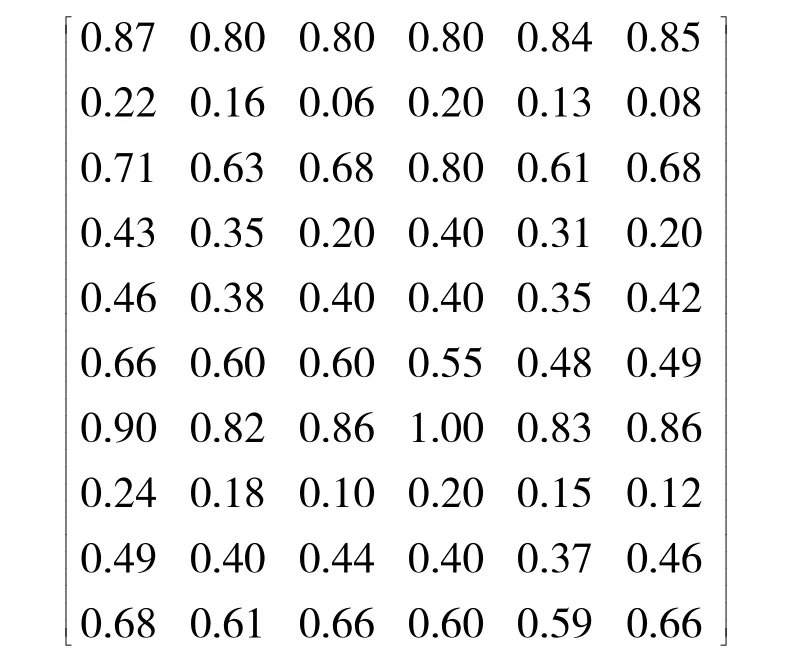
隐层到输出层之间的权值矩阵W2：

决策准则：本文设定目标识别门限ε≤0.05，即（0.15～0.25 0.15～0.25）表示识别出直升机；（0.35～0.45 0.35～0.45）表示识别出轰炸机；（0.55～0.65 0.55～0.65）表示识别出歼轰机；（0.75～0.85 0.75～0.85）表示识别出反舰导弹。由以上数据可以分析得出，RBF网络模型能够准确识别出10组测试数据，而BP网络模型不能准确识别出第15，17，20组数据。故在本次实验中，RBF模型的目标识别率达到100%，虚警率为0；而BP模型的目标识别率仅有70%，虚警率达到30%。RBF模型的平均误差率为0.705%，而BP模型的平均误差率为4.305%，RBF模型的平均误差率远远小于BP模型，在精确率上明显优于后者。再观察两个网络的预测值与样本值误差图，RBF网络模型的曲线比BP网络的更加平缓，RBF网络模型的方差为9.21×10-5，BP网络模型的方差是0.004 6，表明基于RBF网络的空中目标识别模型更加稳定。

下页图5为RBF网络识别模型的收敛图。RBF网络在满足系统要求的情况下，27步迅速完成收敛。而BP网络模型的收敛则相对较慢，在40次左右才完成收敛。另外，在同等条件和环境下，通过统计计算，RBF网络的平均训练时间为1.041 s，BP网络的平均训练时间为1.377 s，表明RBF模型比BP模型实时性更好。当样本数据量更大时，RBF网络模型的优势更加明显。

图5　RBF网络模型收敛图

4　结束语

RBF网络从理论上证明是前向网络中完成映射能力最优的网络。它具有较强的输入输出映射能力，并且收敛速度和学习过程都比BP网络快。本文采用梯度下降法获得RBF网络的数据中心和隐含层到输出层的连接权值。应用处理好的数据训练和校正网络模型，最终得到的RBF神经网络空中目标识别模型具有相当高的精度。

通过空中目标模型的对比，RBF网络模型能够有效地识别出目标，并且保持较好的稳定性，达到了提高目标识别率的目的。下一步，优化RBF神经网络的学习算法，使得学习速度和训练精度得到进一步提高。

［1］Tait P.雷达目标识别导论［M］.罗军译.北京:电子工业出版社，2013:6-7.

［2］朱江乐，章卫国，邱岳恒，等.基于改进证据理论的多传感器目标识别［J］.火力与指挥控制，2013，38（8）:107-110.

［3］王少蕾，陈维义.基于粒子群K均值聚类的空中目标识别［J］.舰船科学技术，2012，31（12）:30-34.

［4］Anagnostopoulos G C.SVM-based Target Recognition from Synthetic Aperture Radar Using Target Region Outline Descriptors［J］.NonlinerAnalysis，2009，71（12）:2934-2939.

［5］高晶，吕伟，陈游.基于关联离散度的目标类型识别方法［J］.火力与指挥控制，2012，37（1）:105-107.

［6］赵杰，林辉.基于BP神经网络模型的目标属性识别仿真［J］.系统仿真学报，2007，29（11）:2571-2573.

［7］周浩，韦道知，金凤杰.RBF神经网络在目标识别中的应用研究［J］.弹箭与制导学报，2008，27（5）:215-216.

［8］朱宁.基于多传感器信息融合的空中目标识别算法研究［D］.哈尔滨：哈尔滨工业大学，2008.

Target Recognition Based on RBF Neural Network

LIU Yan-ju，KOU Guo-hao，SONG Jian-hui
（School of Information Engineering Shenyang Ligong University，Shenyang 110159，China）

Air target‘s accurate identification directly affects the development of anti-aircraft fire allocation and effective combat.Radial basis function（RBF）neural network is adopted to approximate nonlinear air target identification model.In the air target recognition model based on RBF，six properties of air targets are extracted by radar as neural network input vector，and the type of flying target is taken as the output vector.Simulation results show that the error of RBF model is smaller in comparison with traditional BP neural network model by Matlab simulation，which effectively improves the recognition rate of air targets.

target recognition，RBF，radar，modeling and simulation

TP183

A

1002-0640（2015）08-0009-05

2014-07-05

2014-08-07

辽宁省教育厅科学技术基金资助项目（L2014079）

刘砚菊（1965-），女，教授，博士。研究方向：智能仪器与控制装置。