反舰导弹末制导雷达搜索范围优化模型

沈培志，张邦钰

（海军航空工程学院，山东烟台264001）

反舰导弹末制导雷达搜索范围优化模型

沈培志，张邦钰

（海军航空工程学院，山东烟台264001）

对反舰导弹末制导雷达搜索范围合理性的相关问题进行了分析，对两种描述搜索范围的模型进行了研究，并在此基础上提出了改进模型。通过计算机对3个模型分别进行了仿真，从捕捉概率对搜索范围大小的影响入手，对该问题进行了定量分析。得到了相同条件下捕捉概率随搜索范围变化而变化的仿真数据，通过数据对比验证了改进模型中搜索范围的合理性，为今后此类问题的研究提供参考和借鉴。

反舰导弹，末制导雷达，搜索范围，模型

0　引言

由于电子对抗手段的逐渐丰富，影响反舰导弹对预定目标捕捉的因素也越来越多。对于采用雷达末制导的反舰导弹而言，影响因素有导弹自控终点散布、目标散布、各类干扰手段、目标舰艇编队队形、岛岸回波等。在这样的条件下，要实现对预定目标的准确捕捉，不仅要求目标位于末制导雷达搜索范围内，还要求末制导雷达能够从可能存在的众多回波中将预定目标分辨出来。当末制导雷达的搜索范围越大时，预定目标位于该搜索范围内的概率就越大；但同时在末制导雷达接收到的回波中，非预定目标的回波可能就越多，这将增加末制导雷达的选择难度［1］。当搜索范围越小时，非预定目标的回波数量可能相对减少，但同时也降低了预定目标位于搜索范围内的概率。这就对末制导雷达搜索范围的确定提出了新的课题。通过上述分析可知，合理的搜索范围必须要满足两个基本条件：一是要使预定目标位于该搜索范围内，二是避免接收到过多的非预定目标回波。为此在研究末制导雷达搜索范围时，必须要将捕捉概率和搜索范围结合起来，找到满足上述两个条件的最小搜索范围。

1　搜索范围建模方法分析及改进

1.1等效圆形模型下的搜索范围

将导弹有效自控终点散布考虑为一个圆形且不考虑目标散布时［2］，末制导雷达搜索范围如图1（a）所示：

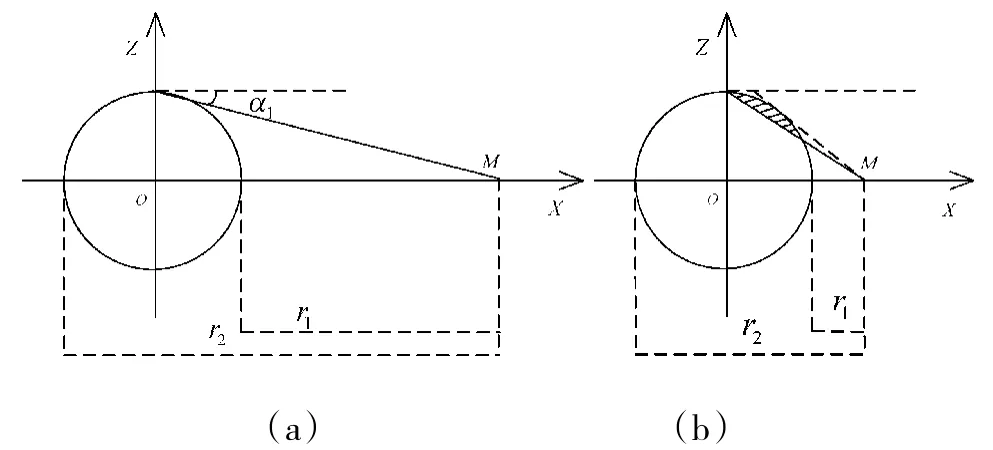
图1　等效圆形散布模型的搜索范围示意图

其中，X轴正方向为导弹飞行方向，圆O是导弹自控终点散布圆，M为目标位置点。由图中所示关系可知，要实现对目标的准确捕捉，就要求在自控终点横、纵向散布最大时，导弹末制导雷达能够确保对目标的照射。相关文献中一般按照导弹自控终点散布规律取得等效圆的散布半径，这就建立了捕捉概率与搜索范围的关系。

由此，在已知导弹自控终点散布圆半径r和开机距离dk的情况下，设末制导雷达角度搜索范围为2α1，则：

搜索远近距为：

在该模型中，若导弹散布范围过大或者自导距离较近，则会出现图1（b）所示情况：当导弹位于图中阴影部分时，目标将处于搜索范围以外，这表明等效圆形散布模型确定的搜索角度过小。由于等效圆模型描述了一定捕捉概率条件下末制导雷达的搜索范围，若搜索角度过小，会使得当前搜索范围的实际捕捉概率偏小，由此产生了模型描述的实际捕捉概率与预设捕捉概率不对应的情况，这与题设条件不符。

1.2等效矩形散布模型下的搜索范围

在文献［2］所提到的等效矩形散布模型中，将自控终点有效散布区域等效为圆形散布的外接矩形所包围的区域，设末制导雷达角度搜索范围为2α2，如图2所示。

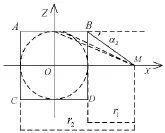
图2　等效矩形散布模型的搜索范围示意图

此时，搜索距离不变，搜索角度变为：

由图2容易知道，相比等效圆形而言，等效矩形散布模型确定的搜索角度过大。与等效圆模型类似，等效矩形模型所描述的捕捉概率与预设捕捉概率不符。

2　利用改进算法确定搜索范围

上述两种模型较为直观，计算较为简便，虽可以满足末制导雷达对目标的照射条件，反映一定的实际情况，但仍然存在3个缺点：一是在不同情况下不能完全描述实际的搜索范围情况，等效圆形模型确定的搜索角度过小，等效矩形模型确定的角度过大；二是当导弹横、纵向散布相差较大时，模型的计算精度较低，所得到的搜索范围不是最小的，与实际情况相差较大；三是难以确定导弹的散布圆半径，导致末制导雷达搜索范围难以与捕捉概率相结合而失去实际意义。

为满足题设中所提出的合理搜索区的两个条件，这里针对上述模型中存在的问题进行两点改进：一是将横纵散布分开处理；二是结合一定的概率确定最小散布范围。

结合等效圆形散布模型和等效矩形散布模型所描述的搜索范围，对文献［2］及其他文献提到的导弹自控终点散布模型进行如下改进。设导弹自控终点散布满足正态分布且两方向相互独立［3-4］，并分别从横侧向两个方面独立研究其散布问题，从而得出相应的搜索距离和角度。如图3所示。

图3　横纵向正态分布示意图

求导弹的搜索角度和距离，就必须找到导弹满足概率为p时的散布大小，并通过几何关系求出搜索范围的角度和远近距大小。

设导弹落在-a到a之间的概率为Pz，它们与捕捉角度的关系为：

同理可得在纵向上的散布概率与搜索距离的关系：

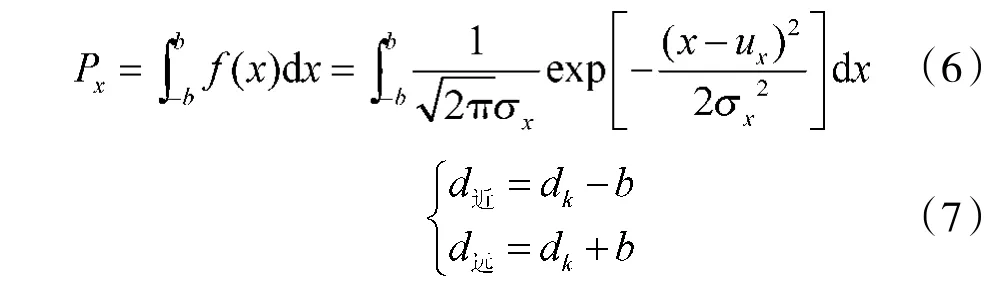
由于横纵向互相独立，导弹自控终点在散布区域（-a，a）及（-b，b）中的概率为：

3　仿真计算

为了方便本文中3个模型的对比，这里给出3个模型确定的搜索范围所覆盖的海区面积。由于各个搜索范围都可以看成圆环的一个部分，因此，覆盖面积均可通过下式求得：

首先对新算法进行多次计算，得出不同概率条件下搜索范围的角度和距离值。这里取开机距离dk=40 km，分别取导弹横、纵向散布误差的标准差为σz=3 km和σx=1 km。结果如表1所示：

表1　新算法下不同捕捉概率的搜索范围取值

当然横纵向散布误差的不同会使得搜索概率和范围的值发生变化。为了对比3个模型所描述的导弹搜索范围大小，这里利用正态分布的“3σ”法则［5］对等效圆形和等效矩形的散布半径进行取值。例如：根据“3σ”法则可知，在σ=3 km时，取9 km为其散布半径r，此时导弹自控终点落在该圆范围内的概率是99.74%。由此根据式（9），可得在捕捉概率为99.74%时，3个模型的搜索角度和距离以及搜索范围覆盖的海域面积如表2所示，这里取σz=σx为1 km，3 km，5 km［6］。

表23　个模型下的搜索范围对比（P=99.74%，σ=1 km）

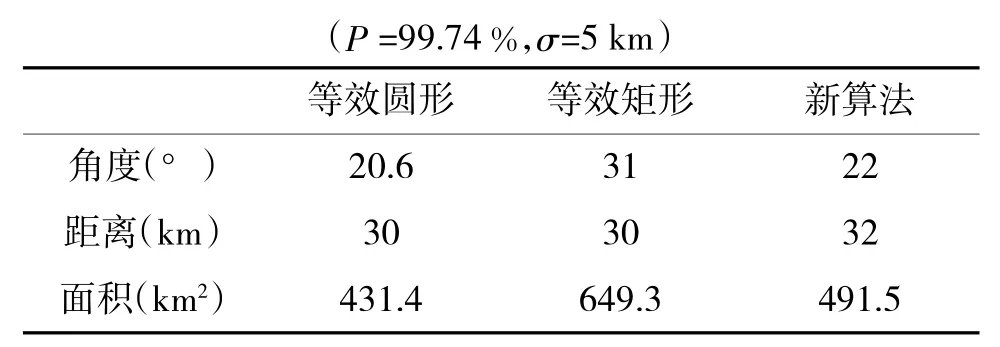
（P=99.74%，σ=5 km）等效圆形等效矩形新算法角度（°）20.63122距离（km）303032面积（km2）431.4649.3491.5

4　结论

通过建模和分析可以得出以下结论：

①在同等假设条件下，两种等效模型计算出的搜索范围存在偏大或偏小的问题，这与前面章节的分析结果相同，而新算法搜索范围适中，更符合实际情况。②末制导雷达搜索范围与捕捉概率关系密切，在同等条件下，搜索角度、搜索距离越大，捕捉概率就越大。③等效圆、矩形两个模型只能求出已知散布半径时的搜索范围；或者已知误差时，搜索概率为99.74%的搜索范围，而新模型可以得出满足一定概率时的角度和距离取值，为找到合理的搜索范围提供依据。④如表1所示，新模型还可以运用于横、纵散布差别较大的情况。

5　结束语

本文所提出的反舰导弹末制导雷达搜索范围优化模型，可以较为准确地描述反舰导弹目标捕捉概率与末制导雷达搜索范围的关系，贴合了实际情况。该模型建模过程简单，易于理解，计算结果也更为合理，从一定程度上避免等效圆形和等效矩形模型出现的搜索区偏大或偏小问题，可以为反舰导弹末制导雷达搜索范围的确定提供依据。

［1］卢毅，姜永华，范照盛.一种基于点集匹配的反舰导弹目标选择方法［J］.宇航学报，2011，17（9）：2037-2044.

［2］卢毅，姜永华，翟龙军.末制导雷达一次捕捉最小角度搜索范围模型［J］.宇航学报，2011，17（3）：599-602.

［3］高晓冬，王光辉，李传顺.一种改进的反舰导弹前置点射击方式目标捕捉概率算法［J］.海军航空工程学院学报，2012，22（2）：228-230.

［4］卢燕，舒传模.蒙特卡洛法在导弹末制导雷达对目标的位置捕获概率估计中的应用［J］.战术导弹技术，2005，19（6）：55-58.

［5］盛骤，谢式千，潘承毅.概率论与数理统计［M］.北京：高等教育出版社，2001.

［6］张邦钰，沈培志.一种反舰导弹目标捕捉概率计算模型的改进［J］.四川兵工学报，2015，34（3）：20-22.

Model on Searching Angle of Anti-ship Missile Terminal Guidance Radar

SHEN Pei-zhi，ZHANG Bang-yu
（Naval Aeronautical and Astronautical University，Yantai 264001，China）

Based on the analysis of rationality about searching angle of terminal guidance radar of anti-ship missile and the research of two models which have described the relationship of searching angle，this thesis puts forward an improved model.Starting from the influence of acquiring probability on searching angle，with quantitative analysis，the problem has been worked out by the results of computer simulations of three models.It has got the data that acquiring probability follows searching angle.By comparison，the rationality of searching angle in the improved model has been proved.It provides reference to future similar studies.

anti-ship missile，terminal guidance radar，searching angle，models

TN97；TJ761.1+4

A

1002-0640（2015）08-0078-03

2014-07-25

2014-08-17

沈培志（1972-），男，山东龙口人，副教授。研究方向：武器效能评估与运用。