电学中的对称美及其在高职电工基础教学中的运用

徐 茜

（深圳职业技术学院，广东 深圳 518055）

科学的本质是“真、善、美”，这种科学美，历来为科学大师所推崇，法国数学家亨利·庞加莱（Jules Henri Poincaré，1854-1912）曾说：“一个名符其实的科学家，尤其是数学家，他在自己的工作中体验到和艺术家一样的印象。他的乐趣和艺术家的乐趣具有同样的性质，是同样伟大的东西。”[1]这种科学美在电工基础理论中也有明显表现，电工基础理论所揭示的真理是真与美的统一。对称美是电工基础理论中常见的美学的特征，分析和探讨电工基础理论的对称美学特征，并把它应用到高职教学中，对于改进教学，提高学生的学习兴趣，拓宽思路改善思维方式有重要作用。

1 电工基础理论中的对称美

对称（偶）性普遍存在于宇宙之中，在日常生活中处处都可见到对称，洁白的雪花，彩色的蝴蝶，绚丽的花瓣等无不呈现出妙趣天成的对称性。人们对于对称性美的体验，来自对于人体、动物、植物、山川、河流等外形美的观感上，自然美的外观表现是自然美的形式美。在中国的国粹文化中，对称美具有独特的地位，中国的建筑、绘画、诗歌、楹联、图章、书法等，都闪耀着对称美的光辉。对称性的美学价值是一个神秘而有趣的现象。

电路是由电气器件相互连接而构成的，具有传输电能、处理信号、测量、控制等功能。我们知道，分析集总参数电路，主要是基于两类约束方程的求解，一类是元件约束方程，一类是电路结构约束方程（或拓扑约束方程）。元件约束是构成电路的每个元件上的电压电流关系或称伏安特性，如线性电阻元件，其元件约束满足欧姆定律 u=Ri；结构约束是电路的连接关系确定后，各元件的电流之间或电压之间受到的约束关系，表示这类约束关系的是基尔霍夫定律，它只与电路的拓扑结构有关，即对任意一个结点，与结点关联的支路电流满足基尔霍夫电流定律 ∑i=0，对任意回路，与回路关联的各部分电压满足基尔霍夫电压定律 ∑u=0。

在电路分析中，我们会发现一个有趣的现象，一些电路变量、元器件、电路结构乃至电路定律定理等会成对出现，其间会存在明显的一一对应关系，这种特性称为电路的对称（偶）性。比如电压u和电流i、电阻R和电导G、感抗和容抗、阻抗Z和导纳Y、电感L与电容C、电压源和电流源、VCCS和CCVS、VCVS和CCCS、网孔（回路）和结点、串联和并联、开路和短路、分压和分流、基尔霍夫电流定律和电压定律、戴维南定理和诺顿定理等等。显然，线性电阻的伏安关系为u=Ri，线性电导的伏安关系为i=Gu，两个关系式中，如果u和i、R和G互换，则两个关系式可以互相转换。同样的，基尔霍夫电流定律表述为：对任意结点，有约束关系∑i=0，基尔霍夫电压定律表述为：对任意回路（网孔），有约束关系 ∑u=0，如果结点和回路、i和 u互换，则两个约束关系也可以互换。由于电路分析的两类约束关系均存在这种互换性，可以推论，电路分析中，由这两类约束关系推导得到的电路定理、电路分析方法等也存在这种互换性。上述具有这种一一对应关系，可以互换的元素称为对偶元素。

电路中某些元素之间的关系（或方程），用他们的对偶元素对应地置换后，所得到的新关系（或方程）也一定成立，这个新关系（或方程）与原有的关系（或方程）互为对偶，这就是电路中有着美学特性的重要理论对偶原理[2]。

2 教学实践中对称美学的运用

高等职业技术院校各专业电工课程，并未将电路理论的对偶原理纳入课程教学大纲，但这并不影响我们在教学过程中，很自然地引入哲学和美学范畴的“对偶（称）”概念，它本身是一种自然的属性，比如：远近、高低、圆缺、胖瘦、大小、东西、男女、美丑、开关、增减、升降、上下、阴阳等等，对偶（称）现象无处不在，而且因为形成对偶的两个元素之间对比强烈，给大脑留下深刻印记，对偶在中国诗文中，常表现为对仗为大众喜爱。

首先，通过引入对偶概念，加深对一些抽象电路概念的理解记忆。电路中，用足以反映其电磁特性的理想元件及其组合来模拟实际电路中的器件，即电路模型，其中，电阻R、电感L、电容C和电压源模型的概念相对容易接受，而电流源是一个新的概念，因为生活中无从体验，所以显得更抽象。我们可以从相对熟悉的电感元件L和电容元件C引出对偶概念，L和C一个储存磁场能，一个储存电场能，磁场和电场是一对对偶量，L和C是一对对偶元件，进而提出，电压源和电流源也存在对偶关系，电压和电流也是对偶量。我们发现，对偶概念不仅反映在电路元件对偶（对偶元件）、电路结构对偶、电路特性对偶，也反映在电路定律和定理中，它是电路中普遍存在的现象。借助对偶概念，我们可以很自然地引入与电阻R对偶的一个电路元件电导G，以及欧姆定律对偶形式u=Ri和 i=Gu，发现基尔霍夫电压定律和电流定律是一个对偶的结论∑i=0和∑u=0。

在电工教学中，我们一开始就自然引入对偶概念，不仅能加强对抽象概念的记忆，同时也能从宏观上把握电路的规律性，让初学者赏心悦目，感受到电学之美，激发学生学习兴趣。电路中常见对偶元素见表1。

其次，在电路分析中不断强化应用电学美学特性。如图1所示，电阻的串、并联电路，分析图1（a）电路，得到，等效电阻 R=R1+R2，分压公式：对于图1（b）电路，只要分析说明它与图1(a) 的对称（偶）关系，电路结构对称：并联对串联；电路变量对称：电流对电压；电路功能对称：分流对分压；电路元件的对称：电导对电阻。并联电路中的电阻常用电导参数表示，即G1=1/R1，G2=1/R2 ，这样做的理由，仅仅是为了让两个电路完全对称起来。于是得到图1（b）电路等效电导G=G1+G2，分流公式：

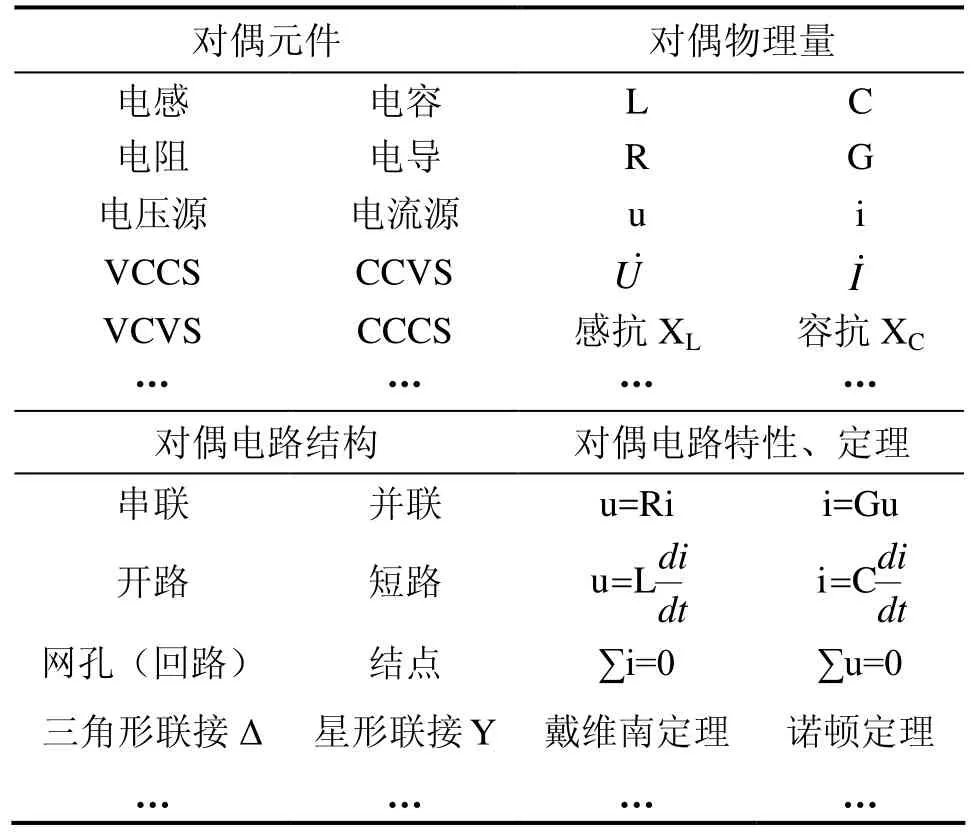
表1 电路常见对偶元素一览

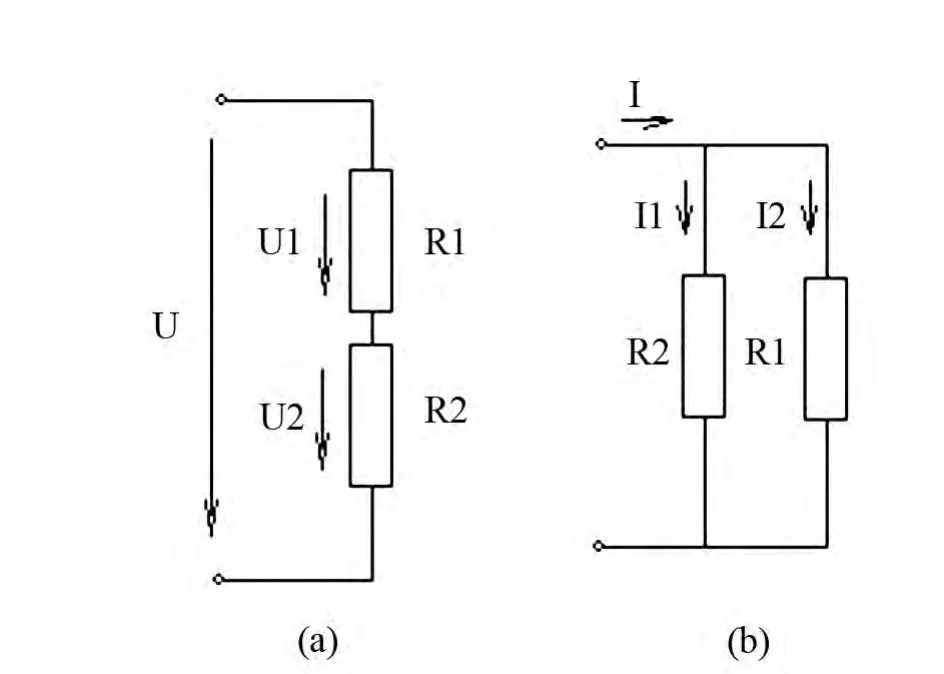
图1 电阻串、并联电路

这里，重点是对电路对称（偶）特性的认识，方便记忆分压分流公式，而且，这个结论可以推广至n个电阻（导）串（并）联的情况。

另外，借助电路对称（偶）性特性，可以加深对电路抽象概念的理解。例如，电路模型中，有理想电压源，自然就会有理想电流源。一个实际电源，可以用理想电压源和一个电阻串联来表示，与之对应，一个实际电源也可以用一个理想电流源和一个电导并联来表示，这样，可以自然而然地引出实际电源的两种电源模型等等。在教学中，不断地发现、认识、应用电路的对称（偶）性、统一性等美学特性，达到事半功倍的效果。

3 几点讨论

3.1 从美学的观点考察电学有利于思维方式的多样化

现代科学是以概念为中心依靠逻辑推理建立起来的理论体系，电学也不例外，通过这套体系的严格逻辑性保证了电学的可靠性。但从美学的观点考察电学，提供另外一个相对直观的思维方式与观察方法，有利于促进研究和教学的多样化。

就电学中的对称美来说，对偶原理的本质是电路中对应的对偶元素互换后，相应的数学方程（模型）是不变的，所以方程的解不变。它是电网络理论中重要的电路定理。教学实践中，我们更注重其在思维方法上的指导作用。通过对电路对偶元素的认识，运用对偶关系，使学生对基本概念、电路分析方法、电路定律、电路定理有更好的理解，记忆更牢固。在教学中，启发学生善于比较分析，及时总结发现规律性的东西。

3.2 电工中的美学概念尚有许多可以深挖之处

除了对称美的现象与概念之外，电学还有许多美学现象与概念可以进一步研究和探讨。和谐统一性美就是一个例子。和谐是事物在矛盾对立的诸多因素相互作用下实现的统一。人的和谐感觉是与自然的和谐规律相统一的，它是一个合理的自然的运作规律。和谐统一是指由于相互之间恰到好处在整体上呈现出的协调，给人以统一、自洽、对应的美感。电学中的和谐美主要体现在电工理论形式与内容的统一、电路定律形式简单、内涵丰富、和谐统一。形式的统一性，就是美的事物在外在形式所具有的相对独立的审美特性。

直流电路中，元件约束方程的形式，即欧姆定律U=RI（直流电路中，电感L、电容C分别视为短路和开路）；电路拓扑约束方程的形式，即基尔霍夫电流定律和电压定律：∑I=0（对任意结点），∑U=0（对任意回路）。电路分析实际上是一组线性代数方程的求解。

正弦交流稳态电路中，电感L、电容C不再被视为短路和开路，和电阻R类似，L、C在电路中对电流也有“阻碍”作用，很显然这种“阻碍”作用的特性与电阻R是不一样的。时域中，对电阻R，其元件约束方程依然是欧姆定律u=Ri，对电感L，其元件约束方程为对电容C，其元件约束方程为电路拓扑约束方程依然是基尔霍夫定律 ∑i=0 （对结点）和∑u=0 （对回路），因此，正弦稳态电路分析实际上是常系数n阶微分（积分）方程的求解（其特解）。微分方程的求解比线性代数方程组求解繁杂得多，为此，正弦稳态电路的分析常用相量法。相量法本质上是一种数学变换，通过变换，建立时域的正弦量与相量域的相量的对应关系。我们发现，应用相量法，正弦稳态电路两类约束方程在形式上与直流电路是相似的：元件约束方程I&Z （对电阻Z=R，对电感Z=jwL，对电容称为相量形式欧姆定律；同样地，电路拓扑约束方程：∑I=0（对结点），∑0=（对回路），称为相量形式基尔霍夫定律。两类约束方程形式上的高度统一性，使得用相量法分析正弦稳态电路时，直流电路中的所有分析方法、电路定理等可以直接引用。这充分展现了电工理论简洁、和谐统一之美。

3.3 从美学视角认识、学习电工理论知识是提高学生学习兴趣有效方法

爱因斯坦说过：“兴趣是最好的老师。教育应当使所提供的东西让学生作为一种宝贵的礼物来接受，而不是作为一种艰苦的任务要他去负担。”电工基础课程的学习，对高职学生来讲普遍存在一定的困难：概念抽象、理论性强。因此，从探讨电工理论中的美学概念入手，为学生提供一种相对直观的思维方式和方法，善于引导学生去发现、认识电路的对称（偶）性、统一性，把它和生活中的审美结合起来，对于激发学生的学习兴趣提高学习效果极为有效。从第一堂课开始，就引入电路对称（偶）性概念，目的不是介绍一个电路定理，而是一个认知的过程，从元件、结构、现象、功能等的对称（偶）性，进而到电路公式、电路定理的对称性，学习的过程变得有趣、生动，公式和定理不再只是死记硬背。

[1] 徐本治．数学中的美学方法[M]．大连：大连理工大学出版社，2008．

[2] 邱关源．电路（第四版）[M]．北京：高等教育出版社，1999．

[3] 杨红，徐茜．电工及电气测量技术[M]．北京：机械工业出版社，2013．