基于XFEM法的拉壳钩裂纹扩展分析研究
2015-11-27吴宝双
刘 杭,李 强,吴宝双
(中北大学 机电工程学院,山西 太原 030051)
随着自动武器的发展,为了满足其高射速等一系列战技指标,部分构件几何尺寸日益极端化,作业环境复杂化,其中一个体现就是在自动武器射击过程中,由于拉壳钩反复抽壳,受到较大循环载荷作用,以及材料本身可能存在的缺陷,最终导致拉壳钩失效甚至断裂。产生这类事故的根本原因在于金属疲劳引起裂纹的产生,当裂纹发展到一定程度的时候,构件断裂。因此研究裂纹及其在一定程度下的扩展行为对提高武器可靠性意义重大。
目前,对于裂纹生成和扩展的研究已经有了很多成果,研究手段基本上分为两种:试验与统计相结合的方法和以断裂力学为基础进行数值分析的方法。随着计算机技术的不断发展,越来越多的学者开始采用数值分析的方法,但是传统的有限元分析方法在建模方面比较困难且数学表达式相对繁琐,因此不容易被广泛使用。扩展有限元法(以下简称XFEM)是在传统有限元法基础之上发展起来的一种新型的裂纹计算方法,应用XFEM 方法简化模型建模,不需要再对裂纹几何进行网格划分,提高计算精度,裂纹可以在单元边的内部通过[1]。
笔者以有限元分析软件ABAQUS为平台,运用XFEM 法对拉壳钩的裂纹生成扩展进行分析。
1 三维模型的建立
拉壳钩作为自动机的一部分,需要在射击之后及时将弹壳抽出。由于自动武器射速较高,抽壳阻力往往较大,对于小口径自动武器而言,抽壳阻力大约为几百牛顿[2]。而从总体设计的角度,为了实现减小质量等目的,拉壳钩往往都比较薄,因此在多次射击后,容易出现拉壳钩断裂的现象。拉壳钩三维模型如图1所示。

由于拉壳钩的三维模型比较复杂,而有限元分析软件ABAQUS的仿真精度严重依赖于网格的划分,采用实际模型很难划分出高质量的网格,不利于得到精确的分析结果。因此,在尽可能保证仿真精度的情况下对原模型进行了简化,忽略对结果影响不大的复杂结构,保留抽壳部分原有尺寸。
2 理论分析与计算
在该问题中关注的是Ⅰ型应力强度因子K1和J积分两个物理量,裂纹尖端的应力和应变具有高梯度性质,实际上具有奇异性。常规的做法是在裂纹尖端划分很细的单元,但即使这样也较难获得满意的结果;另一种方法是采用奇异单元,对于线弹性问题,位移在裂纹尖端具有阶奇异性,而应力具有1/阶奇异性,则可以采用具有奇异性的单元。由奇异性原理,对于平面8节点二次单元,有它的物理坐标(x,y)及基准坐标(ξ,η),设它们的坐标变换为

式中:ξ和η分别为基准体系下的横、纵坐标;x和y分别为横、纵物理坐标;N为基准坐标和物理坐标之间的转化函数。其中

对于8节点二次单元,如图2所示。

选择1-2边,涉及节点1,2,5,有

因此,
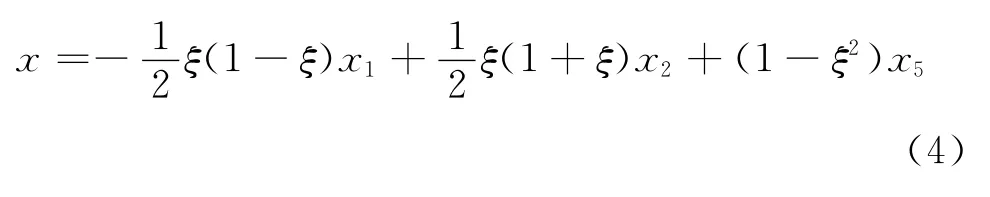
选择x1=0,x2=L,x5=L/4,则有

计算得到

沿1-2线,由等参元的位移
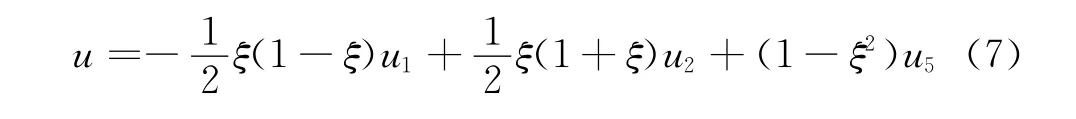
将ξ换为x有
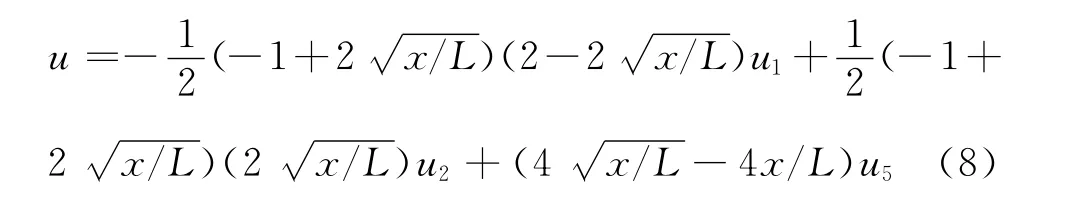
沿x方向上的应变为
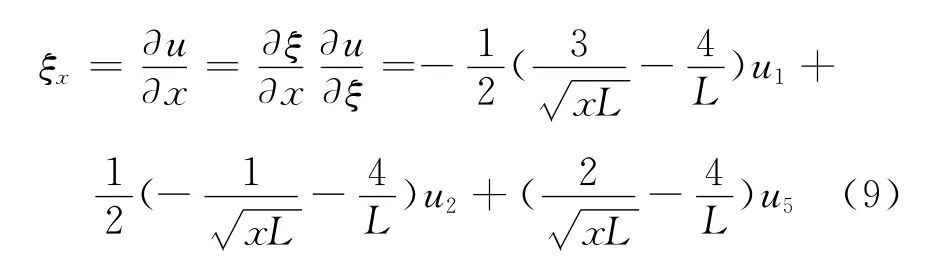
可以看出在1点(x=0)或(ξ=-1)处,应变具有1/阶奇异性。因此,由应变获得应力也具有相同的奇异性。
取θ=±180°,并忽略高阶项,由位移分布可以推导出如下的应力强度因子表达式:

当r→0时,设=A,则Ⅰ型应力强度因子K1=,其他两种应力强度因子求解方法类似。此外,也可以通过求解无限大板中周期排列的裂纹阵问题得到各型应力强度因子[3]。其中Ⅰ型应力强度因子K1的计算公式如下:
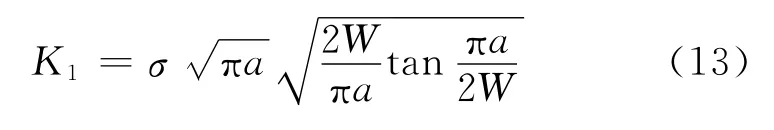
式中:a为裂纹半长,mm;W为裂纹所处圆弧面宽度,mm;σ为拉伸应力,MPa。
当a/W→0时,上式中应力强度因子的理论值趋于无限大裂纹板时的值,即K1→σ;当a/W→1时,K1→∞。经过数学证明[4],对于各向同性的均匀线弹性材料而言,J积分、应力强度因子K1有如下关系:

对于平面应力状态,=E;对于平面应变状态,=E/(1-υ2),E和υ分别为弹性模量和泊松比。
如计算参数为a=0.5mm,W=20mm,σ=192 MPa,则由以式(13)、(14)可解得

另外,为了验证仿真模型的可靠性,抽壳阻力F和裂纹尖端应力σ也是需要考察的对象。
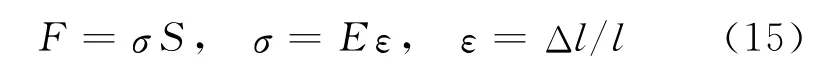
式中:S为抽壳面面积;ε为抽壳钩应变;Δl为抽壳钩轴向拉伸量;l为抽壳钩原长。取S=11.47mm2,Δl=0.01mm,l=50mm,可算得F=481.74N。
3 仿真分析研究
整个仿真过程思路为:先通过抽壳仿真,确定抽壳钩应力集中区域,再在应力集中区施加预裂纹,通过施加循环载荷,观察裂纹扩展情况,在此过程中输出应力强度因子和J积分。使用XFEM 方法计算J积分和应力强度因子K有两个条件:必须是静态裂纹,且必须是三维模型。在前处理中的设置是:首先在interaction模块中创建裂纹,并不允许扩展;在step模块的历程变量输出Domain中选择裂纹,Type选择J积分或者应力强度因子[5]。另外,分析步采用的是直接循环,打开疲劳分析并对疲劳分析和增量步进行一定设置。在场输出中需要设置PHILSM 和STATUSXFEM,分别用于查看裂纹等值面和扩展有限元单元状态。
3.1 有限元模型的处理
三维模型导入到ABAQUS 中进行有限元分析,长度单位选择mm,应力单位为MPa。抽壳钩材料参数选取如下,弹性模量E=2.1×105MPa,泊松比υ=0.3。本文采用的是基于损伤力学演化的失效准则,具体的参数设置如下:损伤判据为最大主应力失效准则作为损伤起始的判据,最大主应力为150 MPa。损伤演化选取基于能量的、线性软化的、混合模式的指数损伤演化规律,有关参数为G1=G2=G3=42.2kN/m,α=1。
3.2 拉壳钩仿真边界条件
由于施加了循环载荷,因此选用直接循环的分析步,为了有利于收敛,如前文所述,将原有分析结果中拉壳钩所受载荷转化为位移,拉壳钩底部完全约束,采用约束方程将弹底与拉壳钩的接触面同样约束起来,另外,在拉壳钩受边界条件约束的位置添加一个参考点,方便输出反力,此处等效为抽壳阻力。由于是塑性变形,对抽壳钩受力部位选择C3D8I单元,其余部分采用自由网格。建立的仿真模型如图3所示。

3.3 仿真结果
对于裂纹扩展而言,调整时间增量步长很重要,增量步太大容易在一个步长内裂纹扩展过大,难以看清裂纹尖端发展过程,增量步太小又太耗费计算时间,因此增量步需要多次调试之后才能确定。图4为裂纹扩展过程。
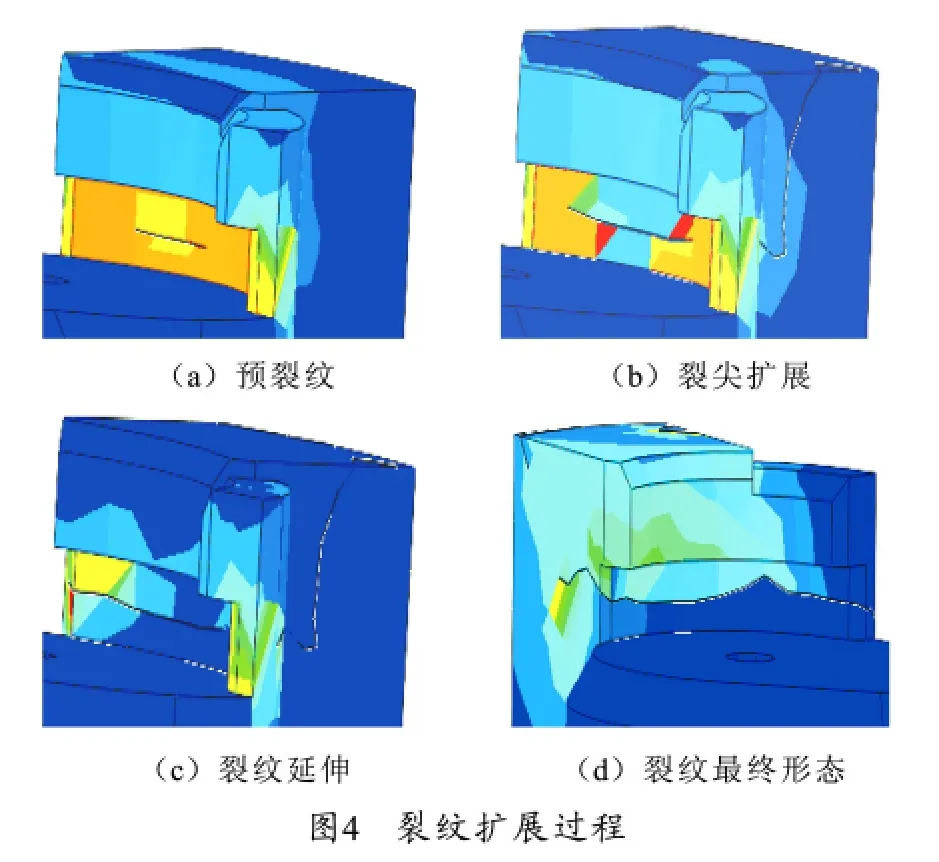
3.3.1 裂纹扩展过程分析
从上述的裂纹扩展过程的应力分布图,可以得到如下几点结论:在裂纹尖端出现了应力集中,这是和断裂力学理论符合的;裂纹的产生位置和扩展过程与实际过程中的情况基本一致[6],这证明了数值模拟裂纹扩展是可靠的。
3.3.2 裂纹尖端应力和J积分仿真结果分析
仿真过程中,设置拉壳钩上编号为9792 号单元为一个集合,用来输出裂纹尖端应力的变化规律。裂纹尖端应力变化规律如图5所示。

由图5可以大致得到这个裂尖单元参与断裂过程的整个历程。在应力加载之初,裂尖单元的应力随着载荷的增加而增加,应力线性增长。这是由于此时裂尖单元的应力并没有达到损伤判断的临界应力,从宏观上看,处于材料变形的弹性阶段,因此单元没有起裂。随着载荷的持续增加,应力值也继续增加,在0.156s左右时,裂尖的最大主应力达到了最大主应力损伤判断的临界值,于是开始起裂,直至完全裂开,单元的应力奇异性消失,裂尖单元转变为一个普通的非裂尖单元。这个过程体现在图中0.156-0.156 5s应力增大后又急剧减小,之后,由于载荷还没有完全加载完毕,所以裂尖单元在转变为普通单元之后,应力虽然减小但并未消失,分析步结束时,残余应力约为75 MPa。
事实上,裂纹尖端应力只是为了方便理解裂尖单元从起裂到完全断裂的整个过程中的行为。在裂纹扩展过程中对断裂韧强度的定量研究需要的是应力强度因子和J积分,拉壳钩裂纹扩展过程中J积分的变化如图6所示。

从图6可以看出,分析步结束时J积分为275 N/m,上文中在完全施加载荷条件下的理论计算值为278N/m,仿真结果与理论计算值基本吻合。
3.3.3 抽壳阻力仿真结果分析
由于拉壳钩根部直接将弹壳抽出,因此将拉壳钩上预定点的反作用力等效为抽壳阻力。对抽壳阻力的分析有助于验证有限元模型的可靠性。结点反力变化如图7所示。

从图7可以看出,0-0.156s结点反力线性增加,在0.156s时反力出现急剧减小,值得注意的是,裂尖单元应力在此时也出现了阶跃,这是因为裂纹扩展变长,承受载荷的截面积变小,承载能力下降。从图中可以看出裂纹是突然扩展的,因此力的下降非常迅速,出现阶跃。在此之后直到分析步结束,反力又逐渐增大,最终反力为-485N,这与上文中计算出来的481.74N 基本相符,也与试验数据吻合得很好[7],说明有限元分析结果是可信的。
至此,对于仿真模型拉壳钩中裂纹产生和扩展有了进一步的认识:拉壳钩抽壳的时候受到较大的抽壳阻力,在构件薄弱的地方形成应力集中区域。又由于抽壳阻力是一个循环载荷,如果材料本身也有缺陷就可能形成裂纹。随着载荷的不断增大,裂尖处的单元应力也不断增加。当裂尖处的最大主应力值达到临界值时,裂尖处的单元开始失效,裂纹开始穿过单元扩展,在0.156s左右,裂尖处开始形成黏结裂纹。0-0.156s这个过程可以认为是裂纹孕育期。之后随着裂尖处的能量释放率达到裂纹扩展阻力率时,裂尖处的黏结裂纹开始扩展成真实裂纹,裂尖处的单元损伤值达到临界值,此时可以认为局部结构开始失效。此后,裂纹失去平衡,开始失稳扩展,0.156-0.2s真实裂纹开始形成并不断扩展。
4 结论
拉壳钩断裂在自动武器射击中时有出现,但是对于其裂纹的扩展缺乏定量的研究,以此为出发点,运用有限元软件ABAQUS 的XFEM 法,模拟裂纹扩展过程,得到了裂纹尖端应力变化规律和J积分变化规律并对仿真结果进行了理论评估。此外,将拉壳钩上的反力等效为抽壳阻力,仿真得到的抽壳阻力为485N,与试验结果吻合度较高,该仿真分析得出的数值与理论计算值对比说明XFEM法对于裂纹扩展分析可靠度很高,从而为定量研究裂纹生成过程提供了一种新方法。本文仿真基本参数源于小口径自动武器,基于同样的原理,本文中部分仿真结果对小口径武器拉壳钩的优化设计和大口径火炮抽筒子裂纹分析同样具有参考价值。
(References)
[1]张永涛,戴劲松.王茂森,等.某自动机身管衬套断裂分析[J].火炮发射与控制学报,2011(3):67-70.ZHANG Yongtao,DAI Jinsong,WANG Maoseng,et al.Study on fracture of barrel bushing of automatic mechanism[J].Journal of Gun Launch &Control,2011(3):67-70.(in Chinese)
[2]方修君,金峰,王进廷.基于扩展有限元法的粘聚裂纹模型[J].清华大学学报:自然科学版,2007,47(3):344-347.FANG Xiujun,JIN Feng,WANG Jinting.Cohesive crack model based on extended finite element method[J].Journal of Tsinghua University:Natural Science Edition,2007,47(3):344-347.(in Chinese)
[3]薄玉成,王惠源.自动机结构设计[M].北京:兵器工业出版社,2009:167-174.BO Yucheng,WANG Huiyuan.Automatic machine structure design[M].Beijing:The Publishing House of Ordnance Industry,2009:167-174.(in Chinese)
[4]杨继运,张行,张珉.基于疲劳裂纹形成曲线的裂纹扩展分析 数 值 方 法[J].机 械 工 程 学 报,2004,40(7):55-62.YANG Jiyun,ZHANG Xing,ZHANG Min.Numerical method for crack extension analysis based on fatigue crack formation curve[J].Journal of Mechanical Engineering,2004,40(7):55-62.(in Chinese)
[5]方修君,金峰.基于ABAQUS 平台的扩展有限元法[J].工程力学,2007(7):6-10.FANG Xiujun,JIN Feng.Extended finite element method based on ABAQUS[J].Engineering Mechanics,2007(7):6-10.(in Chinese)
[6]解德,钱勤,李长安.断裂力学中的数值计算方法及工程应用[M].北京:科学出版社,2009:167-174.XIE De,QIAN Qin,LI Chang’an.Method and application of numerical calculation in fracture mechanics[M].Beijing:Science Press,2009:167-174.(in Chinese)
[7]ANDERSON T L.Fracture mechanics:fundamentals and applications[M].2nd ed.Boca Raton:CRC,1995.
