基于切削颤振抑制系统的BP神经网络PID控制研究

张道坤，霍睿，王志东

(1.山东大学机械工程学院，山东济南250061;2.山东大学高效洁净机械制造教育部重点实验室，山东济南250061)

0 前言

对于金属切削过程中的自激颤振的控制，传统上主要是通过合理设计和优化系统参数，或应用被动消振装置来降低系统振动能量，近年来基于主动振动控制技术而发展起来的机床切削颤振在线监测与控制技术受到了较多的重视。主动控制方式的优点主要在于，可以克服切削系统和切削过程的时变性给被动控制的设计带来的困难;然而由于切削颤振抑制系统具有明显的非线性特征，经典的线性系统控制理论难以取得理想的控制效果。

目前BP神经网络已经成为目前应用最广泛的神经网络模型之一，其突出的特点是具有很强的非线性映射能力和柔性的网络结构。BP神经网络PID控制不但继承了经典PID控制的鲁棒性强、可靠性强和算法简单的优点，又整合了BP神经网络的非线性逼近和预测能力以及在线优化等特点，为机械加工朝着高精度、高效率和智能化方向迈进提供了新的思路和途径。

1 分布参数压电智能切削颤振抑制系统动力学模型

传统的切削颤振的发生机制分析一般基于单自由度集中参数模型，但不适用于具有明显分布质量特征的系统，例如镗削。图1是根据压电智能结构振动主动控制思想构造的压电智能镗杆，对称粘贴在镗杆上下表面的两片压电片，其一作为传感器，另一片作为执行器;传感器的输出电压us通过控制器算法转换为执行器的输入电压uc，导致执行器产生控制力矩来抑制镗杆颤振。

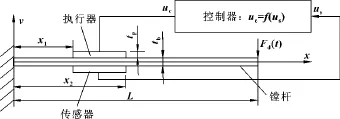
图1 压电智能镗杆的动力学模型

压电智能镗杆的弯曲振动的微分方程为

式中:w(x，t)为梁的横向位移;E、ρ、c分别为梁的杨氏模量、密度和阻尼;A(x)为梁的横截面积;I(x)为梁的截面惯性矩;Mp(x，t)为压电作动器产生的控制力矩;Fd(t)为作用在镗杆末端的动态颤振力。式 (1)中，在镗杆末端作用有颤振动态切削力表达为

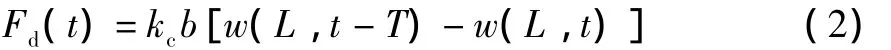
式中:kc、b分别为切削刚度和切削宽度，T为工件旋转周期。

压电作动器产生的控制力矩与其控制电压uc成正比例关系

式中:K＝0.5EpB(tb＋tp)d31，Ep、d31分别为压电片的弹性模量和电荷压电常数;B为压电片的宽度;tb、tp分别为基梁和压电片的厚度;H(x)是Heaviside函数;x1、x2是压电片两端点位置的横坐标;us是压电传感器的输出电压，且

式中:Cs为压电片电容。

根据振型叠加原理，在式 (1)中令

式中:Yi(x)和 φi(t)(i＝1，2，…)分别为镗杆(压电悬臂梁)的振型函数和模态坐标。

将式 (2)、(3)、(5)代入式 (1)，并利用振型函数的正交性，可得

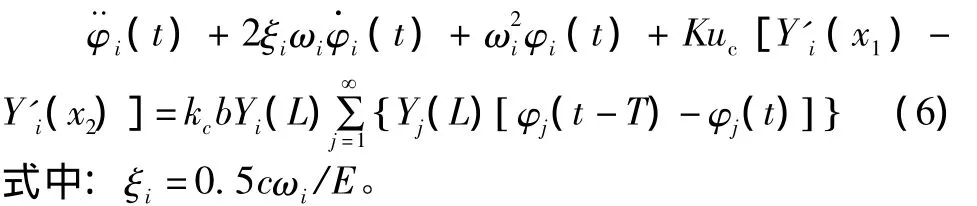
设若取前N阶模态进行分析，定义系统状态变量

式中:A、B、C、D分别为状态矩阵、延时矩阵、控制矩阵、输出矩阵，且有

2 基于BP神经网络PID控制策略的压电智能镗杆系统动力学仿真

2.1 BP神经网络PID控制器结构

图2为BP神经网络PID控制器应用于压电智能镗杆系统的控制原理，整个控制器包含经典PID控制器和BP神经网络两个组成部分。PID控制器以控制指令与压电传感器的反馈电压us的比较作为输入，其输出即作为压电执行器的控制电压uc;PID控制器的3个参数kP、kI、kD为在线调整参数，由BP神经网络通过加权系数的不断调整，根据系统当前状态进行实时调节，以达到设定性能指标的最优化。

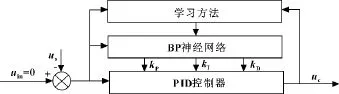
图2 BP神经网络PID控制器

控制器参数设置:综合考虑计算量和精度，采用三层BP神经网络结构，输入层选择4个节点，按照常规经验，隐含层取5个节点，输出层3个节点分别对应于PID控制器的3个参数kP、kI、kD。网络权值的初始值取 (-1，1)之间的随机实数，权值系数的修正采用梯度最速下降法;网络学习速率η＝0.25，惯性系数 γ ＝0.05。

2.2 颤振抑制系统参数设置

在整个切削颤振抑制系统中，是通过输出电压值的大小来反映振动抑制的效果。不过从状态方程可以看出，颤振系统的输出电压和一阶和二阶的振动位移是成正比的，当两者的振动位移减小后，输出电压自然减小了，因此在此仿真中通过跟踪振动位移的变化来探讨颤振抑制的效果。又因为一阶和二阶的控制方式是相同的，因此文中仿真只针对一阶来进行。

2.3 基于BP神经网络PID控制的切削颤振抑制系统仿真

为了说明BP神经网络PID控制在颤振抑制系统应用中的有效性，分别采用经典PID控制与BP神经网络控制对颤振抑制系统进行仿真分析，并对仿真结果进行了系统的比较分析。

2.3.1 经典PID控制仿真

图3为比例、积分和微分环节的参数模型图。按图在Simulink中进行模型的搭建和仿真，得出图4和图5的控制前后振幅图。

图3 比例、积分和微分环节模型图

图4 未加控制振幅图

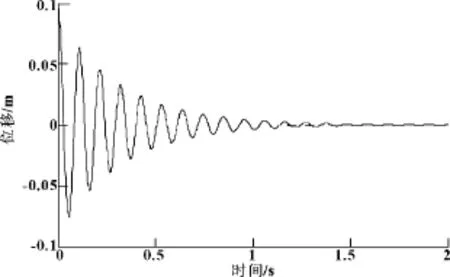
图5 PID控制振幅图

图4 为未施加控制前的系统颤振振幅图，图5为进过经典PID控制后的振幅图，其中PID的各个控制参数是由经验而得。对比两图可以看出，经典PID控制也能有效的对颤振系统进行控制。只要选择合适的比列、积分和微分参数，颤振系统能够在较短的时间能趋于稳定。

2.3.2 BP神经网络PID控制仿真

利用前述的理论知识，结合表1基体梁和压电片的参数，求出切削颤振抑制系统的动力学模型。并根据前述的BP神经网络PID控制器参数及其采用的算法，在Simulink中完成模型的搭建与仿真，如图6所示。

图6 Simulink仿真模块图

表1 梁和压电片的尺寸及性能参数

图7为控制振幅图，分析发现系统的振幅随着参数的不断修正，振动幅度越来越小，并达到稳定状态，可见BP神经网络PID控制系统能很好地控制颤振抑制系统。图8为控制系统中比例、微分和积分的参数调整图，3个值在开始阶段都呈震荡变化，但是随着系统振动曲线逐渐收敛到平衡位置。

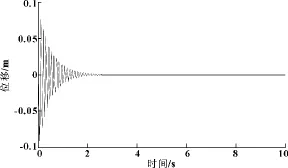
图7 BP神经网络PID控制振幅图

图8 BP神经网络PID控制参数调整图

2.3.3 经典PID控制与BP神经网络PID控制仿真对比

2种控制的各个参数不发生改变，通过改变模型的转速，分别采用上述的2种控制方法进行仿真，得到如图9和图10系统控制仿真图。

图9 经典PID控制振幅图

图10 BP神经网络PID控制振幅图

经典PID控制只能对具有固定参数的系统进行控制，一旦系统的各个参数发生改变或者系统受到外界干扰之后，控制系统将失去实效性。而且在选择PID的各个参数时只能通过经验来设定，并没有固定的参考标准，所以对于没经验的学者而言，刚开始设置的PID参数不一定能够很好的控制系统，说不定还会加剧系统的振动。而BP神经网络PID控制通过不断调整参数寻找最优的控制律，最后得出的比例、积分和微分系数也是最优的。同时由于BP神经网络PID控制能够通过系统的参数和设定的参考值不断的修改权值，所以即使系统的某些参数发生了变化，仍然能够达到较好的控制效果。

3 结论

以机床再生型切削颤振为研究对象，并以实际加工中的镗削颤振抑制问题为背景建立了具有连续分布质量的压电智能切削颤振抑制系统动力学模型，最后利用BP神经网络和经典PID相结合的智能控制策略对其进行主动控制。仿真分析结果表明，BP神经网络PID控制能够让颤振抑制系统在较短时间内收敛到平衡位置，因为神经网络通过不断调整参数寻找最优的控制律，最后得出的比例、积分和微分系数也是最优的。同时由于BP神经网络PID控制能够通过系统的参数和设定的参考值不断的修改权值，所以具有很强的抗干扰性，即使系统的各个参数发生了改变，BP神经网络PID控制系统一样能够对其进行有效地控制。

［1］陈花玲.机床切削颤振的非线性理论研究［J］.振动工程学报，1992，5(4):335-342.

［2］于骏一，周晓勤.切削颤振的预报控制［J］.中国机械工程，1999，10(9):43-46.

［3］胡海岩，郭大蕾，翁建生.振动半主动控制技术的进展［J］.振动、测试与诊断，2001，21(4):235-244.

［4］周晓勤，于骏一，王文才.人工神经网络在切削颤振类别诊断中的应用［J］.农业机械学报，1998，29(20):156-160.

［5］孔繁森，刘鹏，刘春颖.基于压电智能结构的镗削振动主动控制的仿真与实验研究［J］.振动与冲击，2010，29(3):142-146.

［6］陈晓宁.基于神经网络振动主动控制方法的研究［D］.哈尔滨:哈尔滨工程大学，2004.

［7］任伟建，杜红嘉，郇启亮，等.神经网络PID控制器在油田标定间上的应用［J］.大庆石油学院学报，2001，25(2):37-39.

［8］李绍铭，赵伟.基于S函数的BP神经网络PID控制器simulink仿真［J］.可编程控制器与工厂自动化，2008(3):95-97.