基于ARM11机床热误差实时补偿器研究

张志鹏，刘康，曾祥兵，刘光磊，郭丰

(1.四川理工学院机械工程学院，四川自贡643000;2.四川长征机床集团有限责任公司，四川自贡643000)

0 前言

随着对数控机床加工精度的要求日益提高，误差补偿技术已经成为提高机床精度的重要方法。几何误差、热误差、力误差是数控机床的3大主要误差，占总误差的70% ～90%［1］，其中在精密加工过程中，热误差占总误差的40% ～70%［2］，越是精密的机床，热误差所占比例越大。因此，进行机床主轴热误差补偿，对提高数控机床加工精度有重要意义。几何误差属于静态误差［3］，经过多年的研究，已经取得了很多成果，热误差属于动态误差，简单的误差补偿器无法随着时间或其他因素的改变而实时在线补偿。通用计算机可以实现一台甚至多台［4］机床的误差补偿，但实现成本较高。嵌入式装置是以应用为中心、软硬件可裁剪的专用计算机，具有成本低、体积小、实时性高和界面友好的特点。随着嵌入式设备应用越来越广泛［5］，嵌入式技术结合机床热误差补偿研究取得了一些的进展［6］，但只是针对某一特定型号机床和在特定环境下进行的热误差补偿研究，适用范围有限。本文作者以ARM11开发板为主体，设计了3个模块，在Fanuc机床上进行了实验，使用机床提供的外部机械原点偏移［7］功能，对Fanuc机床主轴热误差实时在线补偿研究。

1 温度采集分析模块

该模块主要功能是优化温度关键点，确定关键点后进行实时补偿，利用串口一将温度值送给OK6410A开发板。通过对KVC650E立式加工中心的结构特点和热源分布进行分析和初步试验，在床身上对影响主轴热误差较大的位置分布了温度传感器，将数据采集到PC机上，进行优化分析，温度变量的优化选择过程，其优化过程如下:

(1)根据机床分析和基本原则初步布置测温点;对温度变量进行模糊聚类，通过计算F统计量优选阈值来确定最佳分组;

(2)对各温度变量与热误差数据进行灰色综合关联分析，选取各组中与热误差灰色综合关联度最大的温度变量，并考虑所选温度变量是否满足实际情况和条件，若满足，最终确定用于热误差建模的温度变量，若不满足，返回重选阈值。

(3)确定温度关键点，温度采集模块一如图1所示。

图1 温度采集分析模块

通过温度关键点优化，可以消除温度测点之间的相互耦合作用，增强热误差模型的鲁棒性，而且还能减少温度数据的检测数量和简化模型的复杂度。温度采集模块的硬件包括STC90C51RD芯片和带有1602液晶显示器的单片机，OK6410A实时显示温度传感器数值，8路DS18B20温度传感器。经过模块化的设计，若要改变温度传感器的数目，单片机程序只需根据不同的温度传感器序列号，增减相应的程序，并在计算机上进行相关的优化分析。

2 热误差建模及实时补偿模块

2.1 建模理论

热误差建模是热误差补偿研究的关键技术，模型的预测精度直接影响到热误差补偿系统的补偿效果，国内外学者进行了大量研究，多元线性回归 (MLR，Multiple Linear Regression)是行之有效的快速建模方法之一［8-9］。在不同的机床类型和不同的时间内，每种建模都有各自的适应范围，模型大多不同，开发板的存储空间比较大，并且可以扩展存储空间，这就为保存多个模型数据提供了条件。为了验证补偿器的可行性，首先将多元线性回归算法移植到开发板，然后选择具有更好补偿效果的模型。多元线性回归基于最小二乘原理，以因变量与自变量之间成线性关系的假设为基础，通过实验，得到多个测温点温度与机床单个方向上的热误差变化输出关系。假设模型中热误差(因变量)Z与 m个温度测点 (自变量)T1，T2，…，Tm存在线性的内在联系，通过实验每个温度测点得到n组数据:T1k，T2k，…，Tmk，k＝1，2，…，n，则可得到如下关系式:

多元线性回归模型关系式为:Z＝TC＋μ

其中:式中:Zi为机床某一方向第i次测得的热误差值;Ci为回归系数;Tki为机床上第k个传感器第i次测得的温度;μi为相互独立且服从同一正态分布的随机变量;Z与T为已知参数，利用最小二乘法可以求出计算参数C。

设c0，c1，…，cm分别为参数 C0，C1，…，Cm的最小二乘估计，则多元线性回归方程为:

2.2 硬件资源

(1)SamsungS3C6410处理器，ARM1176JZF-S内核，主频533 MHz/667 MHz;

(2)128M字节Mobile DDR内存;(3)1G字节NAND Flash(MLC);(4)12 MHz、48 MHz、27 MHz、32.768 kHz 时钟源;

(5)内部实时钟，带有后备锂电池座，断电后系统时间不丢失;

(6)共4个串口，包括1个五线RS232电平串口和3个三线TTL电平串口及扩展RS232串口;

(7)1个USB HOST插口，支持USB1.1，可插鼠标、U盘等;

(8)1个100M网口，采用DM9000AE，带连接和传输指示灯;

(9)3.5寸 LCD，支持 TFT LCD，支持10寸LVDS液晶屏;

(10)核心板为6层PCB设计，性能稳定，经过强电磁环境考验。

以上的硬件资源表明:OK6410开发板为机床主轴热误差实时补偿研究提供了良好的平台。

2.3 系统平台的搭建

系统平台的搭建是实现一个信息处理终端，为OK6410A开发板搭建Linux系统，包括以下4个部分［10-11］:

(1)引导装载程序 (BootLoader)，这里选用uboot1.1.6版，系统上电后首先被执行，对CPU、内存等进行初始化，完成内核映像的装载和引导;

(2)Linux内核，采用官方的Linux3.0.1版本，配置编译后生成zImage内核映像文件，并制作yaffs2文件系统映像，利用SD卡一键安装Linux系统;

(3)图形用户界面，Qtopia是Trolltech公司为采用嵌入式Linux操作系统的消费电子设备而开发的综合应用平台，选用功能强大且实用的Qtopia2.2.0版本。

(4)在Qtcreator软件中编写并交叉编译应用程序，QT体系开发模型如图2所示。

图2 QT的体系开发模型

2.4 软件设计

软件设计主要在Linux系统下完成，虚拟机选用VMware Workstation10，系统使用Ubuntu 12.04版本，安装QtCreator4.8.1后，即可编写QT程序，主要是基于QT下的热误差建模编程、通信编程和应用程序的交叉编译及移植［1-2］，同时还需在开发板上设置环境变量，可以利用触摸笔打开程序或在开发板上设置开机启动热误差补偿程序，点击“开始补偿”按钮后，便可以进行热误差补偿，开发流程如图3所示。

图3 QT开发流程图

为了增强该模块的通用性，机床类型包含Fanuc和Siemens 2类机床，误差补偿类型设计了几何误差、热误差、切削力误差和综合误差模型算法，模型包括:经典的多元线性回归算法、应用广泛且具有较强鲁棒性和容错性的BP神经网络［13］。经过移植QT程序，开发板具有良好的人机交互界面，便于观察传感器温度值和X、Y、Z三轴的补偿量。设计的图形用户界面 (GUI，Graphic User Interface)如图4所示。

图4 GUI界面结构图

3 机床接收数据模块

经分析配置Fanuc 0i Mate-MC系统的 KVC650E立式加工中心和配置Siemens 840D系统的GMC4000H/2龙门加工中心的通信接口，分别制定了两种通信补偿方案:西门子机床需要解决的是内嵌式S7-300PLC与ARM11以太网通信，是基于QT下的Socket通信［5］。文中主要介绍Fanuc 0i Mate-MC系统KVC650E立式加工中心的通信接口，经查阅资料，利用扩展板将X输入开关量信号与串口控制器进行点对点连接，ARM11经串口二送出的误差值送给X地址，根据机床功能手册，在LADDER3软件编写对应的读取外部数据部分梯形图，利用M-Card将梯形图与机床进行梯形图转换，模块设计流程如图5所示。

图5 模块三流程图

4 热误差实时补偿实验

为了验证该补偿器的可行性及补偿效果，以多元线性回归算法建立数学模型，以主轴轴向为例，在KVC650E立式加工中心上进行实验，整个过程流程如图6所示。

图6 整体流程图

将采集8路温度数据及检测Z轴轴向热变形值采集到电脑上进行分析，利用MATLAB数学工具，得到各温度传感器的变化曲线如图7所示，主轴热变形曲线如图8所示。

图7 各温度传感器的温度变化曲线

图8 主轴轴向热变形曲线

首先计算出各温度变量间的相关系数矩阵R，然后计算R的传递包t(R)，得到模糊等价矩阵，借助F统计量对温度变量进行分组，经分析取阈值λ＝0.987，此时8个温度变量共分为4组，分组结果如表1所示。

表1 温度变量的分组

根据灰色综合关联度分析，由两序列间的灰色综合关联度定义

分别计算出各温度变量与主轴轴向热误差的灰色综合关联系数。按灰色综合关联系数大小进行排序，如表2所示。

根据模糊聚类的分组结果，从每组中选择温度测点数据与热误差灰色综合关联最大的值，则应选择T1、T2、T6、T8作为温度关键点。通过表2，最终确定T2、T6、T8作为温度关键点，为了减小了模型复杂度，提升模型的精确性和鲁棒性，采用实时相对温度作为自变量，建立热误差补偿模型，确定多元线性回归公式为:

利用MATLAB工具分析热误差测量值、MLR模型预测值及残差，结果如图9所示。

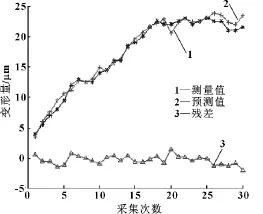
图9 MLR补偿误差

图9 中模型的最大残差绝对值为2.687 8μm。计算残差均方根为S＝1.245 1μm。

图10为热误差补偿实验现场，可以在机床的显示屏上看到传入的G地址数据，利用千分表测量机床轴向位移随着数据的改变而移动，从而证明了补偿器的可行性。

图10 热误差补偿实验现场

利用千分表测量主轴轴向热误差，补偿预测值和实际测得Z轴变形量如图11所示，经过热误差实时补偿实验，误差值控制在-10～4μm范围内，轴向热误差从补偿前的24μm降低到14μm，补偿效果达到40%，从而证明了该补偿器能够取得良好的补偿精度。

图11 实验对比热误差补偿效果图

5 结论

(1)介绍了一种基于ARM11机床热误差补偿器，将多元线性回归预测模型嵌入到补偿器中，在KVC650E立式加工中心上实验，证明了该补偿器的可行性及良好的补偿效果。

(2)实验表明，采用多元线性回归建模的方法，能够达到一定的补偿效果。为了进一步提高误差控制精度，可以根据实验情况将几个线性回归模型适当组合或补偿器中嵌入预测效果更好的模型，比如神经网络模型，将误差控制在更小的范围内。

(3)该补偿器具有成本低、实时性高、通用性强的特点，随着研究不断的完善，能够进一步开发成商业产品。因此，该补偿器的研究具有重要参考价值和实际意义。

［1］张宏韬.双转台五轴数控机床误差的动态实时补偿研究［D］.上海:上海交通大学，2011.

［2］BRYAN J.International Status of Thermal Error Research［J］.Annals of the CIRP，1990，39(2):645-656.

［3］曹永洁.基于激光测试技术的数控机床误差辨识与补偿研究［D］.杭州:浙江大学，2006.

［4］张毅.数控机床误差测量、建模及网络群控实时补偿系统研究［D］.上海:上海交通大学，2013.

［5］时岩.嵌入式技术发展状况综述［J］.电子技术，2012(5):4-5.

［6］任兵，任小红，徐卫东，等.基于ARM_Linux的数控机床热误差补偿控制器设计［J］.组合机床与自动化加工技术，2010(4):25-31.

［7］任永强，杨建国，罗磊等.基于外部机床坐标系偏移的热误差实时补偿［J］.中国机械工程，2003，14(14):1243-1246.

［8］RAMESH R，MANNAN M A.Error Compensation in Machine Tools a Review(Part II):Thermal Errors.International［J］.Journal of Machine Tool ＆ Manufacture，2000，40(9):1257-1284.

［9］YUAN J，NI J.The real-time Error Compensation Technique for CNC Machining Systems［J］.Mechatronics，1998，8(4):359-380.

［10］飞凌嵌入式.《OK6410 QT移植百科全书》［EB/OL］.［2014-1］.www.witech.com.cn.

［11］张霄.基于ARM11的嵌入式linux系统移植与实现［D］.济南:山东大学，2013.

［12］蔡志明，卢传富，李立夏.精通QT4编程［M］.2版.北京:电子工业出版社，2008.

［13］王健伟，宋执环.基于嵌入式系统的神经网络在线训练平台实现［J］.传感器与微系统，2010，29(8):100-103.